Toán 8 Bài 6 (Kết nối tri thức): Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

Với giải bài tập Toán lớp 8 Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 6.

1 5,872 20/09/2024

Trang trước

Trang sau

Giải Toán 8 Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

Bài giảng Toán 8 Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu - Kết nối tri thức

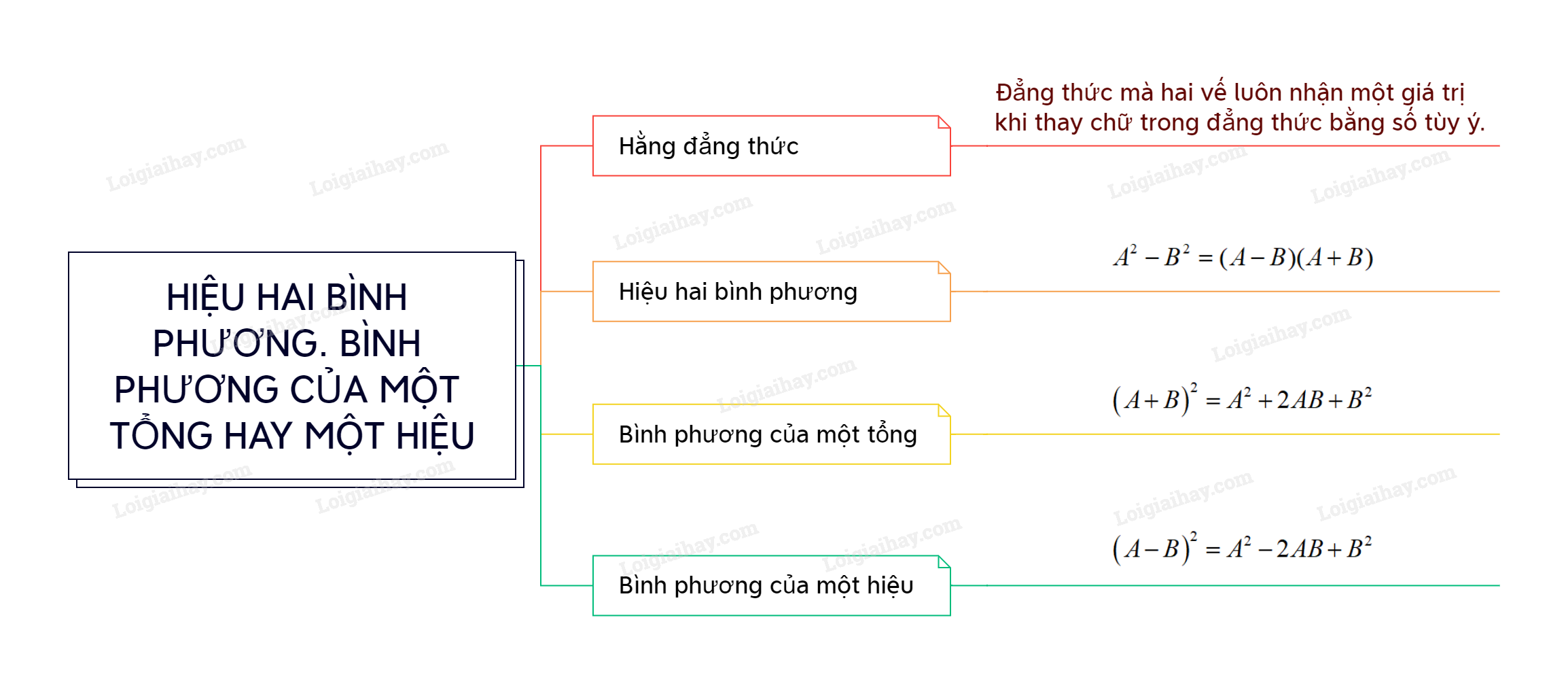
1. Hằng đẳng thức

Giải Toán 8 trang 30

Luyện tập 1 trang 30 Toán 8 Tập 1: Trong các đẳng thức sau, đẳng thức nào là hằng đẳng thức?

a) $a (a + 2 b) = a^{2} + 2 a b$

b) $a + 1 = 3 a - 1$

Phương pháp giải:

Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.

Lời giải:

a) $a (a + 2 b) = a^{2} + 2 a b$ là hằng đẳng thức.

b) $a + 1 = 3 a - 1$ không là hằng đẳng thức vì khi ta thay $a = 2$ thì hai vế của đẳng thức không bằng nhau.

2. Hiệu hai bình phương

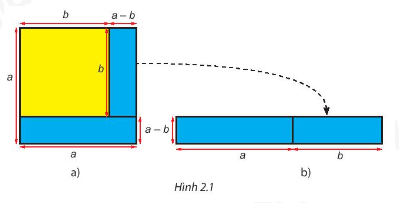
HĐ 1 trang 30 Toán 8 Tập 1: Quan sát Hình 2.1

a) Tính diện tích của phần hình màu xanh ở Hình 2.1a.

b) Tính diện tích hình chữ nhật màu xanh ở Hình 2.1b.

c) Có nhận xét gì về diện tích của hai hình ở câu a và câu b?

Phương pháp giải:

Diện tích hình chữ nhật = chiều dài . chiều rộng

Lời giải:

a) Diện tích của phần hình màu xanh ở Hình 2.1a là: $a^{2} - b^{2}$ .

b) Diện tích hình chữ nhật màu xanh ở Hình 2.1b là: $(a + b) (a - b)$ .

c) Diện tích hai hình ở câu a và b bằng nhau.

Giải Toán 8 trang 31

HĐ 2 trang 31 Toán 8 Tập 1: Với hai số a,b bất kì, thực hiện phép tính $(a + b) (a - b)$ .

Từ đó rút ra liên hệ giữa $a^{2} - b^{2}$ và $(a + b) (a - b)$ .

Phương pháp giải:

Muốn nhân hai đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả với nhau.

Lời giải:

$(a + b) (a - b) = a . a - a b + b . a - b . b = a^{2} - b^{2} + (- a b + b a) = a^{2} - b^{2}$

Từ đó ta được $a^{2} - b^{2} = (a + b) (a - b)$

Luyện tập 2 trang 31 Toán 8 Tập 1: a) Tính nhanh $99^{2} - 1$

b) Viết $x^{2} - 9$ dưới dạng tích.

Phương pháp giải:

Sử dụng hằng đẳng thức $a^{2} - b^{2} = (a + b) (a - b)$

Lời giải:

a) $99^{2} - 1 = 99^{2} - 1^{2} = (99 + 1) . (99 - 1) = 100.98 = 9800.$

b) $x^{2} - 9 = x^{2} - 3^{2} = (x + 3) . (x - 3)$

Vận dụng trang 31 Toán 8 Tập 1: Ở bài toán mở đầu, em hãy giải thích xem bạn đó tính nhanh như thế nào.

Phương pháp giải:

Sử dụng hằng đẳng thức $a^{2} - b^{2} = (a + b) (a - b)$

Lời giải:

$198.202 = (200 - 2) . (200 + 2) = 200^{2} - 2^{2} = 400 - 4 = 396.$

3. Bình phương của một tổng

HĐ 3 trang 31 Toán 8 Tập 1: Với hai số a,b bất kì, thực hiện phép tính $(a + b) . (a + b)$ .

Từ đó rút ra liên hệ giữa ${(a + b)}^{2}$ và $a^{2} + 2 a b + b^{2}$

Phương pháp giải:

Muốn nhân hai đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả với nhau.

Lời giải:

$(a + b) . (a + b) = a . a + a . b + b . a + b . b = a^{2} + (a b + a b) + b^{2} = a^{2} + 2 a b + b^{2}$

Từ đó ta được ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Giải Toán 8 trang 32

Luyện tập 3 trang 32 Toán 8 Tập 1: 1. Khai triển ${(2 b + 1)}^{2}$

2. Viết biểu thức $9 y^{2} + 6 y x + x^{2}$ dưới dạng bình phương của một tổng.

Phương pháp giải:

Sử dụng hằng đẳng thức ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Lời giải:

1. ${(2 b + 1)}^{2} = {(2 b)}^{2} + 2.2 b .1 + 1^{2} = 4 b^{2} + 4 b + 1$

2. $9 y^{2} + 6 y x + x^{2} = {(3 y)}^{2} + 2.3 y . x + x^{2} = {(3 y + x)}^{2}$

4. Bình phương của một hiệu

HĐ 4 trang 32 Toán 8 Tập 1: Với hai số a, b bất kì, viết $a - b = a + (- b)$ và áp dụng hằng đẳng thức bình phương của một tổng để tính ${(a - b)}^{2}$ .

Phương pháp giải:

Sử dụng hằng đẳng thức ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Lời giải:

${(a - b)}^{2} = {[a + (- b)]}^{2} = a^{2} + 2. a . (- b) + {(- b)}^{2} = a^{2} - 2. a b + b^{2}$

Luyện tập 4 trang 32 Toán 8 Tập 1: Khai triển ${(3 x - 2 y)}^{2}$

Phương pháp giải:

Sử dụng hằng đẳng thức ${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Lời giải:

${(3 x - 2 y)}^{2} = {(3 x)}^{2} - 2.3 x .2 y + {(2 y)}^{2} = 9 x^{2} - 12 x y + 4 y^{2}$

Vận dụng trang 32 Toán 8 Tập 1: Trong trò chơi “Ai thông minh hơn học sinh lớp 8”, người dẫn chương trình yêu cầu các bạn học sinh cho biết kết quả của phép tính $1002^{2}$ . Chỉ vài giây sau, Nam đã tính ra kết quả chính xác và giành được điểm. Em hãy giải thích xem Nam đã tính nhanh như thế nào.

Phương pháp giải:

Sử dụng hằng đẳng thức ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Lời giải:

$1002^{2} = {(1000 + 2)}^{2} = 1000^{2} + 2.1000.2 + 2^{2} = 1000000 + 4000 + 4 = 1004004$

Bài tập

Giải Toán 8 trang 33

Bài 2.1 trang 33 Toán 8 Tập 1: Những đẳng thức nào sau đây là hằng đẳng thức?

a) $x + 2 = 3 x + 1$

b) $2 x (x + 1) = 2 x^{2} + 2 x$

c) $(a + b) a = a^{2} + b a$

d) $a - 2 = 2 a + 1$

Phương pháp giải

Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.

Lời giải:

a) $x + 2 = 3 x + 1$ không là hằng đẳng thức vì khi ta thay $x = 0$ thì hai vế của đẳng thức không bằng nhau.

b) $2 x (x + 1) = 2 x^{2} + 2 x$ là hằng đẳng thức.

c) $(a + b) a = a^{2} + b a$ là hằng đẳng thức.

d) $a - 2 = 2 a + 1$ không là hằng đẳng thức vì khi ta thay $a = 0$ thì hai vế của đẳng thức không bằng nhau.

Bài 2.2 trang 33 Toán 8 Tập 1: Thay bằng biểu thức thích hợp.

a) $(x - 3 y) (x + 3 y) = x^{2} - ?$ ;

b) $(2 x - y) (2 x + y) = 4 ? - y^{2}$ ;

c) $x^{2} + 8 x y + ? = {(? + 4 y)}^{2}$ ;

d) $? - 12 x y + 9 y^{2} = {(2 x - ?)}^{2}$ .

Phương pháp giải

Sử dụng ba hằng đẳng thức:

$\begin{array}{l} +) A^{2} - B^{2} = (A + B) (A - B) \\ +) {(A + B)}^{2} = A^{2} + 2 A B + B^{2} \\ +) {(A - B)}^{2} = A^{2} - 2 A B + B^{2} \end{array}$

Lời giải:

a) $(x - 3 y) (x + 3 y) = x^{2} - 9 y^{2}$ ;

b) $(2 x - y) (2 x + y) = 4 x^{2} - y^{2}$ ;

c) $x^{2} + 8 x y + 16 y^{2} = {(x + 4 y)}^{2}$ ;

d) $4 x^{2} - 12 x y + 9 y^{2} = {(2 x - 3 y)}^{2}$ .

Bài 2.3 trang 33 Toán 8 Tập 1: Tính nhanh:

a) $54.66$ ;

b) $203^{2}$ .

Phương pháp giải

Sử dụng 2 hằng đẳng thức:

$\begin{array}{l} +) A^{2} - B^{2} = (A + B) (A - B) \\ +) {(A + B)}^{2} = A^{2} + 2 A B + B^{2} \end{array}$

Lời giải:

a) $54.66 = (60 - 6) . (60 + 6) = 60^{2} - 6^{2} = 3600 - 36 = 3564$

b) $203^{2} = {(200 + 3)}^{2} = 200^{2} + 2.200.3 + 3^{2} = 40000 + 600 + 9 = 40609$

Bài 2.4 trang 33 Toán 8 Tập 1: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) $x^{2} + 4 x + 4$

b) $16 a^{2} - 16 a b + 4 b^{2}$

Phương pháp giải

Sử dụng 2 hằng đẳng thức:

$\begin{array}{l} +) {(A + B)}^{2} = A^{2} + 2 A B + B^{2} \\ +) {(A - B)}^{2} = A^{2} - 2 A B + B^{2} \end{array}$

Lời giải:

a) $x^{2} + 4 x + 4 = x^{2} + 2. x .2 + 2^{2} = {(x + 2)}^{2}$

b) $16 a^{2} - 16 a b + 4 b^{2} = {(4 a)}^{2} - 2.4 a .2 b + {(2 b)}^{2} = {(4 a - 2 b)}^{2}$

Bài 2.5 trang 33 Toán 8 Tập 1: Rút gọn các biểu thức sau:

a) ${(x - 3 y)}^{2} - {(x + 3 y)}^{2}$

b) ${(3 x + 4 y)}^{2} + {(4 x - 3 y)}^{2}$

Phương pháp giải

Sử dụng ba hằng đẳng thức:

$\begin{array}{l} +) A^{2} - B^{2} = (A + B) (A - B) \\ +) {(A + B)}^{2} = A^{2} + 2 A B + B^{2} \\ +) {(A - B)}^{2} = A^{2} - 2 A B + B^{2} \end{array}$

Lời giải:

${(x - 3 y)}^{2} - {(x + 3 y)}^{2} = (x - 3 y + x + 3 y) . (x - 3 y - x - 3 y) = (2 x) . (- 6 y) = - 12 x y$

$\begin{array}{l} {(3 x + 4 y)}^{2} + {(4 x - 3 y)}^{2} \\ = {(3 x)}^{2} + 2.3 x .4 y + {(4 y)}^{2} + {(4 x)}^{2} - 2.4 x .3 y + {(3 y)}^{2} \\ = 9 x^{2} + 24 x y + 16 y^{2} + 16 x^{2} - 24 x y + 9 y^{2} \\ = (9 x^{2} + 16 x^{2}) + (24 x y - 24 x y) + (16 y^{2} + 9 y^{2}) \\ = 25 x^{2} + 25 y^{2} \end{array}$

Bài 2.6 trang 33 Toán 8 Tập 1: Chứng minh rằng với mọi số tự nhiên n, ta có: ${(n + 2)}^{2} - n^{2}$ chia hết cho 4.

Phương pháp giải

Sử dụng hằng đẳng thức $a^{2} - b^{2} = (a + b) (a - b)$

Nếu 2 số nguyên a, b thỏa mãn a chia hết cho 4 thì a.b chia hết cho 4.

Lời giải:

Ta có:

${(n + 2)}^{2} - n^{2} = (n + 2 - n) . (n + 2 + n) = 2. (2 n + 2) = 2.2. (n + 1) = 4. (n + 1)$

Vì $4 ⋮ 4$ nên $4 (n + 1) ⋮ 4$ với mọi số tự nhiên n.

Lý thuyết Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

1. Hằng đẳng thức

Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.

Ví dụ: $a + b = b + a; a (a + 2) = a^{2} + 2 a$ là những hằng đẳng thức.

$a^{2} - 1 = 3 a; a (a - 1) = 2 a$ không phải là những hằng đẳng thức.

2. Hiệu hai bình phương

Hiệu hai bình phương là gì?

$A^{2} - B^{2} = (A - B) (A + B)$

Ví dụ: $101^{2} - 99^{2} = (101 - 99) (101 + 99) = 2.200 = 400$

3. Bình phương của một tổng

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Ví dụ: $101^{2} = (100 + 1)^{2} = 100^{2} + 2.100.1 + 1^{2} = 10201$

4. Bình phương của một hiệu

${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Ví dụ: $99^{2} = (100 - 1)^{2} = 100^{2} - 2.100.1 + 1^{2} = 9801$

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 7: Lập phương của một tổng. Lập phương của một hiệu

Bài 8: Tổng và hiệu hai lập phương

Luyện tập chung trang 40

Bài 9: Phân tích đa thức thành nhân tử

Luyện tập chung trang 45

1 5,872 20/09/2024

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3