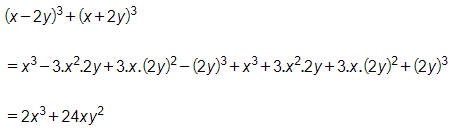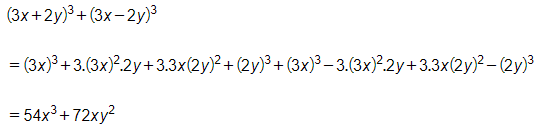Toán 8 Bài 7 (Kết nối tri thức): Lập phương của một tổng. Lập phương của một hiệu

Với giải bài tập Toán lớp 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 7.

1 6,035 20/09/2024

Trang trước

Trang sau

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu

Bài giảng Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

1. Lập phương của một tổng

Giải Toán 8 trang 34

HĐ 1 trang 34 Toán 8 Tập 1: Với hai số a,b bất kì, thực hiện phép tính

$(a + b) {(a + b)}^{2}$

Từ đó rút ra liên hệ giữa ${(a + b)}^{3}$ và $a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ .

Phương pháp giải:

Muốn nhân hai đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả với nhau.

Sử dụng hằng đẳng thức ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Lời giải:

$\begin{array}{l} (a + b) {(a + b)}^{2} = (a + b) . (a^{2} + 2 a b + b^{2}) \\ = a . a^{2} + a .2 a b + a . b^{2} + b . a^{2} + b .2 a b + b . b^{2} \\ = a^{3} + 2 a^{2} b + a b^{2} + a^{2} b + 2 a b^{2} + b^{3} \\ = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} \end{array}$

Giải Toán 8 trang 35

Luyện tập 1 trang 35 Toán 8 Tập 1: 1. Khai triển:

a) ${(x + 3)}^{3}$

b) ${(x + 2 y)}^{3}$

2. Rút gọn biểu thức ${(2 x + y)}^{3} - 8 x^{3} - y^{3}$

Phương pháp giải:

Sử dụng hằng đẳng thức ${(A + B)}^{3} = A^{3} + 3 A^{2} B + 3 A B^{2} + B^{3}$

Lời giải:

1. a)

${(x + 3)}^{3} = x^{3} + 3. x^{2} .3 + 3. x {.3}^{2} + 3^{3} = x^{3} + 9 x^{2} + 27 x + 27$

${(x + 2 y)}^{3} = x^{3} + 3. x^{2} .2 y + 3. x . {(3 y)}^{2} + {(3 y)}^{3} = x^{3} + 6 x^{2} y + 27 x y^{2} + 27 y^{3}$

$\begin{array}{l} {(2 x + y)}^{3} - 8 x^{3} - y^{3} \\ = {(2 x)}^{3} + 3. {(2 x)}^{2} . y + 3.2 x . y^{2} + y^{3} - 8 x^{3} - y^{3} \\ = 8 x^{2} + 12 x^{2} y + 6 x y^{2} + y^{3} - 8 x^{3} - y^{3} \\ = (8 x^{2} - 8 x^{2}) + 12 x^{2} y + 6 x y^{2} + (y^{3} - y^{3}) \\ = 12 x^{2} y + 6 x y^{2} \end{array}$

Luyện tập 2 trang 35 Toán 8 Tập 1: Viết biểu thức $x^{3} + 9 x^{2} y + 27 x y^{2} + 27 y^{3}$ dưới dạng lập phương của một tổng.

Phương pháp giải:

Sử dụng hằng đẳng thức ${(A + B)}^{3} = A^{3} + 3 A^{2} B + 3 A B^{2} + B^{3}$

Lời giải:

$\begin{array}{l} x^{3} + 9 x^{2} y + 27 x y^{2} + 27 y^{3} \\ = x^{3} + 3. x^{2} .3 y + 3. x . {(3 y)}^{2} + {(3 y)}^{3} \\ = {(x + 3 y)}^{3} \end{array}$

2. Lập phương của một hiệu

HĐ 2 trang 35 Toán 8 Tập 1: Với hai số $a, b$ bất kì, viết $a - b = a + (- b)$ và áp dụng hằng đẳng thức lập phương của một tổng để tính ${(a - b)}^{3}$ .

Từ đó rút ra liên hệ giữa ${(a - b)}^{3}$ và $a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}$ .

Phương pháp giải:

Sử dụng hằng đẳng thức ${(A + B)}^{3} = A^{3} + 3 A^{2} B + 3 A B^{2} + B^{3}$

Lời giải:

${(a - b)}^{3} = {[a + (- b)]}^{3} = a^{3} + 3. a^{2} . (- b) + 3. a . {(- b)}^{2} + {(- b)}^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}$

Từ đó ta có ${(a - b)}^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}$

Luyện tập 3 trang 35 Toán 8 Tập 1: Khai triển ${(2 x - y)}^{3}$

Phương pháp giải:

Sử dụng hằng đẳng thức ${(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3}$

Lời giải:

${(2 x - y)}^{3} = {(2 x)}^{3} - 3. {(2 x)}^{2} . y + 3.2 x . y^{2} - y^{3} = 8 x^{3} - 12 x^{2} y + 6 x y^{2} - y^{3}$

Giải Toán 8 trang 36

Luyện tập 4 trang 36 Toán 8 Tập 1: Viết biểu thức sau dưới dạng lập phương của một hiệu

$8 x^{3} - 36 x^{2} y + 54 x y^{2} - 27 y^{3}$ .

Phương pháp giải:

Sử dụng hằng đẳng thức ${(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3}$

Lời giải:

$\begin{array}{l} 8 x^{3} - 36 x^{2} y + 54 x y^{2} - 27 y^{3} \\ = {(2 x)}^{3} - 3. {(2 x)}^{2} .3 y + 3. (2 x) . {(3 y)}^{2} - {(3 y)}^{3} \\ = {(2 x - 3 y)}^{3} \end{array}$

Vận dụng trang 36 Toán 8 Tập 1: Rút gọn biểu thức

${(x - y)}^{3} + {(x + y)}^{3}$ .

Phương pháp giải:

Sử dụng 2 hằng đẳng thức:

$\begin{array}{l} +) {(A + B)}^{3} = A^{3} + 3 A^{2} B + 3 A B^{2} + B^{3} \\ +) {(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3} \end{array}$

Lời giải:

$\begin{array}{l} {(x - y)}^{3} + {(x + y)}^{3} = x^{3} - 3 x^{2} y + 3 x y^{2} - y^{3} + x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3} \\ = (x^{3} + x^{3}) + (- 3 x^{2} y + 3 x^{2} y) + (3 x y^{2} + 3 x y^{2}) + (- y^{3} + y^{3}) \\ = 2 x^{3} + 6 x y^{2} \end{array}$

Bài tập

Bài 2.7 trang 36 Toán 8 Tập 1: Khai triển:

a) ${(x^{2} + 2 y)}^{3}$ ;

b) ${(\frac{1}{2} x - 1)}^{3}$ .

Phương pháp giải

$\begin{array}{l} {(x^{2} + 2 y)}^{3} = {(x^{2})}^{3} + 3. {(x^{2})}^{2} .2 y + 3. x^{2} . {(2 y)}^{2} + {(2 y)}^{3} \\ = x^{6} + 6 x^{4} y + 12 x^{2} y^{2} + 8 y^{3} \end{array}$

${(\frac{1}{2} x - 1)}^{3} = {(\frac{1}{2} x)}^{3} - 3. {(\frac{1}{2} x)}^{2} .1 + 3. \frac{1}{2} x {.1}^{2} - 1^{3} = \frac{1}{8} x^{3} - \frac{3}{4} x^{2} + \frac{3}{2} x - 1$

Lời giải:

$\begin{array}{l} {(x^{2} + 2 y)}^{3} = {(x^{2})}^{3} + 3. {(x^{2})}^{2} .2 y + 3. x^{2} . {(2 y)}^{2} + {(2 y)}^{3} \\ = x^{6} + 6 x^{4} y + 12 x^{2} y^{2} + 8 y^{3} \end{array}$

${(\frac{1}{2} x - 1)}^{3} = {(\frac{1}{2} x)}^{3} - 3. {(\frac{1}{2} x)}^{2} .1 + 3. \frac{1}{2} x {.1}^{2} - 1^{3} = \frac{1}{8} x^{3} - \frac{3}{4} x^{2} + \frac{3}{2} x - 1$

Bài 2.8 trang 36 Toán 8 Tập 1: Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu.

a) $27 + 54 x + 36 x^{2} + 8 x^{3}$ .

b) $64 x^{3} - 144 x^{2} y + 108 x y^{2} - 27 y^{3}$ .

Phương pháp giải

a) $27 + 54 x + 36 x^{2} + 8 x^{3} = 3^{3} + {3.3}^{2} .2 x + 3.3. {(2 x)}^{2} + {(2 x)}^{3} = {(3 + 2 x)}^{3}$

$64 x^{3} - 144 x^{2} y + 108 x y^{2} - 27 y^{3} = {(4 x)}^{3} - 3. {(4 x)}^{2} .3 y + 3.4 x . {(3 y)}^{2} - {(3 y)}^{3} = {(4 x - 3 y)}^{3}$

Lời giải:

a) $27 + 54 x + 36 x^{2} + 8 x^{3} = 3^{3} + {3.3}^{2} .2 x + 3.3. {(2 x)}^{2} + {(2 x)}^{3} = {(3 + 2 x)}^{3}$

$64 x^{3} - 144 x^{2} y + 108 x y^{2} - 27 y^{3} = {(4 x)}^{3} - 3. {(4 x)}^{2} .3 y + 3.4 x . {(3 y)}^{2} - {(3 y)}^{3} = {(4 x - 3 y)}^{3}$

Bài 2.9 trang 36 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức:

a) $x^{3} + 9 x^{2} + 27 x + 27$ tại x=7.

b) $27 - 54 x + 36 x^{2} - 8 x^{3}$ tại x=6,5.

Phương pháp giải

a) $x^{3} + 9 x^{2} + 27 x + 27 = x^{3} + 3. x^{2} .3 + 3. x {.3}^{2} + 3^{3} = {(x + 3)}^{3}$

Thay x=7 vào biểu thức ta được: ${(7 + 3)}^{3} = 10^{3} = 1000$ .

b) $27 - 54 x + 36 x^{2} - 8 x^{3} = 3^{3} - {3.3}^{2} .2 x + 3.3. {(2 x)}^{2} - {(2 x)}^{3} = {(3 - 2 x)}^{3}$

Thay x=6,5 vào biểu thức ta được: ${(3 - 2.6, 5)}^{3} = {(- 10)}^{3} = - 1000$ .

Lời giải:

a) $x^{3} + 9 x^{2} + 27 x + 27 = x^{3} + 3. x^{2} .3 + 3. x {.3}^{2} + 3^{3} = {(x + 3)}^{3}$

Thay x=7 vào biểu thức ta được: ${(7 + 3)}^{3} = 10^{3} = 1000$ .

b) $27 - 54 x + 36 x^{2} - 8 x^{3} = 3^{3} - {3.3}^{2} .2 x + 3.3. {(2 x)}^{2} - {(2 x)}^{3} = {(3 - 2 x)}^{3}$

Thay x=6,5 vào biểu thức ta được: ${(3 - 2.6, 5)}^{3} = {(- 10)}^{3} = - 1000$ .

Bài 2.10 trang 36 Toán 8 Tập 1: Rút gọn các biểu thức sau:

a) ${(x - 2 y)}^{3} + {(x + 2 y)}^{3}$

b) ${(3 x + 2 y)}^{3} + {(3 x - 2 y)}^{3}$

Phương pháp giải

Lời giải:

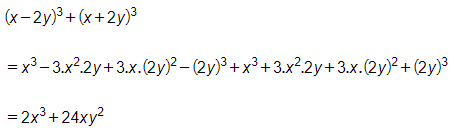
Toán 8 Bài 7 (Kết nối tri thức): Lập phương của một tổng. Lập phương của một hiệu (ảnh 1)

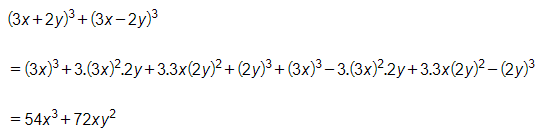
Bài 2.11 trang 36 Toán 8 Tập 1: Chứng minh ${(a - b)}^{3} = - {(b - a)}^{3}$

Phương pháp giải

$\begin{array}{l} {(a - b)}^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} \\ - {(b - a)}^{3} = - (b^{3} - 3 b^{2} a + 3 b a^{2} - a^{3}) \\ = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} \end{array}$

Vậy ${(a - b)}^{3} = - {(b - a)}^{3}$ (đpcm).

Lời giải:

$\begin{array}{l} {(a - b)}^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} \\ - {(b - a)}^{3} = - (b^{3} - 3 b^{2} a + 3 b a^{2} - a^{3}) \\ = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} \end{array}$

Vậy ${(a - b)}^{3} = - {(b - a)}^{3}$ (đpcm).

Lý thuyết Lập phương của một tổng. Lập phương của một hiệu

Lập phương của một tổng:

${(A + B)}^{3} = A^{3} + 3 A^{2} B + 3 A B^{2} + B^{3}$

Ví dụ: ${(x + 3)}^{3} = x^{3} + 3 x^{2} .3 + 3 x {.3}^{2} + 3^{3} = x^{3} + 9 x^{2} + 27 x + 27$

Lập phương của một hiệu:

${(A - B)}^{3} = A^{3} - 3 A^{2} B + 3 A B^{2} - B^{3}$

Ví dụ: ${(x - 3)}^{3} = x^{3} - 3 x^{2} .3 + 3 x {.3}^{2} - 3^{3} = x^{3} - 9 x^{2} + 27 x - 27$

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 8: Tổng và hiệu hai lập phương

Luyện tập chung trang 40

Bài 9: Phân tích đa thức thành nhân tử

Luyện tập chung trang 45

Bài tập cuối chương 2

1 6,035 20/09/2024

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3