Toán 8 Bài 15 (Kết nối tri thức): Định lí Thalès trong tam giác
Với giải bài tập Toán lớp 8 Bài 15: Định lí Thalès trong tam giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 15.
Giải Toán 8 Bài 15: Định lí Thalès trong tam giác
Bài giảng Toán 8 Bài 15: Định lí Thalès trong tam giác
Lời giải:
Sau bài học này ta giải quyết được bài toán như sau:
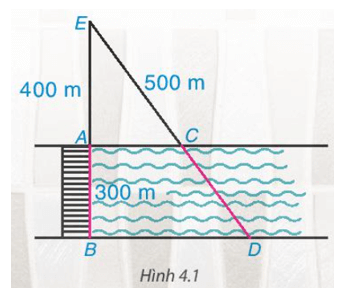
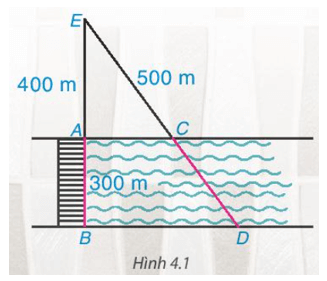
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
AEAB=CECDAEAB=CECD hay 400300=500CD400300=500CD .
Suy ra CD=300 . 500400=375CD=300.500400=375 (m).
Vậy khoảng cách giữa C và D bằng 375 m.
1. Đoạn thẳng tỉ lệ
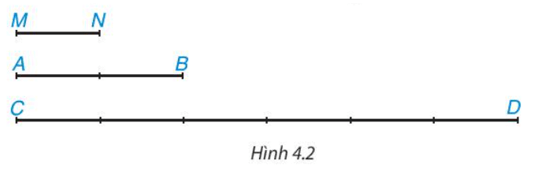
HĐ1 trang 77 Toán 8 Tập 1: Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
Lời giải:
Chọn đoạn MN làm đơn vị độ dài thì MN = 1 (đvđd).
Khi đó, AB = 2 (đvđd); CD = 6 (đvđd).
Do đó ABCD=26=13ABCD=26=13.
Vậy AB = 2 (đvđd); CD = 6 (đvđd); ABCD=13ABCD=13.
HĐ2 trang 77 Toán 8 Tập 1: Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
Lời giải:
Đo độ dài các đoạn thẳng, ta được: AB = 4,8 cm; CD = 14,4 cm.
Khi đó ABCD=4,814,4=13ABCD=4,814,4=13.
HĐ3 trang 77 Toán 8 Tập 1: So sánh hai tỉ số tìm được trong hai hoạt động trên.
Lời giải:
Tỉ số ABCDABCD tìm được ở Hoạt động 1 và Hoạt động 2 bằng nhau và đều bằng 1313.
Luyện tập 1 trang 77 Toán 8 Tập 1: Tính tỉ số của các đoạn thẳng có độ dài như sau:
Lời giải:
a) Tỉ số của các đoạn thẳng được tính như sau: MNPQ=39=13; PQMN=93=31MNPQ=39=13;PQMN=93=31.
Vậy MNPQ=13; PQMN=31MNPQ=13;PQMN=31.
a) Tỉ số của các đoạn thẳng được tính như sau: EFHK=2510=52; HKEF=1025=25EFHK=2510=52;HKEF=1025=25.
Vậy EFHK=52; HKEF=25EFHK=52;HKEF=25.
Dựa vào hình vẽ, hãy tính và so sánh các tỉ số sau và viết các tỉ lệ thức:
b) AB'B'BAB'B'B và AC'C'CAC'C'C .
Lời giải:
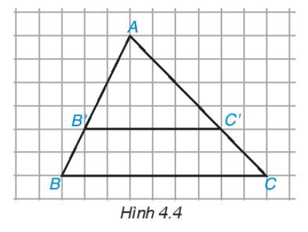
a) Từ hình vẽ ta thấy: AB'AB=46=23; AC'AC=46=23AB'AB=46=23;AC'AC=46=23.
Do đó, AB'AB=AC'ACAB'AB=AC'AC.
b) Từ hình vẽ ta thấy: AB'B'B=42=21; AC'C'C=42=21AB'B'B=42=21;AC'C'C=42=21.
Vậy AB'B'B=AC'C'CAB'B'B=AC'C'C.
c) Từ hình vẽ ta thấy: B'BAB=26=13; C'CAC=62=31B'BAB=26=13;C'CAC=62=31.
Do đó B'BAB=C'CACB'BAB=C'CAC.
2. Định lý Thalès trong tam giác
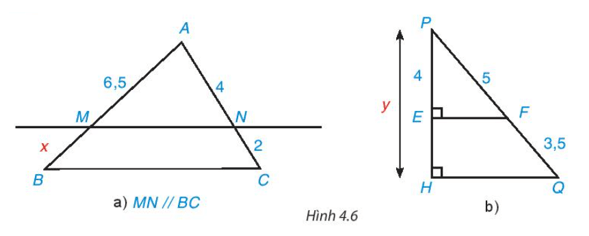
Luyện tập 3 trang 79 Toán 8 Tập 1: Tìm các độ dài x, y trong Hình 4.6.
Lời giải:
a) Áp dụng định lí Thalès vào ∆ABC, ta có:
AMBM=ANCNAMBM=ANCN hay 6,5x=426,5x=42 .
Suy ra x=6,5 . 24=3,25x=6,5.24=3,25 (đvđd).
Vậy x = 3,25 (đvđd).
b) Ta có: PQ = PF + QF = 5 + 3,5 = 8,5 (đvđd).
Áp dụng định lí Thalès vào ∆PHQ, ta có:
PEPH=PFPQPEPH=PFPQ hay 4y=58,54y=58,5 .
Suy ra y=4 . 8,55=6,8y=4.8,55=6,8 (đvđd).
Vậy y = 6,8 (đvđd).
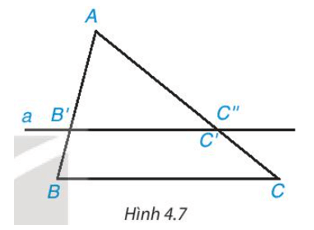
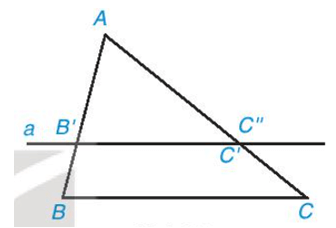
• So sánh các tỉ số AB'ABAB'AB và AC'ACAC'AC .
• Nhận xét gì về hai điểm C’, C’’ và hai đường thẳng B’C’, BC?
Lời giải:
• Ta có AB'AB=46=23AB'AB=46=23; AC'AC=69=23AC'AC=69=23 .
Do đó AB'AB=AC'ACAB'AB=AC'AC .
• Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên B’C’’ // BC.
Áp dụng định lí Thalès vào ∆ABC, ta có:
AB'AB=AC''ACAB'AB=AC''AC hay 46=AC''946=AC''9 .
Suy ra AC''=4 . 96=6AC''=4.96=6(cm).
Vậy AC’’ = 6 cm.
• Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.
Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao cho AC’’ = 6 cm.
Do đó, hai điểm C’, C’’ trùng nhau.
Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.
Vận dụng trang 80 Toán 8 Tập 1: Em hãy trả lời câu hỏi trong tình huống mở đầu.
Lời giải:
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
AEAB=CECDAEAB=CECD hay 400300=500CD400300=500CD.
Suy ra CD=300 . 500400=375CD=300.500400=375 (m).
Vậy khoảng cách giữa C và D bằng 375 m.
Bài tập
Lời giải:
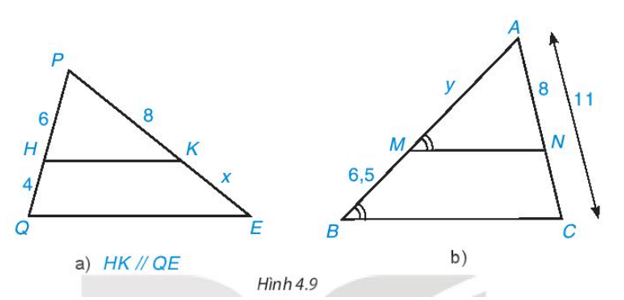
• Hình 4.9a)
Vì HK // QE nên áp dụng định lí Thalès, ta có:
PHQH=PKKEPHQH=PKKE hay 64=8x64=8x .
Suy ra x=8 . 46=163≈5,3x=8.46=163≈5,3 (đvđd).
• Hình 4.9b)
Vì ^AMN=^ABCˆAMN=ˆABC mà ^AMNˆAMN và ^ABCˆABC là hai góc đồng vị nên MN // BC.
Ta có AB = AM + BM = y + 6,5.
Áp dụng định lí Thalès, ta có: AMAB=ANACAMAB=ANAC hay yy+6,5=811yy+6,5=811 .
Suy ra 11y = 8(y + 6,5)
11y = 8y + 52
11y – 8y = 52
3y = 52
y=523≈17,3y=523≈17,3(đvđd)
Vậy x ≈ 5,3 (đvđd); y ≈ 17,3 (đvđd).
Lời giải:
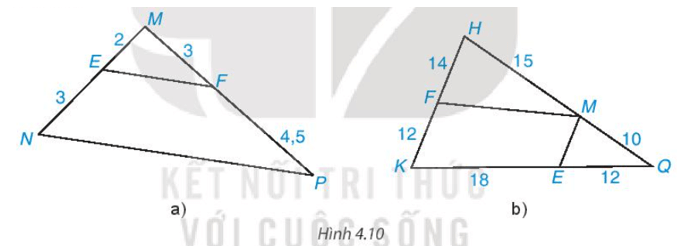
• Hình 4.10a)
Ta có EMEN=23; MFPF=34,5=23EMEN=23;MFPF=34,5=23 nên EMEN=MFPFEMEN=MFPF .
Vì EMEN=MFPFEMEN=MFPF , E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // MN.
• Hình 4.10b)
* Ta có: HFKF=1412=76; HMMQ=1510=32HFKF=1412=76;HMMQ=1510=32 .
Vì HFKF≠ HMMQHFKF≠HMMQ nên MF không song song với KQ.
* Ta có: MQMH=1015=23; EQEK=1218=23MQMH=1015=23;EQEK=1218=23 .
Vì MQMH=EQEKMQMH=EQEK ; F ∈ HK; M ∈ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.
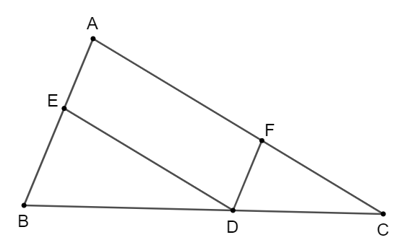
Chứng minh rằng: AEAB+AFAC=1AEAB+AFAC=1.
Lời giải:
Áp dụng định lí Thalès, ta có:
• Vì DE // AC nên AEAB=CDBCAEAB=CDBC;
• Vì DF // AC nên AFAC=BDBCAFAC=BDBC.
Khi đó, AEAB+AFAC=CDBC+BDBC=1AEAB+AFAC=CDBC+BDBC=1 (đpcm).
Lời giải:
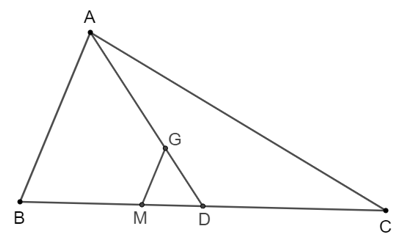
Lấy D là trung điểm của cạnh BC.
Khi đó, AD là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.
Ta có AGAD=23AGAD=23 hay AG=23ADAG=23AD.
Vì MG // AB, theo định lí Thalès, ta suy ra: AGAD=BMBD=23AGAD=BMBD=23.
Ta có BD = CD (vì D là trung điểm của cạnh BC) nên BMBC=BM2BD=22 . 3=13BMBC=BM2BD=22.3=13.
Do đó BM=13BCBM=13BC (đpcm).
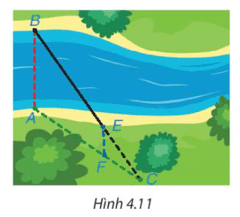
Lời giải:
Theo đề bài, ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF, áp dụng định lí Thalès, ta có:
ECBE=CFAFECBE=CFAF hay 30BE=204030BE=2040 .
Suy ra BE=30 . 4020=60BE=30.4020=60 (m).
Vậy khoảng cách giữa hai vị trí B và E bằng 60 m.
Lý thuyết Định lí Thalès trong tam giác
1. Khái niệm tỉ số của hai đoạn thẳng
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
2. Đoạn thẳng tỉ lệ
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức: ABCD=A′B′C′D′ hay ABA′B′=CDC′D′
3. Định lí Thalès
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.
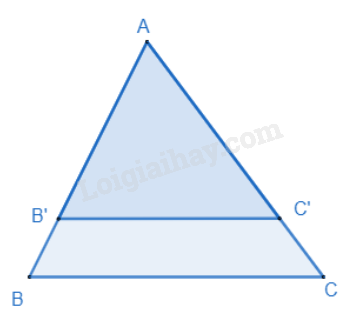
ΔABC,B'C'//BC(B'∈AB,C'∈AC)⇒AB'AB=AC'AC;AB'BB'=AC'CC';B'BAB=C'CAC
4. Định lí Thalès đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
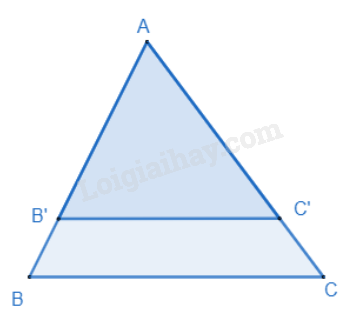
ΔABC,B'∈AB,C'∈AC,AB'AB=AC'AC⇒B'C'//BC
Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 15: Định lí Thalès trong tam giác
Bài 16: Đường trung bình của tam giác
Xem thêm các chương trình khác:
- Soạn văn 8 Kết nối tri thức (hay nhất)
- Văn mẫu lớp 8 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 8 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn lớp 8 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 8 - Kết nối tri thức
- Giải SBT Ngữ văn 8 – Kết nối tri thức
- Giải Vở thực hành Ngữ văn 8 Kết nối tri thức | VTH Ngữ văn 8 Tập 1, Tập 2
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Kết nối tri thức
- Soạn văn 8 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 8 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 8 – Global success
- Giải sbt Tiếng Anh 8 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 8 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 8 Global success
- Giải sgk Khoa học tự nhiên 8 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 8 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 8 – Kết nối tri thức
- Giải vth Khoa học tự nhiên 8 – Kết nối tri thức
- Giải sgk Lịch sử 8 – Kết nối tri thức
- Lý thuyết Lịch sử 8 - Kết nối tri thức
- Giải sbt Lịch sử 8 – Kết nối tri thức
- Giải sgk Địa lí 8 – Kết nối tri thức
- Lý thuyết Địa lí 8 - Kết nối tri thức
- Giải sbt Địa lí 8 – Kết nối tri thức
- Giải VTH Địa lí 8 Kết nối tri thức | Vở thực hành Địa lí 8
- Giải sgk Giáo dục công dân 8 – Kết nối tri thức
- Lý thuyết Giáo dục công dân 8 – Kết nối tri thức
- Giải sbt Giáo dục công dân 8 – Kết nối tri thức
- Giải sgk Công nghệ 8 – Kết nối tri thức
- Lý thuyết Công nghệ 8 - Kết nối tri thức
- Giải sbt Công nghệ 8 – Kết nối tri thức
- Giải sgk Tin học 8 – Kết nối tri thức
- Lý thuyết Tin học 8 - Kết nối tri thức
- Giải sbt Tin học 8 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 8 – Kết nối tri thức