Nội dung bài viết

    Xem thêm

    Toán 8 (Kết nối tri thức) Luyện tập chung (trang 108)

    Với giải bài tập Toán lớp 8 Luyện tập chung (trang 108) sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8.

    1 966 28/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Luyện tập chung (trang 108)

    Bài tập

    Giải Toán 8 trang 109 Tập 2

    Bài 9.32 trang 109 Toán 8 Tập 2: Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.

    a) Tính độ dài đoạn thẳng AH.

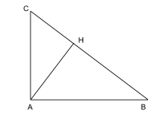
    b) Tính độ dài các đoạn thẳng AB và AC.

    Bài 9.32 trang 109 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    Lời giải:

    a) Có BC = BH + CH = 16 + 9 = 25 (cm).

    Xét tam giác ABC vuông tại A có: AB2 + AC2 = BC2 (định lý Pythagore).

    Xét tam giác AHC vuông tại H có: AC2 = AH2 + CH2 (định lý Pythagore).

    Suy ra AH2 = AC2 – CH2 (1).

    Xét tam giác AHB vuông tại H có: AH2 + BH2 = AB2 (định lý Pythagore).

    Suy ra AH2 = AB2 – BH2 (2).

    Xét (1) + (2), có:

    2AH2 = AC2 – CH2 + AB2 – BH2

    2AH2 = BC2 – CH2 – BH2 (vì AB2 + AC2 = BC2)

    2AH2 = 252 – 92 – 162

    2AH2 = 288

    AH2 = 144

    Suy ra AH = 12 (cm).

    b) Có AC2 = AH2 + CH2 = 122 + 92 = 225.

    Suy ra AC = 15 (cm).

    Có AB2 = AH2 + BH2 = 122 + 162 = 400.

    Suy ra AB = 20 (cm).

    Bài 9.33 trang 109 Toán 8 Tập 2: Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P.

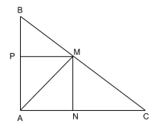
    a) Chứng minh rằng ΔBMP ∽ ΔMCN.

    b) Tính độ dài đoạn thẳng AM.

    Bài 9.33 trang 109 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    Lời giải:

    a) Vì BM = 4 cm; BC = 10 cm nên MC = 6 cm.

    Ta thấy 62 + 82 = 102 = 100 hay AB2 + AC2 = BC2 nên tam giác ABC vuông tại A.

    Lại có MN // AB (cùng vuông góc với AC) và MP // AC (cùng vuông góc với AB).

    Tam giác BMP vuông tại P và tam giác MCN vuông tại N có BMP^=MCN^ (MP // AC và hai góc ở vị trí đồng vị) nên ∆BMP ∽ ∆MCN.

    b) Tam giác BMP vuông tại P và tam giác BCA vuông tại A có góc B chung nên

    ∆BMP ∽ ∆BCA.

    Suy raBPAB=MPAC=BMBC=410=25

    Do đó, BP=2AB5=2⋅65=125 cm; MP=2CA5=2⋅85=165cm.

    Suy ra AP = AB – BP = 6 – 125=185 cm.

    Áp dụng định lí Pythagore cho tam giác vuông APM:

    AM2 = AP2 + MP2 = 58025⇒AM=2295 cm.

    Bài 9.34 trang 109 Toán 8 Tập 2: Trong Hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng:

    a) ΔAEH ∽ ΔAHB;

    b) ΔAFH ∽ ΔAHC;

    c) ΔAFE ∽ ΔABC.

    Bài 9.34 trang 109 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    Lời giải:

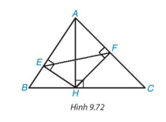
    a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có góc BAH chung.

    Suy ra ΔAEH ∽ ΔAHB.

    b) Xét hai tam giác AFH (vuông tại F) và tam giác AHC (vuông tại H) có góc CAH chung.

    Suy ra ΔAFH ∽ ΔAHC.

    c) Vì ΔAEH ∽ ΔAHB nên AEAH=AHAB⇒AE=AH2AB . (1)

    Vì ΔAFH ∽ ΔAHC nên AFAH=AHAC⇒AF=AH2AC . (2)

    Từ (1) và (2) suy ra AE . AB = AF. AC hay AFAB=AEAC .

    Tam giác AFE và tam giác ABC có BAC^chung; AFAB=AEAC .

    Do đó, ΔAFE ∽ ΔABC (c.g.c).

    Bài 9.35 trang 109 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ΔHBM∽ ΔHAN.

    Lời giải:

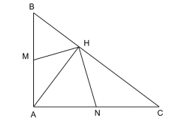
    Bài 9.35 trang 109 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    Ta có:HBA^=CBA^=90°−ACB^=HAC^(tam giác ABC vuông tại A và tam giác HAC vuông tại H).

    Xét hai tam giác HBA vuông tại H và tam giác HAC vuông tại H cóHBA^=HAC^ (chứng minh trên) nên ∆HBA ∽ ∆HAC.

    Suy ra HBHA=BAAC=2BM2AN=BMAN (Vì M, N là trung điểm của AB và AC).

    Xét tam giác HBM và tam giác HAN có

    BMAN=HBHA (chứng minh trên)

    HBA^=HAC^hay HBM^=HAN^

    Do đó ∆HBM ∽ ∆HAN (c.g.c).

    Bài 9.36 trang 109 Toán 8 Tập 2: Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m.

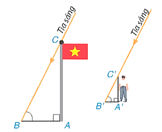
    a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?

    b) Vào buổi chiều khi bóng bạn An dài 3 m, hỏi bóng cột cờ dài bao nhiêu mét?

    Lời giải:

    Bài 9.36 trang 109 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    a) Ta có 60 cm = 0,6 m.

    Do tam giác vuông có hai cạnh góc vuông là cột cờ và bóng của cột cờ đồng dạng với tam giác vuông có hai cạnh góc vuông là An và bóng của An (vì góc tạo bởi cạnh huyền với mỗi chiếc bóng trong mỗi tam giác là góc tạo bởi tia nắng với chiếc bóng và chúng xem như bằng nhau do mặt trời ở rất xa). Vì vậy nếu gọi h là chiều cao cột cờ ta có:

    h1,4=30,6⇒h=3⋅1,40,6=7(m).

    Vậy cột cờ cao 7 m.

    b) Gọi k là chiều dài của bóng cột cờ vào lúc chiều, ta có:

    h1,4=k3⇒k=3h1,4=3⋅71,4=15(m).

    Vậy bóng cột cờ vào buổi chiều dài 15 m.

    Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

    Bài 37: Hình đồng dạng

    Bài tập cuối chương 9 trang 110

    Bài 38: Hình chóp tam giác đều

    Bài 39: Hình chóp tứ giác đều

    Luyện tập chung (trang 121)

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 966 28/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: