Nội dung bài viết

    Xem thêm

    Toán 8 Kết nối tri thức) Luyện tập chung (trang 91)

    Với giải bài tập Toán lớp 8 Luyện tập chung (trang 91) sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8.

    1 1,110 27/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Luyện tập chung (trang 91)

    Bài tập

    Giải Toán 8 trang 92 Tập 2

    Bài 9.11 trang 92 Toán 8 Tập 2: Cho ΔABC ∽ ΔDEF. Biết A^=60°, E^= 80°, hãy tính số đo các góc B^, C^,  D^,  F^ .

    Lời giải:

    Vì ΔABC ∽ ΔDEF. Suy ra A^=D^;  B^=E^;  C^=F^ .

    Mà A^=60°⇒D^=60°; E^=80° nên B^=80° .

    Có A^+B^+C^=180° , suy ra C^=F^=180°−60°−80°=40° .

    Bài 9.12 trang 92 Toán 8 Tập 2: Cho ΔABC ∽ ΔA'B'C'. Biết AB = 3 cm, A′B′ = 6 cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'.

    Lời giải:

    Vì ΔABC ∽ ΔA'B'C' nên 36=ABA'B'=ACA'C'=BCB'C'=AB+AC+BCA'B'+A'C'+B'C'.

    Suy ra A'B' + A'C' + B'C' = 2(AB + AC + BC) = 2 . 10 = 20 (cm).

    Vậy chu vi tam giác A'B'C' là 20 cm.

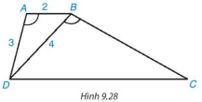
    Bài 9.13 trang 92 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có DAB^=DBC^.

    a) Chứng minh rằng ΔABD ∽ ΔBDC.

    b) Giả sử AB = 2 cm, AD = 3 cm, BD = 4 cm. Tính độ dài các cạnh BC và DC.

    Bài 9.13 trang 92 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    Lời giải:

    a) Vì AB // CD (giả thiết) nên ABD^=BDC^(2 góc ở vị trí so le trong).

    + Xét ΔABD và ΔBDC có: ABD^=BDC^,  DAB^=DBC^.

    Suy ra ΔABD ∽ ΔBDC (g.g).

    b) Ta có: ABBD=24=12.

    Vậy ΔABD ∽ ΔBDC với tỉ số đồng dạng 12 .

    Suy ra ADBC=BDDC=12 hay 3BC=4DC=12 .

    Suy ra BC = 2 . 3 = 6 cm; DC = 4 . 2 = 8 cm.

    Bài 9.14 trang 92 Toán 8 Tập 2: Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, DE = 4 cm, AB = 6 cm. Chứng minh rằng ΔAEF ∽ ΔECD và tính tỉ số đồng dạng.

    Bài 9.14 trang 92 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    Lời giải:

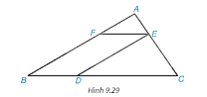
    - Có EF // BC. Suy ra AEF^=ACD^ (2 góc đồng vị). (1)

    - Có EF // BD (vì EF // BC) và DE // FB (vì ED // AB).

    Suy ra EFBD là hình bình hành. Suy ra EFB^=EDB^ .

    Mà EFB^+AFE^=180°;  EDB^+EDC^=180° (kề bù).

    Do đó, AFE^=EDC^ . (2)

    Từ (1) và (2) suy ra ΔAEF ∽ ΔECD (g.g).

    Vì EFBD là hình bình hành nên BF = ED = 4 cm.

    Mà AF + BF = AB nên AF = AB – BF = 6 – 4 = 2 cm.

    Khi đó, AFED=24=12 .

    Vậy ΔAEF ∽ ΔECD với tỉ số đồng dạng là 12 .

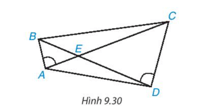
    Bài 9.15 trang 92 Toán 8 Tập 2: : Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng

    BAC^=CDB^

    .Chứng minh rằng ΔAED ∽ ΔBEC.

    Bài 9.15 trang 92 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    Lời giải:

    Xét ΔAEB và ΔDEC có:

    BAC^=CDB^ (giả thiết)

    AEB^=DEC^ (đối đỉnh)

    Suy ra ΔAEB ∽ ΔDEC (g.g).

    Suy ra AEDE=BECE⇒AEBE=DECE .

    Xét ΔAED và ΔBEC có:

    AED^=BEC^ (2 góc đối đỉnh)

    AEBE=DECE (chứng minh trên)

    Suy ra ΔAED ∽ ΔBEC (c.g.c).

    Bài 9.16 trang 92 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM = MD, 2BN = NC. Biết AB = 5 cm, CD = 6 cm, hãy tính độ dài đoạn thẳng MN.

    Lời giải:

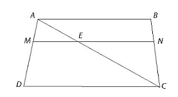
    Bài 9.16 trang 92 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

    Vẽ đường thẳng qua M song song với CD cắt AC tại E.

    Khi đó: AEEC=AMMD=12 (định lí Thalès).

    Do đó AEEC=BNNC=12 (2BN = NC), suy ra NE // AB (định lí Thalès đảo).

    Ta có:

    ME // CD

    NE // AB

    AB // CD

    Do đó ME // CD và NE // CD, suy ra M, N, E thẳng hàng.

    Mặt khác ∆AME ∽ ∆ADC (vì ME // CD).

    Nên MEDC=AMAD=13⇒ME=DC3=63=2(cm).

    Tương tự ∆CEN ∽ ∆CAB (vì NE //AB) nên ENAB=CNCB=23⇒EN=2AB3=103 (cm).

    Vậy MN = ME + EN = 163 (cm).

    Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

    Bài 34: Ba trường hợp đồng dạng của hai tam giác

    Bài 35: Định lí Pythagore và ứng dụng

    Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

    Bài 37: Hình đồng dạng

    Luyện tập chung (trang 108)

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,110 27/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: