Toán 8 Bài 22 (Kết nối tri thức): Tính chất cơ bản của phân thức đại số

Giải Toán 8 Bài 22: Tính chất cơ bản của phân thức đại số

Giải Toán 8 trang 8 Tập 2

Mở đầu trang 8 Toán 8 Tập 2: Liệu có phân thức nào đơn giản hơn nhưng bằng phân thức $\frac{x-y}{x^3-y^3}$ không nhỉ? Liệu có phân thức nào đơn giản hơn nhưng bằng phân thức $\frac{x-y}{x^3-y^3}$ không nhỉ?

Lời giải:

Sau bài học này ta trả lời được câu hỏi trên như sau:

Ta có $\frac{x-y}{x^3-y^3}=\frac{x-y}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\frac{1}{x^2+xy+y^2}$ .

Vậy có phân thức $\frac{1}{x^2+xy+y^2}$ thỏa mãn bài toán.

1. Tính chất cơ bản của phân thức

HĐ1 trang 8 Toán 8 Tập 2: Nếu nhân cả tử và mẫu của phân thức $\frac{x+y}{x-y}$với 2x ta được phân thức mới nào? Giải thích vì sao phân thức mới nhận được bằng phân thức đã cho.

Lời giải:

Nhân cả tử và mẫu của phân thức $\frac{x+y}{x-y}$ với 2x ta được: $\frac{2x(x+y)}{2x(x-y)}=\frac{2x^2+2xy}{2x^2-2xy}$ .

Ta có (x + y)(2x² – 2xy) = 2x³ – 2x²y + 2x²y – 2xy² = 2x³ – 2xy²;

(x – y)(2x² + 2xy) = 2x³ + 2x²y – 2x²y – 2xy² = 2x³ – 2xy².

Do đó, (x + y)(2x² – 2xy) = (x – y)(2x² + 2xy) nên $\frac{x+y}{x-y}=\frac{2x^2+2xy}{2x^2-2xy}$ .

HĐ2 trang 8 Toán 8 Tập 2: Tử và mẫu của phân thức $\frac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}$ có nhân tử chung là x – 1. Viết phân thức nhận được sau khi chia cả tử và mẫu của phân thức này cho nhân tử chung đó. So sánh phân thức mới nhận được và phân thức đã cho.

Lời giải:

Phân thức mới là: $\frac{x+1}{x^2+x+1}$ .

Ta thấy $\frac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{x+1}{x^2+x+1}$ .

Vì (x – 1)(x + 1)(x² + x + 1) = (x – 1)(x² + x + 1)(x + 1).

Giải Toán 8 trang 9 Tập 2

Luyện tập 1 trang 9 Toán 8 Tập 2: Khẳng định sau đây đúng hay sai? Vì sao?

$\frac{30x{y}^2(x-y)}{45xy{(x-y)}^2}=\frac{2y}{3(x-y)}$.

Lời giải:

Ta thấy tử và mẫu thức của phân thức $\frac{30x{y}^2(x-y)}{45xy{(x-y)}^2}$ có nhân tử chung là 15xy(x – y).

Chia tử cho nhân tử chung: 30xy²(x – y) : [15xy(x – y)] = 2y

Chia mẫu cho nhân tử chung: 45xy(x – y)² : [15xy(x – y)] = 3(x – y).

Vậy $\frac{30x{y}^2(x-y)}{45xy{(x-y)}^2}=\frac{2y}{3(x-y)}$ nên khẳng định đã cho là đúng.

Luyện tập 2 trang 9 Toán 8 Tập 2: Giải thích vì sao $\frac{-x}{1-x}=\frac{x}{x-1}$ .

Lời giải:

Nhân cả tử và mẫu của $\frac{-x}{1-x}$ với –1 ta được: $\frac{-x.(-1)}{(1-x)(-1)}=\frac{x}{x-1}$ .

Vậy $\frac{-x}{1-x}=\frac{x}{x-1}$ .

2. Vận dụng

a) Rút gọn phân thức

HĐ3 trang 9 Toán 8 Tập 2: Phân tích tử và mẫu của phân thức $\frac{2x^2+2x}{x^2-1}$ thành nhân tử và tìm các nhân tử chung của chúng.

Lời giải:

Ta có

2x² + 2x = 2x(x + 1)

x² – 1 = (x + 1)(x – 1)

Nhân tử chung của tử và mẫu là: x + 1.

HĐ4 trang 9 Toán 8 Tập 2: Chia cả tử và mẫu của phân thức $\frac{2x^2+2x}{x^2-1}$ cho các nhân tử chung, ta nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn.

Lời giải:

Ta có: $\frac{2x^2+2x}{x^2-1}$$=\frac{(2x^2+2x):(x+1)}{(x^2-1):(x+1)}=\frac{2x}{x-1}$ .

Giải Toán 8 trang 10 Tập 2

Luyện tập 3 trang 10 Toán 8 Tập 2: Em hãy trả lời câu hỏi trong tình huống mở đầu.

Lời giải:

Ta có: $\frac{x-y}{x^3-y^3}=\frac{(x-y).1}{(x-y)(x^2+xy+y^2)}=\frac{1}{x^2+xy+y^2}$ (Chia cả tử và mẫu cho nhân tử chung x – y).

Tranh luận trang 10 Toán 8 Tập 2: Tròn thực hiện rút gọn như hình bên. Hỏi bạn tròn làm đúng hay sai? Vì sao?

Lời giải:

Phân tích tử và mẫu thức thành nhân tử và rút gọn nhân tử chung ta có:

$\frac{x^2+2x}{3x^3+2x}=\frac{x(x+2)}{x(3x^2+2)}=\frac{x+2}{3x^2+2}$.

Vậy bạn Tròn đã làm sai.

Thử thách nhỏ trang 10 Toán 8 Tập 2: Tìm a sao cho hai phân thức sau bằng nhau:

$\frac{-a{x}^2-ax}{x^2-1}$ và $\frac{3x}{x-1}$ .

Lời giải:

$\frac{-a{x}^2-ax}{x^2-1}=\frac{-ax(x+1)}{(x-1)(x+1)}=\frac{-ax}{x-1}$.

Vậy để hai phân thức bằng nhau thì –ax = 3x suy ra a = –3.

b) Quy đồng mẫu thức nhiều phân thức

HĐ5 trang 10 Toán 8 Tập 2: Cho hai phân thức $\frac{1}{2x^2+2x}$ và $\frac{1}{3x^2-6x}$ .

Phân tích các mẫu thức của hai phân thức đã cho thành nhân tử.

Lời giải:

2x² + 2x = 2x(x + 1);

3x² – 6x = 3x(x – 2).

HĐ6 trang 10 Toán 8 Tập 2:

Cho hai phân thức $\frac{1}{2x^2+2x}$ và $\frac{1}{3x^2-6x}$ .

Chọn mẫu thức chung (MTC) của hai mẫu thức trên bằng cách lấy tích của các nhân tử được chọn như sau:

- Nhân tử bằng số của MTC là tích các nhân tử bằng số ở các mẫu thức của các phân thức đã cho (nếu các nhân tử bằng số ở các mẫu thức là những số nguyên dương thì nhân tử bằng số ở MTC là BCNN của chúng);

- Với mỗi lũy thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn lũy thừa với số mũ cao nhất.

Lời giải:

Mẫu thức chung của $\frac{1}{2x^2+2x}$ và $\frac{1}{3x^2-6x}$ là 6x(x + 1)(x – 2).

HĐ7 trang 10 Toán 8 Tập 2: Cho hai phân thức $\frac{1}{2x^2+2x}$ và $\frac{1}{3x^2-6x}$ .

Tìm nhân tử phụ của mỗi mẫu thức bằng cách lấy MTC chia cho mẫu thức đó.

Lời giải:

Ta có: Nhân tử phụ của $\frac{1}{2x^2+2x}$ là: 6x(x + 1)(x – 2) : 2x(x + 1) = 3(x – 2)

Nhân tử phụ của $\frac{1}{3x^2-6x}$ là: 6x(x + 1)(x – 2) : 3x(x – 2) = 2(x + 1).

HĐ8 trang 10 Toán 8 Tập 2: Cho hai phân thức $\frac{1}{2x^2+2x}$ và $\frac{1}{3x^2-6x}$ .

Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng, ta được các phân thức có mẫu thức là MTC đã chọn.

Lời giải:

$\frac{1}{2x^2+2x}$$=\frac{3(x-2)}{6x(x+1)(x-2)}$;

$\frac{1}{3x^2-6x}$$=\frac{2(x+1)}{6x(x+1)(x-2)}$.

Giải Toán 8 trang 11 Tập 2

Luyện tập 4 trang 11 Toán 8 Tập 2: Quy đồng mẫu thức hai phân thức $\frac{1}{3x^2-3}$ và $\frac{1}{x^3-1}$ .

Lời giải:

Ta có: 3x² – 3 = 3(x² – 1) = 3(x + 1)(x – 1)

x³ – 1 = (x – 1)(x² + x + 1)

MTC: 3(x + 1)(x – 1)(x² + x + 1).

Khi đó:

$\frac{1}{3x^2-3}=\frac{x^2+x+1}{3(x+1)(x-1)(x^2+x+1)}$;

$\frac{1}{x^3-1}=\frac{3(x+1)}{3(x+1)(x-1)(x^2+x+1)}$.

Tranh luận trang 11 Toán 8 Tập 2: Tròn nói hai phân thức $\frac{5}{x-1}$ và $\frac{x}{1-x}$ có MTC là x – 1. Vuông nói không đúng, MTC là (x – 1)(1 – x) chứ!

Theo em, bạn nào chọn MTC hợp lí hơn? Vì sao?

Lời giải:

Tròn hợp lí hơn, đơn giản hơn vì: $\frac{x}{1-x}=\frac{-x}{x-1}$ .

Bài tập

Bài 6.7 trang 11 Toán 8 Tập 2: Dùng tính chất cơ bản của phân thức, giải thích vì sao các kết luận sau đúng.

a) $\frac{{(x-2)}^3}{x^2-2x}=\frac{{(x-2)}^2}{x}$ ; b) $\frac{1-x}{-5x+1}=\frac{x-1}{5x-1}$ .

Lời giải:

a) $\frac{{(x-2)}^3}{x^2-2x}=\frac{{(x-2)}^2(x-2)}{x(x-2)}$$=\frac{{(x-2)}^2(x-2):(x-2)}{x(x-2):(x-2)}=\frac{{(x-2)}^2}{x}$ ;

b) $\frac{1-x}{-5x+1}=\frac{-(x-1)}{-(5x-1)}=\frac{x-1}{5x-1}$ .

Giải Toán 8 trang 12 Tập 2

Bài 6.8 trang 12 Toán 8 Tập 2: Tìm đa thức thích hợp cho dấu “?”.

$\frac{y-x}{4-x}=\frac{?}{x-4}$.

Lời giải:

Ta có: $\frac{y-x}{4-x}=\frac{-(x-y)}{-(x-4)}=\frac{x-y}{x-4}$ . Vậy đa thức cần tìm là x – y.

Bài 6.9 trang 12 Toán 8 Tập 2: Rút gọn các phân thức sau:

a) $\frac{5x+10}{25x^2+50}$ ;

b) $\frac{45x(3-x)}{15x{(x-3)}^3}$ ;

c) $\frac{{(x^2-1)}^2}{(x+1)(x^3+1)}$ .

Lời giải:

a) $\frac{5x+10}{25x^2+50}=\frac{5(x+2)}{25(x^2+2)}=\frac{x+2}{5(x^2+2)}$ ;

b) $\frac{45x(3-x)}{15x{(x-3)}^3}$$=\frac{-45x(x-3)}{15x{(x-3)}^3}=\frac{-3}{{(x-3)}^2}$ ;

c) $\frac{{(x^2-1)}^2}{(x+1)(x^3+1)}$$=\frac{(x^2-1)(x^2-1)}{(x+1)(x+1)(x^2-x+1)}$

$=\frac{(x-1)(x+1)(x-1)(x+1)}{(x+1)(x+1)(x^2-x+1)}=\frac{{(x-1)}^2}{x^2-x+1}$.

Bài 6.10 trang 12 Toán 8 Tập 2: Cho phân thức $P=\frac{x+1}{x^2-1}$ .

a) Rút gọn phân thức đã cho, kí hiệu Q là phân thức nhận được.

b) Tính giá trị của P và Q tại x = 11. So sánh hai kết quả đó.

Lời giải:

a) $P=\frac{x+1}{x^2-1}=\frac{x+1}{(x+1)(x-1)}=\frac{1}{x-1}$ . Vậy $Q=\frac{1}{x-1}$ .

b) $P\left(11\right)=\frac{11+1}{{11}^2-1}=\frac{12}{120}=\frac{1}{10}$ ; $Q\left(11\right)=\frac{1}{11-1}=\frac{1}{10}$ . Ta thấy hai kết quả cùng bằng $\frac{1}{10}$ .

Bài 6.11 trang 12 Toán 8 Tập 2: Tìm a sao cho hai phân thức sau bằng nhau:

$\frac{5x}{x+1}$ và $\frac{ax(x-1)}{(1-x)(x+1)}$ .

Lời giải:

Ta có $\frac{ax(x-1)}{(1-x)(x+1)}$$=\frac{-ax(1-x)}{(1-x)(x+1)}=\frac{-ax}{x+1}$ nên để hai phân thức $\frac{5x}{x+1}$ và $\frac{ax(x-1)}{(1-x)(x+1)}$ bằng nhau thì 5x = –ax hay a = –5.

Bài 6.12 trang 12 Toán 8 Tập 2: Quy đồng mẫu thức các phân thức sau:

a) $\frac{1}{x^3-8}$ và $\frac{3}{4-2x}$ ;

b) $\frac{x}{x^2-1}$ và $\frac{1}{x^2+2x+1}$ .

Lời giải:

a) MTC: 2(x – 2)(x² + 2x + 4)

$\frac{1}{x^3-8}=\frac{2}{2(x-2)(x^2+2x+4)}$;

$\frac{3}{4-2x}=\frac{-3}{2\left(x-2\right)}=\frac{-3\left(x^2+2x+4\right)}{2\left(x-2\right)\left(x^2+2x+4\right)}$.

b) MTC: (x – 1)(x + 1)²

$\frac{x}{x^2-1}$= $\frac{x}{(x+1)(x-1)}=\frac{x(x+1)}{(x-1){(x+1)}^2}$;

$\frac{1}{x^2+2x+1}=\frac{1}{{(x+1)}^2}=\frac{x-1}{(x-1){(x+1)}^2}$.

Bài 6.13 trang 12 Toán 8 Tập 2: Quy đồng mẫu thức các phân thức sau:

a) $\frac{1}{x+2};\frac{x+1}{x^2-4x+4}$ và $\frac{5}{2-x}$ ;

b) $\frac{1}{3x+3y};\frac{2x}{x^2-y^2}$ và $\frac{x^2-xy+y^2}{x^2-2xy+y^2}$ .

Lời giải:

a) MTC: (x + 2)(x – 2)²

$\frac{1}{x+2}=\frac{{(x-2)}^2}{(x+2){(x-2)}^2}$;

$\frac{x+1}{x^2-4x+4}=\frac{x+1}{{(x-2)}^2}=\frac{(x+1)(x+2)}{(x+2){(x-2)}^2}$;

$\frac{5}{2-x}=\frac{-5}{x-2}=\frac{-5(x+2)(x-2)}{(x+2){(x-2)}^2}$.

b) MTC: 3(x + y)(x – y)²

$\frac{1}{3x+3y}=\frac{1}{3\left(x+y\right)}=\frac{{(x-y)}^2}{3(x+y){(x-y)}^2}$;

$\frac{2x}{x^2-y^2}=\frac{2x}{(x+y)(x-y)}=\frac{2x.3(x-y)}{3(x+y){(x-y)}^2}$;

$\frac{x^2-xy+y^2}{x^2-2xy+y^2}=\frac{x^2-xy+y^2}{{(x-y)}^2}=\frac{3(x+y)(x^2-xy+y^2)}{3(x+y){(x-y)}^2}$.

Bài 6.14 trang 12 Toán 8 Tập 2: Cho hai phân thức $\frac{9x^2+3x+1}{27x^3-1}$ và $\frac{x^2-4x}{16-x^2}$

a) Rút gọn hai phân thức đã cho.

b) Quy đồng mẫu thức hai phân thức nhận được ở câu a.

Lời giải:

a) Rút gọn

$\frac{9x^2+3x+1}{27x^3-1}$ $=\frac{9x^2+3x+1}{{\left(3x\right)}^3-1^3}=\frac{9x^2+3x+1}{(3x-1)(9x^2+3x+1)}=\frac{1}{3x-1}$;

$\frac{x^2-4x}{16-x^2}$$=\frac{x(x-4)}{(4+x)(4-x)}=\frac{-x(4-x)}{(4+x)(4-x)}=\frac{-x}{x+4}$.

b) Quy đồng $\frac{1}{3x-1}$ và $\frac{-x}{x+4}$ .

$\frac{1}{3x-1}=\frac{x+4}{(3x-1)(x+4)}$;

$\frac{-x}{x+4}=\frac{-x(3x-1)}{(3x-1)(x+4)}$.

Lý thuyết Tính chất cơ bản của phân thức đại số

1. Tính chất cơ bản của phân thức

- Tính chất cơ bản của phân thức:

Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

$\frac{A}{B}=\frac{A.M}{B.M}$ (M là một đa thức khác đa thức không).

Nếu chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.

$\frac{A:N}{B:N}=\frac{A}{B}$ (N là nhân tử chung).

- Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.

$\frac{A}{B}=\frac{-A}{-B}$; $\frac{-A}{B}=\frac{A}{-B}=-\frac{A}{B}$.

Ví dụ: Để biến đổi phân thức $\frac{x-y}{y^2-x^2}$ thành $\frac{-1}{x+y}$, ta chia cả tử và mẫu của phân thức $\frac{x-y}{y^2-x^2}$ cho y – x, khi đó

$$\begin{gathered} \frac{x-y}{y^2-x^2} \\ =\frac{-(y-x)}{(y-x)(y+x)} \\ =\frac{-1}{x+y} \end{gathered}$$

2. Rút gọn phân thức

Rút gọn một phân thức là biến đổi phân thức đó thành một phân thức mới bằng nó nhưng đơn giản hơn.

Muốn rút gọn một phân thức đại số ta làm như sau:

- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung;

- Chia cả tử và mẫu cho nhân tử chung.

3. Quy đồng mẫu thức nhiều phân thức

Quy đồng mẫu thức nhiều phân thức là biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức và lần lượt bằng các phân thức đã cho.

Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:

- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;

- Tìm nhân tử phụ của mỗi mẫu thức bằng cách chia MTC của mẫu thức đó;

- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Ví dụ: Quy đồng mẫu thức hai phân thức $\frac{1}{x^2+x}$ và $\frac{1}{x^2-x}$

MTC là: $x\left(x+1\right)\left(x-1\right)$

Ta có:

$$\begin{gathered} \left[x\left(x+1\right)\left(x-1\right)\right]:\left[x(x+1)\right]=x-1; \\ \left[x\left(x+1\right)\left(x-1\right)\right]:\left[x(x-1)\right]=x+1 \end{gathered}$$

Khi đó:$$\begin{gathered} \frac{1}{x^2+x}=\frac{1}{x(x+1)}=\frac{x-1}{x(x+1)(x-1)}; \\ \frac{1}{x^2-x}=\frac{1}{x(x-1)}=\frac{x+1}{x(x-1)(x+1)} \end{gathered}$$

- Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.

$\frac{A}{B}=\frac{-A}{-B}$; $\frac{-A}{B}=\frac{A}{-B}=-\frac{A}{B}$.

Sơ đồ tư duy Tính chất cơ bản của phân thức đại số

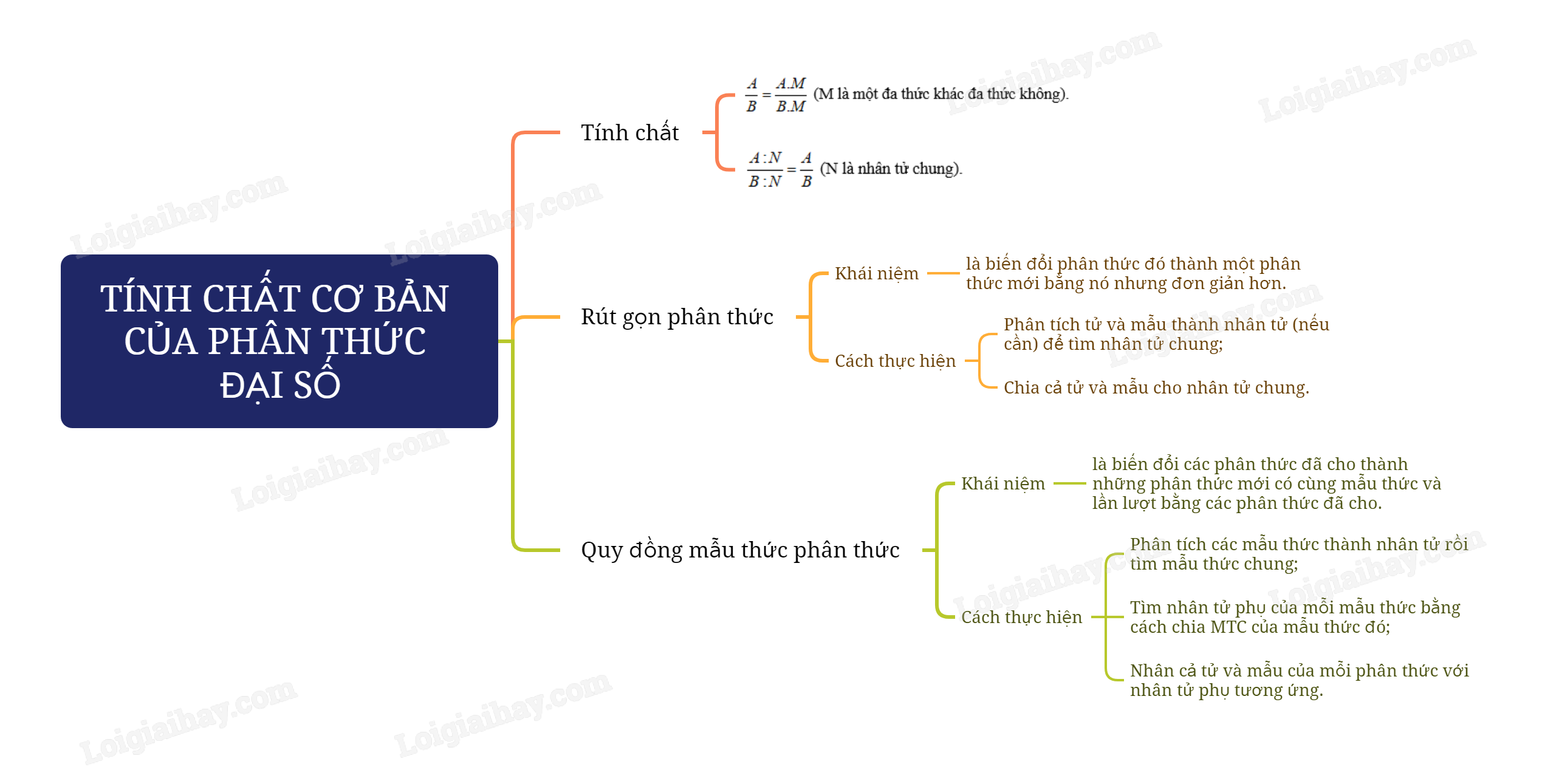
Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 21: Phân thức đại số

Luyện tập chung (trang 13, 14)

Bài 23: Phép cộng và phép trừ phân thức đại số

Bài 24: Phép nhân và phép chia phân thức đại số

Luyện tập chung (trang 23, 24)