Toán 8 Bài 31 (Kết nối tri thức): Cách tính xác suất của biến cố bằng tỉ số

Giải Toán 8 Bài 31: Cách tính xác suất của biến cố bằng tỉ số

Giải Toán 8 trang 64 Tập 2

Luyện tập 1 trang 64 Toán 8 Tập 2: Một túi đựng 20 viên kẹo giống hệt nhau nhưng khác loại, trong đó có 7 viên kẹo sữa, 4 viên kẹo chanh, 6 viên kẹo dừa và 3 viên kẹo bạc hà. Bạn Lan lấy ngẫu nhiên một viên kẹo từ túi. Tính xác suất để Lan lấy được:

a) Viên kẹo sữa;

b) Viên kẹo chanh.

Lời giải:

Có 20 kết quả có thể của hành động trên. Bạn Lan lấy ngẫu nhiên một viên kẹo từ túi nên các kết quả có thể là đồng khả năng.

a) Có 7 kết quả thuận lợi cho biến cố “Bạn Lan lấy được viên kẹo sữa”.

Vậy xác suất để Lan lấy được viên kẹo sữa là $\frac{7}{20}$.

b) Có 4 kết quả thuận lợi cho biến cố “Bạn Lan lấy được viên kẹo chanh”.

Vậy xác suất để Lan lấy được viên kẹo chanh là $\frac{4}{20}=\frac{1}{5}$

Giải Toán 8 trang 65 Tập 2

Luyện tập 2 trang 65 Toán 8 Tập 2: Trên giá sách của thư viện có 15 cuốn sách, trong đó có một số cuốn tiểu thuyết. Người thủ thư đặt thêm 5 cuốn tiểu thuyết thư viện mới mua vào giá sách. Bạn Nam đến mượn sách, chọn ngẫu nhiên một cuốn sách trên giá. Biết rằng xác suất để chọn được cuốn tiểu thuyết là $\frac{3}{4}$. Hỏi lúc đầu trên giá sách có bao nhiêu cuốn tiểu thuyết?

Lời giải:

Gọi số lượng cuốn tiểu thuyết ban đầu là x (cuốn).

Số lượng cuốn tiểu thuyết khi đặt thêm 5 cuốn tiểu thuyết mới mua là x + 5 (cuốn).

Theo đề bài ta có: $\frac{x+5}{15+5}=\frac{3}{4}$, tức là 4(x + 5) = 60 hay x + 5 = 15, suy x = 10.

Vậy ban đầu có 10 cuốn tiểu thuyết.

Tranh luận trang 65 Toán 8 Tập 2: Một túi đựng 17 viên bi cùng khối lượng và kích thước, chỉ khác màu, trong đó có 8 viên bi màu đỏ, 5 viên bi màu xanh và 4 viên bi màu vàng. Lấy ngẫu nhiên một viên bi từ trong túi. Tính xác suất của biến cố E: “Lấy được viên bi màu đỏ”.

Tròn: Có 17 viên bi, trong đó có 8 viên bi màu đỏ nên xác suất lấy được viên bi màu đỏ là $P\left(E\right)=\frac{8}{17}$.

Vuông: Các viên bi có ba màu đỏ, xanh, vàng nên xác suất lấy được viên bi màu đỏ là $P\left(E\right)=\frac{1}{3}$.

Vuông và Tròn ai nói đúng? Tại sao?

Lời giải:

Mặc dù chỉ có ba kết quả có thể là: bi màu đỏ, bi màu trắng và bi màu vàng nhưng ba kết quả có thể này là không đồng khả năng vì số bi màu đỏ, bi màu trắng và bi màu vàng là khác nhau. Do đó, Vuông nói sai.

Các viên bi có cùng khối lượng và kích thước nhưng ta có thể đánh số các viên bi từ 1 đến 17. Vì chọn ngẫu nhiên nên có 17 kết quả có thể là đồng khả năng.

Có 8 viên bi màu đỏ nên có 8 kết quả thuận lợi cho biến cố E.

Vậy $P\left(E\right)=\frac{8}{17}$.

Do đó, Tròn nói đúng.

Bài tập

Giải Toán 8 trang 66 Tập 2

Bài 8.4 trang 66 Toán 8 Tập 2: Một tấm bìa cứng hình tròn được chia thành 20 hình quạt như nhau, đánh số từ 1; 2;...; 20 và được gắn vào trục quay có mũi tên cố định ở tâm (H.8.2). Quay tấm bìa và quan sát xem mũi tên chỉ vào hình quạt nào khi tấm bìa dừng lại.

Tính xác suất để mũi tên:

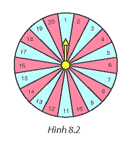
a) Chỉ vào hình quạt ghi số chia hết cho 4.

b) Chỉ vào hình quạt ghi số không phải là số nguyên tố.

Lời giải:

Có 20 kết quả có thể, đó là 1; 2;...; 20. Do 20 hình quạt như nhau nên 20 kết quả có thể này là đồng khả năng.

a) Từ 1 đến 20 có 4; 8; 12; 16; 20 chia hết cho 4, vậy có 5 hình quạt ghi số chia hết cho 4.

Gọi E là biến cố: “Mũi tên chỉ vào hình quạt ghi số chia hết cho 4”. Khi đó có 5 kết quả thuận lợi cho biến cố E.

Vậy xác suất để mũi tên chỉ vào hình quạt ghi số chia hết cho 4 là: $P\left(E\right)=\frac{5}{20}=\frac{1}{4}$

b) Có số 1; 4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20 không phải số nguyên tố, vậy có 12 hình quạt ghi số không phải là số nguyên tố.

Gọi F là biến cố: “Mũi tên chỉ vào hình quạt ghi số không phải là số nguyên tố”. Khi đó có 12 kết quả thuận lợi cho biến cố F.

Vậy xác suất để mũi tên chỉ vào hình quạt ghi số không phải là số nguyên tố là: $P\left(F\right)=\frac{12}{20}=\frac{3}{5}$.

Bài 8.5 trang 66 Toán 8 Tập 2: Một túi đựng các viên kẹo giống hệt nhau, chỉ khác màu, trong đó có 5 viên kẹo màu đen, 3 viên kẹo màu đỏ, 7 viên kẹo màu trắng. Lấy ngẫu nhiên một viên kẹo trong túi.

Tính xác suất của các biến cố sau:

a) E: "Lấy được viên kẹo màu đen";

b) F: "Lấy được viên kẹo màu đen hoặc màu đỏ";

c) G: "Lấy được viên kẹo màu trắng";

d) H: "Không lấy được viên kẹo màu đỏ".

Lời giải:

Trong túi có 5 + 3 + 7 = 15 (viên kẹo). Do đó, số kết quả có thể là 15.

Vì lấy ngẫu nhiên nên 15 kết quả có thể này là đồng khả năng.

a) Túi có 5 viên kẹo màu đen. Vậy có 5 kết quả thuận lợi cho E. Do đó $P\left(E\right)=\frac{5}{15}=\frac{1}{3}$.

b) Túi có 5 viên kẹo màu đen và 3 viên kẹo màu đỏ. Vậy có 5 + 3 = 8 kết quả thuận lợi cho F. Do đó $P\left(F\right)=\frac{8}{15}$.

c) Túi có 7 viên kẹo màu trắng. Vậy có 7 kết quả thuận lợi cho G. Do đó $P\left(G\right)=\frac{7}{15}$ .

d) Túi có 5 viên kẹo màu đen và 7 viên kẹo màu trắng, tức là có 5 + 7 = 12 viên kẹo không phải màu đỏ. Vậy có 12 kết quả thuận lợi cho H. Do đó $P\left(H\right)=\frac{12}{15}=\frac{4}{5}$

Bài 8.6 trang 66 Toán 8 Tập 2: Trong một chiếc hộp có 15 tấm thẻ giống nhau được đánh số 10; 11;...; 24. Rút ngẫu nhiên một tấm thẻ từ trong hộp. Tính xác suất của các biến cố sau:

a) A: "Rút được tấm thẻ ghi số lẻ";

b) B: "Rút được tấm thẻ ghi số nguyên tố".

Lời giải:

Có 15 kết quả có thể xảy ra. Do 15 tấm thẻ giống nhau nên 15 kết quả có thể này là đồng khả năng.

a) Có 11; 13; 15; 17; 19; 21; 23 là số lẻ nên có 7 kết quả thuận lợi cho biến cố A.

Do đó xác suất của biến cố A là $P\left(A\right)=\frac{7}{15}$

b) Có 11; 13; 17; 19; 23 là số nguyên tố nên có 5 kết quả thuận lợi cho biến cố B.

Do đó xác suất của biến cố B là $P\left(B\right)=\frac{5}{15}=\frac{1}{3}$

Bài 8.7 trang 66 Toán 8 Tập 2: Trò chơi vòng quay may mắn.

Một bánh xe hình tròn được chia thành 12 hình quạt như nhau, trong đó có 2 hình quạt ghi 100 điểm, 2 hình quạt ghi 200 điểm, 2 hình quạt ghi 300 điểm, 2 hình quạt ghi 400 điểm, 1 hình quạt ghi 500 điểm, 2 hình quạt ghi 1 000 điểm, 1 hình quạt ghi 2000 điểm (H.8.3). Ở mỗi lượt, người chơi quay bánh xe. Mũi tên cố định gắn trên vành bánh xe dừng ở hình quạt nào thì người chơi nhận được số điểm ghi trên hình quạt đó.

Bạn Lan chơi trò chơi này. Tính xác suất của các biến cố sau:

a) A: "Trong một lượt quay, Lan quay được 400 điểm";

b) B: "Trong một lượt quay, Lan được ít nhất 500 điểm".

Lời giải:

Mũi tên có thể dừng ở 1 trong 12 hình quạt như nhau nên 12 kết quả có thể này là đồng khả năng.

a) Có 2 hình quạt ghi 400 điểm nên có 2 kết quả thuận lợi cho biến cố A.

Do đó, xác suất của biến cố A là $P\left(A\right)=\frac{2}{12}=\frac{1}{6}$

b) Lan quay được ít nhất 500 điểm, tức là Lan có thể quay được 500 điểm hoặc 1 000 điểm hoặc 2 000 điểm.

Có 1 hình quạt ghi 500 điểm, 2 hình quạt ghi 1 000 điểm, 1 hình quạt ghi 2 000 điểm nên có 1 + 2 + 1 = 4 kết quả thuận lợi cho biến cố B.

Do đó, xác suất của biến cố B là $P\left(B\right)=\frac{4}{12}=\frac{1}{3}$.

Lý thuyết Cách tính xác suất của biến cố bằng tỉ số

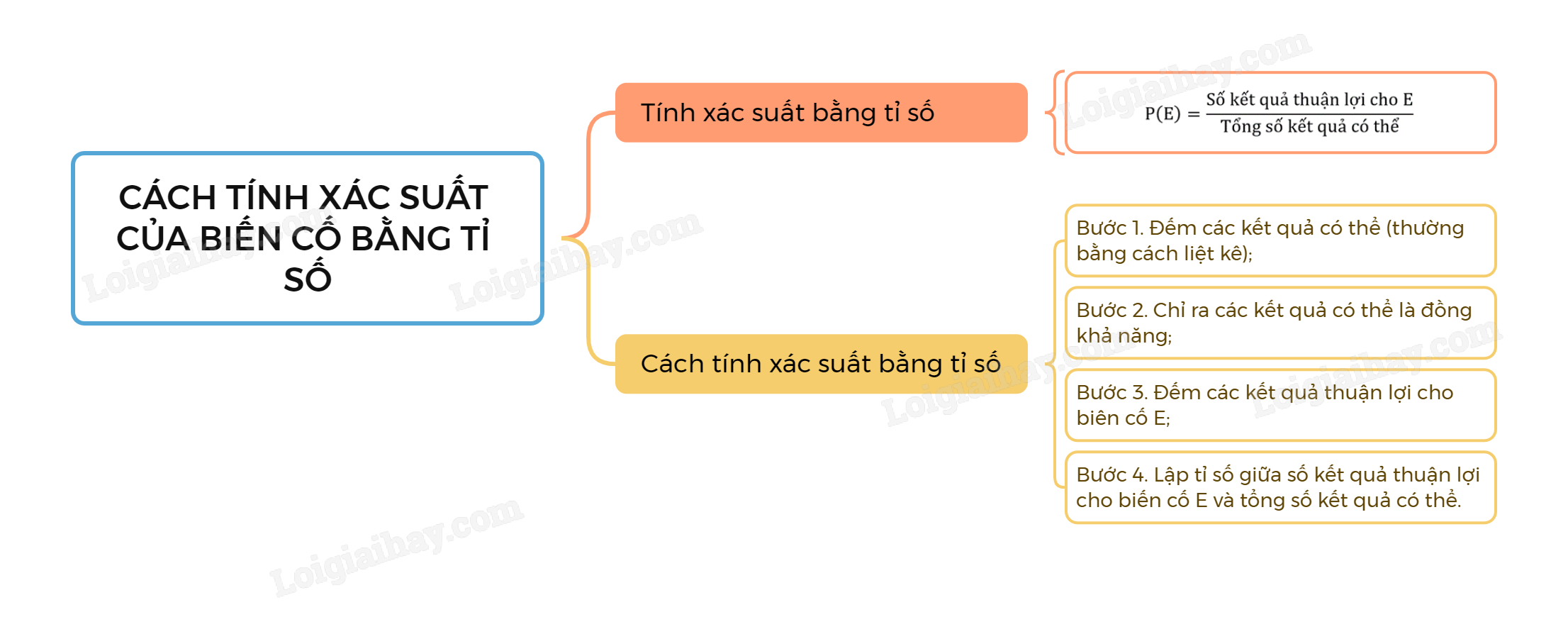
1. Tính xác suất bằng tỉ số

Giả thiết rằng các kết quả có thể của một hành động hay thực nghiệm là đồng khả năng. Khi đó, xác suất của biến cố E, kí hiệu là P(E), bằng tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.

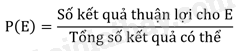
2. Cách tính xác suất bằng tỉ số

Việc tính xác suất của một biến cố E trong một hành động hay thực nghiệm đồng khả năng sẽ gồm các bước sau:

Bước 1. Đếm các kết quả có thể (thường bằng cách liệt kê);

Bước 2. Chỉ ra các kết quả có thể là đồng khả năng;

Bước 3. Đếm các kết quả thuận lợi cho biên cố E;

Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.

Ví dụ: Gieo một con xúc xắc.

Các kết quả có thể của hành động trên là 1, 2, 3, 4, 5, 6 chấm. Có 6 kết quả có thể.

Biến cố E: “Gieo được số chấm lẻ” xảy ra khi gieo được các số lẻ. Do đó các kết quả thuận lợi cho biến cố E là 1, 3, 5. Có 3 kết quả thuận lợi

Xác suất của biến cố E là: $P(E)=\frac{3}{6}=\frac{1}{2}$

Sơ đồ tư duy Cách tính xác suất của biến cố bằng tỉ số

Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 30: Kết quả có thể và kết quả thuận lợi

Bài 31: Cách tính xác suất của biến cố bằng tỉ số

Bài 32: Mối liên hệ giữa xác suất thực nghiệm với xác suất ứng dụng

Luyện tập chung (trang 74)

Bài tập cuối chương 8 trang 76