Toán 8 (Kết nối tri thức): Bài tập cuối chương 4 trang 89

Với giải bài tập Toán lớp 8 Bài tập cuối chương 4 trang 89 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8.

1 2,182 04/11/2023
Trang trước
Trang sau  

Giải Toán 8 Bài tập cuối chương 4 trang 89

Bài giảngToán 8 Bài tập cuối chương 4 trang 89

Trắc nghiệm

Giải Toán 8 trang 89

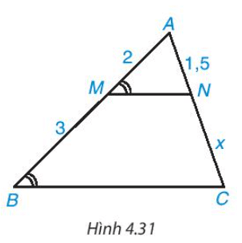
Bài 4.18 trang 89 Toán 8 Tập 1: Độ dài x trong Hình 4.31 bằng

Bài 4.18 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

A. 2,75

B. 2.

C. 2,25.

D. 3,75.

Lời giải:

Đáp án đúng là: C

Trong Hình 4.31 có ^AMN=^ABCˆAMN=ˆABC mà hai góc này ở vị trí đồng vị nên MN // BC.

Áp dụng định lí Thalès vào tam giác ABC, ta có:

AMBM=ANCNAMBM=ANCN hay 23=1,5x23=1,5x.

Suy ra x=1,5  .  32=2,25x=1,5.32=2,25.

Vậy x = 2,25.

Bài 4.19 trang 89 Toán 8 Tập 1: Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng

A. 3,5 cm.

B. 7 cm.

C. 10 cm.

D. 15 cm.

Lời giải:

Vì H, K lần lượt là trung điểm của AC, BC nên HK là đường trung bình của tam giác ABC suy ra HK=12ABHK=12AB.

Do đó AB = 2HK = 2 . 3,5 = 7 (cm).

Vậy AB = 7 cm.

Bài 4.20 trang 89 Toán 8 Tập 1: Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là

A. 8 cm.

B. 64 cm.

C. 30 cm.

D. 16 cm.

Lời giải:

Bài 4.20 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Đáp án đúng là: D

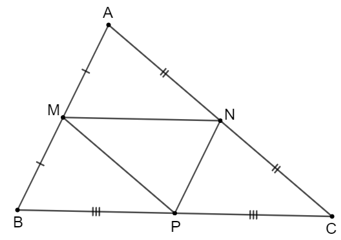
• Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN=12BCMN=12BC.

• Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP=12ABNP=12AB.

• Vì M, P lần lượt là trung điểm của các cạnh AB, BC nên NP là đường trung bình của tam giác ABC suy ra MP=12ACMP=12AC.

Chu vi tam giác ABC bằng: AB + BC + CA = 32 (cm).

Chu vi tam giác MNP bằng:

MN+NP+MP=12BC+12AB+12ACMN+NP+MP=12BC+12AB+12AC

=12(AB+BC+CA)=12  .  32=16=12(AB+BC+CA)=12.32=16 (cm)

Vậy chu vi tam giác MNP bằng 16 cm.

Bài 4.21 trang 89 Toán 8 Tập 1: Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng

A. 4 cm.

B. 5 cm.

C. 6 cm.

D. 7 cm.

Lời giải:

Bài 4.21 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Đáp án đúng là: A

Áp dụng định lí Thalès:

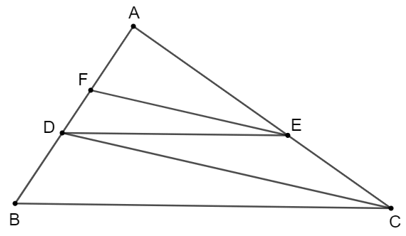
• Với DE // BC (E ∈ AC) ta có: ADAB=AEAC=912=23ADAB=AEAC=912=23;

• Với EF // CD (F ∈ AB) ta có: AFAD=AEAC=23AFAD=AEAC=23.

Suy ra AF=23AD=23  .  6  =4AF=23AD=23.6=4 (cm).

Vậy AF = 4 cm.

Bài 4.22 trang 89 Toán 8 Tập 1: Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là

A. 3 cm.

B. 6 cm.

C. 9 cm.

D. 12 cm.

Lời giải:

Bài 4.22 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Đáp án đúng là: C

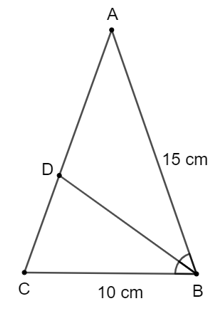
Vì tam giác ABC cân tại A nên AB = AC = 15 cm.

Theo đề bài, BD là tia phân giác của ^ABCˆABC, áp dụng tính chất đường phân giác vào tam giác ABC, ta có:

ABBC=ADCD=1510=32ABBC=ADCD=1510=32 suy ra AD3=CD2AD3=CD2.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

AD3=CD2=AD+CD3+2=AC5=155=3AD3=CD2=AD+CD3+2=AC5=155=3

Do đó AD = 3 . 3 = 9 (cm).

Vậy AD = 9 cm.

Tự luận

Bài 4.23 trang 89 Toán 8 Tập 1: Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.

Lời giải:

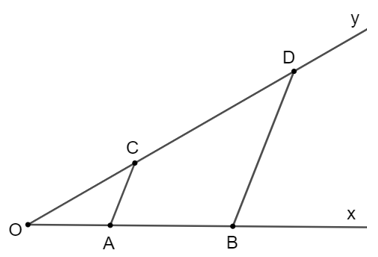
Bài 4.23 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D hay AC // BD.

Áp dụng định lí Thalès vào tam giác OBD, ta có:

OAOB=OCODOAOB=OCOD hay 25=3OD25=3OD .

Suy ra OD=5  .  32=7,5OD=5.32=7,5 (cm)

Ta có OD = OC + CD suy ra CD = OD – OC = 7,5 – 3 = 4,5 (cm).

Vậy CD = 4,5 cm.

Bài 4.24 trang 89 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.

a) Chứng minh rằng AE = DF.

b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.

Lời giải:

Bài 4.24 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

a) Theo đề bài, tam giác ABC vuông tại A nên ^BAC=90°ˆBAC=90° hay AB ⊥ AC.

Vì D, E lần lượt là trung điểm của AB, BC nên DE là đường trung bình của tam giác ABC suy ra DE // AC.

Mà AB ⊥ AC nên AB ⊥ DE hay ^ADE=90°ˆADE=90°.

Tương tự, ta chứng minh được: EF ⊥ AC hay ^AFE=90°ˆAFE=90°.

Ta có: ^BAC+^ADE+^AFE+^DEF=360°ˆBAC+ˆADE+ˆAFE+ˆDEF=360°

90°+90°+90°+^DEF=360°90°+90°+90°+ˆDEF=360°

270°+^DEF=360°270°+ˆDEF=360°

Suy ra ^DEF=360°−270°=90°ˆDEF=360°−270°=90°.

Tứ giác ADEF có ^BAC=90°;  ^ADE=90°;  ^AFE=90°;  ^DEF=90°ˆBAC=90°;ˆADE=90°;ˆAFE=90°;ˆDEF=90° .

Do đó tứ giác ADEF là hình chữ nhật.

Suy ra hai đường chéo AE và DF bằng nhau.

Vậy AE = DF (đpcm).

b) Vì D, F lần lượt là trung điểm của AB, AC nên DF là đường trung bình của tam giác ABC.

Suy ra DF // BC hay DF // BE.

Vì tứ giác ADEF là hình chữ nhật nên AD // EF hay BD // EF.

Tứ giác BDFE có DF // BE và BD // EF nên tứ giác BDFE là hình bình hành.

Hình bình hành BDFE có hai đường chéo BF và DE.

Mà I là trung điểm của DE nên I cũng là trung điểm của BF.

Do đó, ba điểm B, I, F thẳng hàng.

Bài 4.25 trang 89 Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.

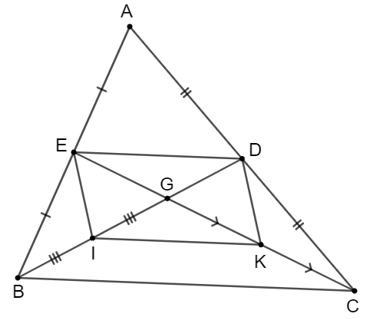
Lời giải:

Bài 4.25 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Vì BD và CE là đường trung tuyến nên E, D lần lượt là trung điểm của AB, AC.

Suy ra DE là đường trung bình của tam giác ABC.

Khi đó, DE // BC và DE=12BCDE=12BC (1)

Vì I, K lần lượt là trung điểm của GB, GC nên IK là đường trung bình của tam giác GBC suy ra IK // BC và IK=12BCIK=12BC (2)

Từ (1) và (2) suy ra DE // IK và DE=IK=12BCDE=IK=12BC.

Tứ giác EDKI có DE // IK và DE = IK nên tứ giác EDKI là hình bình hành (đpcm).

Bài 4.26 trang 89 Toán 8 Tập 1: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK (M thuộc AC), kẻ KN song song với CI (N thuộc AB). Chứng minh MN song song với BC.

Lời giải:

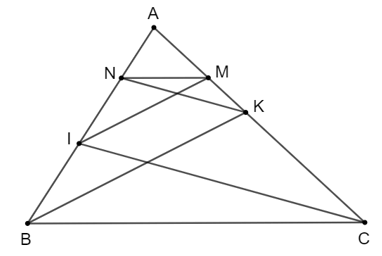
Bài 4.26 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Áp dụng định lí Thalès:

• Vì IM // BK nên AIAB=AMAKAIAB=AMAK suy ra AB.AM = AI.AK (1)

• Vì KN // IC nên ANAI=AKACANAI=AKAC suy ra AN.AC = AI.AK (2)

Từ (1) và (2) suy ra AB.AM = AN.AC = AI.AK

Do đó ANAB=AMACANAB=AMAC (theo tính chất tỉ lệ thức).

Suy ra MN // BC (theo định lí Thalès đảo).

Bài 4.27 trang 89 Toán 8 Tập 1: Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.32. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.

Lời giải:

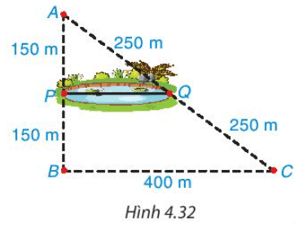
Bài 4.27 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Trong Hình 4.32 có AP = BP = 150 m; AQ = CQ = 250 m.

Suy ra PQ là đường trung bình của tam giác ABC.

Do đó PQ=12BC=12  .  400=200PQ=12BC=12.400=200 (m)

Vậy khoảng cách giữa hai điểm P và Q là 200 m.

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 15: Định lí Thalès trong tam giác

Bài 16: Đường trung bình của tam giác

Bài 17: Tính chất đường phân giác của tam giác

Luyện tập chung trang 88

Bài tập cuối chương 4

Tham khảo các loạt bài Toán 8 khác:

Bài viết cùng lớp mới nhất

Xem thêm
1 2,182 04/11/2023
Trang trước
Trang sau  

Xem thêm các chương trình khác: