Toán 8 Bài 9 (Kết nối tri thức): Phân tích đa thức thành nhân tử

Với giải bài tập Toán lớp 8 Bài 9: Phân tích đa thức thành nhân tử sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 9.

1 4,277 21/09/2024
Trang trước
Trang sau  

Giải Toán 8 Bài 9: Phân tích đa thức thành nhân tử

Bài giảng Toán 8 Bài 9: Phân tích đa thức thành nhân tử - Kết nối tri thức

1. Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung

Giải Toán 8 trang 42

HĐ 1 trang 42 Toán 8 Tập 1: Hãy viết đa thức x2−2xyx2−2xy thành tích của các đa thức, khác đa thức là số.

Phương pháp giải:

Áp dụng tính chất phân phối của phép nhân đối với phép cộng để đặt nhân tử chung.

Lời giải:

x2−2xy=x.x−2xy=x(x−2y)x2−2xy=x.x−2xy=x(x−2y)

Luyện tập 1 trang 42 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 6y3+2y6y3+2y

b) 4(x−y)−3x(x−y)4(x−y)−3x(x−y)

Phương pháp giải:

Áp dụng tính chất phân phối của phép nhân đối với phép cộng để đặt nhân tử chung.

Lời giải:

a) 6y3+2y=2y.(3y2+1)6y3+2y=2y.(3y2+1)

b) 4(x−y)−3x(x−y)=(x−y)(4−3x)4(x−y)−3x(x−y)=(x−y)(4−3x)

Vận dụng 1 trang 42 Toán 8 Tập 1: Giải bài toán mở đâu bằng cách phân tích 2x2+x2x2+x thành nhân tử.

Phương pháp giải:

Áp dụng tính chất phân phối của phép nhân đối với phép cộng để đặt nhân tử chung.

A.B=0⇔[A=0B=0

Lời giải:

2x2+x=0⇔x(2x+1)=0⇔[x=02x+1=0⇔[x=0x=−12

Vậy x=0;x=−12

2. Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức

Giải Toán 8 trang 43

Luyện tập 2 trang 43 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử

a) (x+1)2−y2

b) x3+3x2+3x+1

c) 8x3−12x2+6x−1

Lời giải

a) (x+1)2−y2=(x+1+y)(x+1−y)

b) x3+3x2+3x+1=(x+1)3

c) 8x3−12x2+6x−1=(2x)3−3.(2x)2.1+3.2x.1−13=(2x−1)3

3. Phân tích đa thức thành nhân tử bằng cách nhóm các hạng tử

Giải Toán 8 trang 44

Luyện tập 3 trang 44 Toán 8 Tập 1: Phân tích đa thức 2x2−4xy+2y−x thành nhân tử.

Phương pháp giải:

Sử dụng cách nhóm hạng tử

Lời giải:

2x2−4xy+2y−x=(2x2−4xy)+(2y−x)=2x(x−2y)−(x−2y)=(x−2y)(2x−1)

Vận dụng 2 trang 44 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức

A=x2+2y−2x−xy tại x=2022,y=2020

Phương pháp giải:

Phân tích đa thức thành nhân tử bằng cách nhóm hạng tử rồi thay các giá trị của x, y vào biểu thức.

Lời giải:

A=x2+2y−2x−xy=(x2+2y)−(2x+xy)=x(x+2)−x(2+y)=x[x+2−(2+y)]=x.(x−y)

Thay x=2022,y=2020 vào A ta được:

A=2022.(2022−2020)=2022.2=4044

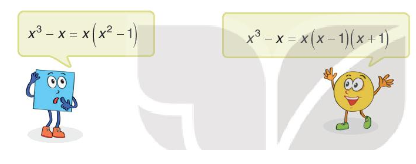
Tranh luận trang 44 Toán 8 Tập 1: Phân tích đa thức x3−x thành nhân tử.

(ảnh 2)

Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.

Phương pháp giải:

Kết hợp phương pháp đặt nhân tử chung và sử dụng hằng đẳng thức.

Lời giải:

x3−x=x(x2−1)=x(x−1)(x+1)

Bạn Tròn có kết quả đúng, bạn Vuông chưa phân tích triệt để.

Bài tập

Bài 2.22 trang 44 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a)x2+xy;b)6a2b−18ab;c)x3−4x;d)x4−8x.

Lời giải:

a)x2+xy=x.x+x.y=x(x+y);b)6a2b−18ab=6ab(a−3);c)x3−4x=x(x2−4)=x(x−2)(x+2);d)x4−8x=x(x3−8)=x(x−2)(x2+2x+4).

Bài 2.23 trang 44 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x2−9+xy+3y

b) x2y+x2+xy−1

Lời giải:

a)

x2−9+xy+3y=(x2−9)+(xy+3y)=(x−3)(x+3)+y(x+3)=(x+3)(x−3+y)

b)

x2y+x2+xy−1=(x2y+xy)+(x2−1)=xy(x+1)+(x+1)(x−1)=(x+1)(xy+x−1)

Bài 2.24 trang 44 Toán 8 Tập 1: Tìm x biết:

a) x2−4x=0

b) 2x3−2x=0

Lời giải:

a)

x2−4x=0⇔x(x−4)=0⇔[x=0x−4=0⇔[x=0x=4

Vậy x∈{0;4}

b)

2x3−2x=0⇔2x(x2−1)=0⇔2x(x−1)(x+1)=0⇔[x=0x−1=0x+1=0⇔[x=0x=1x=−1

Vậy x∈{0;1;−1}

Bài 2.25 trang 44 Toán 8 Tập 1: Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2)

(ảnh 1)

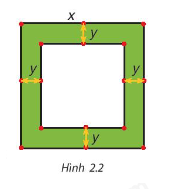
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.

b) Phân tích S thành nhân tử rồi tính A khi x=102 m, y=2 m.

Lời giải:

a) S=x2−(x−2y)2

b)

S=x2−(x−2y)2=(x−x+2y)(x+x−2y)=2y.(2x−2y)=2y.2(x−y)=4y(x−y)

Khi x=102 m, y=2 m thì S=4.2.(102−2)=800 (m2).

Lý thuyết Phân tích đa thức thành nhân tử

Phân tích đa thức thành nhân tử:

Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung:

Ví dụ: Phân tích đa thức x3+x thành nhân tử: x3+x=x.x2+x=x(x2+1)

Phân tích đa thức thành nhân tử bằng cách nhóm nhân tử:

Ví dụ: Phân tích đa thức xy+3z+xz+3y thành nhân tử:

xy+3z+xz+3y=(xy+xz)+(3z+3y)=x(y+z)+3(z+y)=(x+3)(y+z)

Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức như thế nào?

Ví dụ: Phân tích đa thức x2−8x+16 thành nhân tử: x2−8x+16=x2−2.x.4+42=(x−4)2

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 8: Tổng và hiệu hai lập phương

Luyện tập chung trang 41

Bài 9: Phân tích đa thức thành nhân tử

Luyện tập chung trang 45

Bài tập cuối chương 2

Tham khảo các loạt bài Toán 8 khác:

Bài viết cùng lớp mới nhất

Xem thêm
1 4,277 21/09/2024
Trang trước
Trang sau  

Xem thêm các chương trình khác: