Toán 8 Bài 1 (Kết nối tri thức): Đơn thức

Giải bài tập Toán 8 Bài 1: Đơn thức

Bài giảng Toán 8 Bài 1: Đơn thức - Kết nối tri thức

Mở đầu trang 5 Toán 8 Tập 1: Một nhóm thiện nguyện chuẩn bị y phần quà giúp đỡ những gia đình có hoàn cảnh khó khăn. Mỗi phần quà gồm x kg bao gạo và x gói mì ăn liền. Viết biểu thức giá trị bằng tiền (nghìn đồng) của toàn bộ số quà đó, biết 12 nghìn đồng/kg gạo; 4,5 nghìn đồng/gói mì ăn liền.

Hai bạn Tròn và Vuông lập luận như sau:

Bạn Vuông lập luận: Tổng số gạo trong y phần quà trị giá 12xy (nghìn đồng); tổng số gói mì ăn liền trong y phần quà trị giá 4,5xy (nghìn đồng). Vậy biểu thức cần tìm là 12xy + 4,5xy.

Bạn Tròn lập luận: Mỗi phần quà trị giá 12x + 4,5x = 16,5x (nghìn đồng). Do đó, y phần quà trị giá 16,5xy (nghìn đồng). Vậy biểu thức cần tìm là 16,5xy.

Theo em, bạn nào giải đúng?

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

Với giá tiền 12 nghìn đồng/kg gạo thì x bao gạo có giá 12x (nghìn đồng);

Với giá tiền 4,5 nghìn đồng/gói mì ăn liền thì x gói mì ăn liền có giá 4,5x (nghìn đồng).

Giá trị của mỗi phần quà là: 12x + 4,5x (nghìn đồng)

Giá trị của y phần quà là: (12x + 4,5x) . y = 12xy + 4,5xy = 16,5xy (nghìn đồng).

Vậy cách giải của hai bạn đều đúng.

1. Đơn thức và đơn thức thu gọn

Giải Toán 8 trang 6 Tập 1

HĐ1 trang 6 Toán 8 Tập 1: Biểu thức x² – 2x có phải là đơn thức một biến không? Vì sao? Hãy cho một vài ví dụ về đơn thức một biến.

Lời giải:

Biểu thức x² – 2x không phải là đơn thức một biến vì đơn thức một biến là biểu thức có chứa dạng tích của một số thực với một lũy thừa của biến.

Một số ví dụ về đơn thức một biến: $\frac{2}{5}{x}^{2}y;3xy{}_3;-5x^2{y}^2$.

HĐ2 trang 6 Toán 8 Tập 1: Xét các biểu thức đại số:

−5x²y; $x^3-\frac{1}{2}x$ ; 17z⁴; $-\frac{1}{5}{y}^{2}5$ ; −2x + 7y; xy4x²; x + 2y – z.

Hãy sắp xếp các biểu thức đó thành hai nhóm:

Nhóm 1: Những biểu thức có chứa phép cộng hoặc phép trừ.

Nhóm 2: Các biểu thức còn lại.

Nếu hiểu đơn thức (nhiều biến) tương tự đơn thức một biến thì theo em, nhóm nào trong hai nhóm trên bao gồm những đơn thức?

Lời giải:

Ta sắp xếp các biểu thức đó thành hai nhóm như sau:

Nhóm 1: Những biểu thức có chứa phép cộng hoặc phép trừ.

$x^3-\frac{1}{2}x$; −2x + 7y; x + 2y – z.

Nhóm 2: Các biểu thức còn lại.

−5x²y; 17z⁴; $-\frac{1}{5}{y}^{2}5$ ; xy4x².

Nếu hiểu đơn thức (nhiều biến) tương tự đơn thức một biến thì nhóm 2 gồm những đơn thức.

Luyện tập 1 trang 6 Toán 8 Tập 1: Trong các biểu thức sau đây, biểu thức nào là đơn thức?

3x³y; −4; (3 – x)x²y²; 12x⁵; $-\frac{5}{9}xyz$ ; $\frac{x^{2}y}{2}$; $\frac{3}{x}+y^2$ .

Lời giải:

Các biểu thức là đơn thức gồm: 3x³y; −4; 12x⁵;$-\frac{5}{9}xyz$ ; $\frac{x^{2}y}{2}$.

Tranh luận trang 6 Toán 8 Tập 1: Bạn Pi đặt câu hỏi: Biểu thức $\left(1+\sqrt{2}\right)x^{2}y$ có phải là đơn thức không?

Bạn Tròn trả lời: Mình nghĩ là đúng, đó là một đơn thức.

Bạn Vuông cho rằng: Mình nghĩ không phải, bởi trong đó có phép cộng.

Còn em nghĩ sao?

Lời giải:

Vì giá trị của $1+\sqrt{2}$ là một số thực nên biểu thức $\left(1+\sqrt{2}\right)x^{2}y$ là tích của số thực với các biến.

Do đó, biểu thức $\left(1+\sqrt{2}\right)x^{2}y$ là đơn thức.

Giải Toán 8 trang 8 Tập 1

Luyện tập 2 trang 8 Toán 8 Tập 1: Thu gọn và xác định bậc của đơn thức 4,5x²y(−2)xyz.

Lời giải:

Thu gọn đơn thức, ta được: 4,5x²y(−2)xyz = [4,5 . (−2)] (x² . x) (y . y) z = −9x³y²z.

Đơn thức −9x³y²z có bậc là 6 nên đơn thức đã cho có bậc là 6.

2. Đơn thức đồng dạng

HĐ3 trang 8 Toán 8 Tập 1: Cho đơn thức một biến M = 3x². Hãy viết ba đơn thức biến x, cùng bậc với M rồi so sánh phần biến của các đơn thức đó.

Lời giải:

Ta có thể viết được nhiều đơn thức biến x, cùng bậc với đơn thức 3x².

Chẳng hạn: $5x^2;\frac{3}{7}{x}^2;-4x^2$ .

So sánh phần biến của các đơn thức trên, ta được: $5>\frac{3}{7}>-4$ .

HĐ4 trang 8 Toán 8 Tập 1: Xét ba đơn thức A = 2x²y³, $B=-\frac{1}{2}{x}^2{y}^3$ và C = x³y². So sánh:

a) Bậc của ba đơn thức A, B và C;

b) Phần biến của ba đơn thức A, B và C.

Lời giải:

a) Ba đơn thức A, B và C đều có bậc là 5.

Do đó bậc của ba đơn thức A, B và C bằng nhau.

b) Hai đơn thức A và B đều có phần biến là x²y³; còn đơn thức C có phần biến là x³y².

Luyện tập 3 trang 8 Toán 8 Tập 1: Cho đơn thức:

$\frac{5}{3}{x}^{2}y;-x{y}^2;0,5x^4;-2x{y}^2;2,7x^4;3x{y}^2$.

Hãy sắp xếp các đơn thức đã cho thành từng nhóm, sao cho tất cả các đơn thức đồng dạng thì thuộc cùng một nhóm.

Lời giải:

Sắp xếp các đơn thức đã cho thành từng nhóm, ta được:

• Nhóm 1: −xy²; −2xy²; 3xy²;

• Nhóm 2: 0,5x⁴; 2,7x⁴;

• Nhóm 3: $\frac{5}{3}{x}^{2}y$ .

Tranh luận trang 8 Toán 8 Tập 1: Ta đã biết nếu hai đơn thức một biến có cùng biến và có cùng bậc thì đồng dạng với nhau. Hỏi điều đó còn đúng không đối với hai đơn thức hai biến (nhiều hơn một biến)?

Lời giải:

Hai đơn thức một biến có cùng biến và có cùng bậc thì đồng dạng với nhau. Điều này cũng đúng với hai đơn thức hai biến (nhiều hơn một biến).

HĐ5 trang 8 Toán 8 Tập 1: Quan sát các ví dụ sau:

2,5 . 3² . 5³ + 8,5 . 3² . 5³ = (2,5 + 8,5) . 3² . 5³ = 11 . 3² . 5³

Trong ví dụ này, ta đã vận dụng tính chất gì của phép nhân để thu gọn tổng ban đầu?

Lời giải:

Trong ví dụ này, ta đã vận dụng tính chất phân phối của phép nhân đối với phép cộng để thu gọn tổng ban đầu.

HĐ6 trang 8 Toán 8 Tập 1: Cho hai đơn thức đồng dạng M = 2,5x²y³ và P = 8,5x²y³. Tương tự HĐ5, hãy:

a) Thu gọn tổng M + P;

b) Thu gọn hiệu M – P.

Lời giải:

a) Ta có M + P = 2,5x²y³ + 8,5x²y³ = (2,5 + 8,5)x²y³ = 11x²y³;

b) Ta có M – P 2,5x²y³ – 8,5x²y³ = (2,5 – 8,5)x²y³ = –6x²y³.

Giải Toán 8 trang 9 Tập 1

Luyện tập 4 trang 9 Toán 8 Tập 1: Cho các đơn thức –x³y; 4x³y và –2x³y.

a) Tính tổng S của ba đơn thức đó.

b) Tính giá trị của tổng S tại x = 2; y = –3.

Lời giải:

a) Ta có S = –x³y + 4x³y + (–2x³y) = (–1 + 4 – 2)x³y = x³y.

b) Thay x = 2; y = –3 vào biểu thức S, ta được:

2³ . (–3) = 8 . (–3) = –24.

Vậy S = –24 tại x = 2; y = –3.

Vận dụng trang 9 Toán 8 Tập 1: Trở lại các lập luận của Tròn và Vuông trong tình huống mở đầu. Hãy trả lời và giải thích rõ tại sao.

Lời giải:

Với giá tiền 12 nghìn đồng/kg gạo thì x bao gạo có giá 12x (nghìn đồng);

Với giá tiền 4,5 nghìn đồng/gói mì ăn liền thì x gói mì ăn liền có giá 4,5x (nghìn đồng).

Giá trị của mỗi phần quà là: 12x + 4,5x (nghìn đồng)

Giá trị của y phần quà là: (12x + 4,5x) . y = 12xy + 4,5xy = 16,5xy (nghìn đồng).

Vậy cách giải của hai bạn đều đúng.

Bài tập

Bài 1.1 trang 9 Toán 8 Tập 1: Trong các biểu thức sau, biểu thức nào là đơn thức?

$-x;(1+x)y^2;(3+\sqrt{3})xy;0;\frac{1}{y}{x}^2;2\sqrt{xy}$.

Lời giải:

Các biểu thức là đơn thức gồm $-x;(3+\sqrt{3})xy;0$ .

Bài 1.2 trang 9 Toán 8 Tập 1: Cho các đơn thức:

$$\begin{gathered} A=4x(-2)x^{2}y;B=12,75xyz; \\ C=(1+2.4,5)x^{2}y\frac{1}{5}{y}^3;D=(2-\sqrt{5})x \end{gathered}$$

a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.

b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.

Lời giải:

a) Các đơn thức B và D là đơn thức đã thu gọn.

Ta thu gọn đơn thức A và C như sau:

A = 4x(−2)x²y = [4 . (−2)] (x . x²)y = −8x³y;

$C=(1+2.4,5)x^{2}y\frac{1}{5}{y}^3=\left(10.\frac{1}{5}\right)x^2\left(y^3.y\right)=2x^2{y}^4$.

b) Đơn thức A = −8x³y có hệ số là −8; phần biến là x³y và bậc là 4;

Đơn thức B = 12,75xyz có hệ số là 12,75; phần biến là xyz và bậc là 3;

Đơn thức C = 2x²y⁴ có hệ số là 2; phần biến là x²y⁴ và bậc là 6;

Đơn thức $D=(2-\sqrt{5})x$ có hệ số là $(2-\sqrt{5})$ ; phần biến là x và bậc là 1.

Giải Toán 8 trang 10 Tập 1

Bài 1.3 trang 10 Toán 8 Tập 1: Thu gọn rồi tính giá trị của mỗi đơn thức sau:

a) $A=(-2)x^{2}y\frac{1}{2}xy$ khi $x=-2;y=\frac{1}{2}$ .

b) B = xyz(−0,5)y²z khi x = 4; y = 0,5; z = 2.

Lời giải:

a) Ta có $A=(-2)x^{2}y\frac{1}{2}xy=\left((-2).\frac{1}{2}\right)\left(x^2.x\right)\left(y.y\right)=-x^3{y}^2$.

Thay $x=-2;y=\frac{1}{2}$ vào biểu thức A, ta được: $-{\left(-2\right)}^3.{\left(\frac{1}{2}\right)}^2=8.\frac{1}{4}=2$.

b) Ta có B = xyz(−0,5)y²z = (−0,5) x (y . y²)(z . z) = −0,5xy³z².

Thay x = ; y = 0,5; z = 2 vào biểu thức B, ta được:

(−0,5) . 4 . (0,5)³ . 2² = −2 . 0,125 . 4 = −0,25 . 4 = −1.

Bài 1.4 trang 10 Toán 8 Tập 1: Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau:

$3x^3{y}^2;-0,2x^2{y}^3;7x^3{y}^2;-4y;\frac{3}{4}{x}^2{y}^3;y\sqrt{2}$.

Lời giải:

Sắp xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng như sau:

Nhóm 1: 3x³y²; 7x³y²;

Nhóm 2: $-0,2x^2{y}^3;\frac{3}{4}{x}^2{y}^3$;

Nhóm 3: $-4y;y\sqrt{2}$ .

Bài 1.5 trang 10 Toán 8 Tập 1: Rút gọn rồi tính giá trị biểu thức:

$S=\frac{1}{2}{x}^2{y}^5-\frac{5}{2}{x}^2{y}^5$ khi x = −2 và y = 1.

Lời giải:

Ta có $S=\frac{1}{2}{x}^2{y}^5-\frac{5}{2}{x}^2{y}^5=\left(\frac{1}{2}-\frac{5}{2}\right)x^2{y}^5=-2x^2{y}^5$.

Thay x = −2 và y = 1 vào biểu thức S, ta được:

S = −2x²y⁵ = (−2) . (−2)² . 1⁵ = (−2) . 4 . 1 = −8.

Bài 1.6 trang 10 Toán 8 Tập 1: Tính tổng của bốn đơn thức:

$2x^2{y}^3;-\frac{3}{5}{x}^2{y}^3;-14x^2{y}^3;\frac{8}{5}{x}^2{y}^3$.

Lời giải:

Tổng của bốn đơn thức đã cho là:

$2x^2{y}^3+\left(-\frac{3}{5}{x}^2{y}^3\right)+\left(-14x^2{y}^3\right)+\frac{8}{5}{x}^2{y}^3$

$=\left(2-\frac{3}{5}-14+\frac{8}{5}\right)x^2{y}^3=-11x^2{y}^3$.

Bài 1.7 trang 10 Toán 8 Tập 1: Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến x và y biểu thị diện tích của mảnh đất đã cho bằng hai cách:

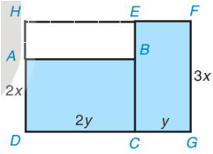
Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC.

Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA.

Lời giải:

Cách 1.Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC.

Diện tích hình chữ nhật ABCD là: 2x . 2y = 4xy (đvdt);

Diện tích hình chữ nhật EFGC là: 3x . y = 3xy (đvdt);

Diện tích mảnh đất tô màu xanh là: 4xy + 3xy = 7xy (đvdt).

Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA.

Diện tích hình chữ nhật HFGD là: 3x(2y + y) = 3x . 3y = 9xy (đvdt);

Diện tích hình chữ nhật HEBA là: (3x – 2x) . 2y = x . 2y = 2xy (đvdt);

Diện tích mảnh đất tô màu xanh là: 9xy – 2xy = 7xy (đvdt).

Lý thuyết Đơn thức

1. Đơn thức và đơn thức thu gọn

Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.

Số 0 được gọi là đơn thức không.

Ví dụ: $1;2xy;-\frac{3}{4}{x}^{2}y(-4x);...$ là các đơn thức.

Đơn thức thu gọn là đơn thức chỉ gồm một số, hoặc có dạng tích của một số với những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương.

Ví dụ:

$1;2xy;5x^2{y}^{4}z;...$ là các đơn thức thu gọn.

$3x^{2}yx;-\frac{3}{4}{x}^{2}y(-4x);...$ không phải là các đơn thức thu gọn.

Với các đơn chưa là đơn thức thu gọn, ta có thể thu gọn chúng bằng cách áp dụng các tính chất của phép nhân và phép nâng lên lũy thừa.

Ví dụ: $-\frac{3}{4}{x}^{2}y(-4x)=\left(-\frac{3}{4}\right).(-4).(x^2.x).y=3x^3.y$

Tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọi là bậc của đơn thức đó.

Chú ý: + Số thực khác 0 là đơn thức bậc không.

+ Số 0 được gọi là đơn thức không có bậc.

Ví dụ: $2xy$ có bậc là $1+1=2$

$5x^2{y}^{4}z$ có bậc là $2+4+1=7$

Với những đơn thức chưa thu gọn, ta nên thu gọn đơn thức trước, khi đó, bậc của đơn thức thu gọn chính là bậc của đơn thức ban đầu.

Ví dụ: $-\frac{3}{4}{x}^{2}y(-4x)$ có đơn thức thu gọn là $3x^3.y$, đơn thức này có bậc là $3+1=4$ nên đơn thức $-\frac{3}{4}{x}^{2}y(-4x)$ có bậc là 4.

Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.

Ví dụ: đơn thức $3x^3.y$ có hệ số là 3, phần biến là $x^3.y$.

2. Đơn thức đồng dạng

Hai đơn thức đồng dạng là hai đơn thức với hệ số khác 0 và có phần biến giống nhau.

- Cộng và trừ đơn thức đồng dạng: muốn cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài 2: Đa thức

Bài 3: Phép cộng và phép trừ đa thức

Luyện tập chung trang 17

Bài 4: Phép nhân đa thức

Bài 5: Phép chia đa thức