Toán 8 Bài 36 (Kết nối tri thức): Các trường hợp đồng dạng của hai tam giác vuông

Giải Toán 8 Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Giải Toán 8 trang 98 Tập 2

Mở đầu trang 98 Toán 8 Tập 2: Nam và Việt muốn đo chiều cao của cột cờ ở sân trường mà hai bạn không trèo lên được. Vào buổi chiều, Nam đo thấy bóng của cột cờ dài 6 m và bóng của Việt dài 70 cm. Nam hỏi Việt cao bao nhiêu, Việt trả lời là cao 1,4 m. Nam liền reo lên: "Tớ biết cột cờ cao bao nhiêu rồi đấy". Vậy cột cờ cao bao nhiêu và làm sao bạn Nam biết được.

Lời giải:

Qua bài này, các em sẽ có câu trả lời cho câu hỏi trên.

Tham khảo ở Luyện tập 1 trang 99.

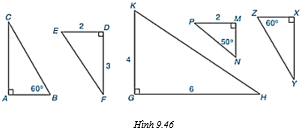
Câu hỏi trang 98 Toán 8 Tập 2: Hãy chỉ ra hai cặp tam giác vuông đồng dạng trong Hình 9.46.

Lời giải:

+ Hai tam giác ABC (vuông tại A) và tam giác XZY (vuông tại X) có:$\widehat{B}=\widehat{Z}=60°$

Do đó ∆ABC ∽ ∆XZY.

+ Hai tam giác DEF (vuông tại D) và tam giác GKH (vuông tại G) có:$\frac{DE}{GK}=\frac{DF}{GH}=\frac{1}{2}$

Do đó ∆DEF ∽ ∆GKH.

Giải Toán 8 trang 99 Tập 2

Luyện tập 1 trang 99 Toán 8 Tập 2: Trở lại tình huống mở đầu, ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC vuông tại đỉnh A, bạn Việt và bóng của mình cũng được xem là hai cạnh góc vuông của tam giác A'B'C' vuông tại đỉnh A' (H.9.48). Vì các tia sáng Mặt Trời tạo với hai cái bóng các góc bằng nhau nên $\widehat{B}=\widehat{B\text{'}}$ .

a) Hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không?

b) Bạn Nam đã tính chiều cao chiếc cột, tức là độ dài đoạn thẳng AC như thế nào và kết quả là bao nhiêu?

Lời giải:

a) Hai tam giác ABC vuông tại A và tam giác A'B'C' vuông tại A' có $\widehat{B}=\widehat{B\text{'}}$(giả thiết) nên ∆ABC ∽ ∆A'B'C'.

b) Ta có 70 cm = 0,7 m.

Vì ∆ABC ∽ ∆A'B'C' nên $\frac{A\text{'}B\text{'}}{AB}=\frac{A\text{'}C\text{'}}{AC}\Rightarrow \frac{\mathrm{0,7}}{6}=\frac{\mathrm{1,4}}{AC}$ .

Suy ra AC = 6 . 1,4 : 0,7 = 12 (m).

Giải Toán 8 trang 100 Tập 2

Thử thách nhỏ trang 100 Toán 8 Tập 2: Một người đo chiều cao của một cái cây bằng cách chôn một chiếc cọc xuống đất, cọc cao 2,4 m và cách vị trí gốc cây 19 m. Người đo đứng cách xa chiếc cọc 1 m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6 m (H.9.49).

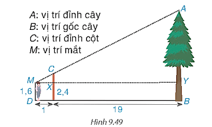
Lời giải:

Ta có CX = 2,4 – 1,6 = 0,8 (m).

MY = 1 + 19 = 20 (m).

Xét tam giác MXC và tam giác MYA có:

$\widehat{M}$chung

$\widehat{MXC}=\widehat{MYA}$

Do đó: ∆MXC ∽ ∆MYA (g.g).

Suy ra $\frac{CX}{AY}=\frac{MX}{MY}$ . Do đó, $AY=\frac{CX\cdot MY}{MX}=\frac{\mathrm{0,8}\cdot 20}{1}=16$ (m).

Vậy chiều cao của cây là AB = AY + YB = AY + MD = 16 + 1,6 = 17,6 m.

HĐ1 trang 100 Toán 8 Tập 2: Các tam giác vuông AHB và A'H'B' trong Hình 9.50 mô tả hai con dốc có chiều dài lần lượt là AB = 13 m, A′B′ = 6,5 m và độ cao lần lượt là BH = 5 m, B′H′ = 2,5 m. Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B'.

- Nhận xét về hai đại lượng $\frac{A\text{'}B\text{'}}{AB}và\frac{B\text{'}H\text{'}}{BH}$ .

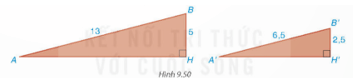
- Dùng định lí Pythagore để tính AH và A'H'.

- So sánh các đại lượng $\frac{A\text{'}H\text{'}}{AH}và\frac{B\text{'}H\text{'}}{BH}$.

- Hai tam giác vuông A'H'B' và AHB có đồng dạng không? Từ đó rút ra kết luận về độ dốc của hai con dốc.

Lời giải:

- Ta có: $\frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}H\text{'}}{BH}=\frac{1}{2}$ .

- Áp dụng định lí Pythagore cho tam giác vuông ABH ta có: AH² + BH² = AB², suy ra AH² = AB² – BH² = 13² – 5² = 144.

Suy ra AH = 12 (m).

- Tương tự ta có: A'H'² = A'B'² – B'H'² = (6,5)² – (2,5)² = 36. Suy ra A'H' = 6 (m).

- Vậy $\frac{A\text{'}H\text{'}}{AH}=\frac{1}{2}=\frac{B\text{'}H\text{'}}{BH}$ .

Do đó hai tam giác vuông A'H'B' và AHB đồng dạng, suy ra $\widehat{A}=\widehat{A\text{'}}$ .

Vậy hai con dốc có độ dốc như nhau.

Giải Toán 8 trang 102 Tập 2

Luyện tập 2 trang 102 Toán 8 Tập 2: Một ngôi nhà với hai mái lệch AB, CD được thiết kế như Hình 9.54 sao cho CD = 6 m, AB = 4 m, HA = 2 m, AC = 1 m. Chứng tỏ rằng $\widehat{ABD}=\widehat{CDB}$ .

Lời giải:

Ta có $\frac{AB}{CD}=\frac{4}{6}=\frac{2}{3}$; CH = AC + AH = 1 + 2 = 3 nên $\frac{AH}{CH}=\frac{2}{3}$ .

Xét hai tam giác ABH vuông tại H và tam giác CDH vuông tại H có:

$\frac{AB}{CD}=\frac{AH}{CH}=\frac{2}{3}$.

Do đó ∆ABH ∽ ∆CDH.

Suy ra $\widehat{ABD}=\widehat{ABH}=\widehat{CDH}=\widehat{CDB}$ . Vậy $\widehat{ABD}=\widehat{CDB}$ .

Vận dụng trang 102 Toán 8 Tập 2: Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72 cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1 m thì có thể đặt chiếc tivi mới vào đó không?

Lời giải:

- Gọi chiều ngang của chiếc ti vi mới là x (m).

Xét hai tam giác vuông lần lượt có các cạnh góc vuông là hai cạnh (nằm ngang và thẳng đứng) của màn hình hai chiếc tivi 32 inch và 55 inch. Đường chéo của chúng có độ dài lần lượt là 32 inch và 55 inch. Hai tam giác vuông này đồng dạng với nhau vì có hai cặp cạnh góc vuông tỉ lệ. Do đó $\frac{x}{72}=\frac{55}{32}\Rightarrow x=\frac{55\cdot 72}{32}=\mathrm{123,75}$ cm = 1,2375 m > 1 m.

Vậy không thể đặt vừa chiếc ti vi 55 inch vào khoảng trống hình vuông cạnh 1 m.

Bài tập

Bài 9.23 trang 102 Toán 8 Tập 2: Điều kiện nào dưới đây chứng tỏ rằng hai tam giác vuông đồng dạng?

a) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia.

b) Cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác kia.

c) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia.

d) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia.

Lời giải:

Các giả thiết a), b) và d) suy ra hai tam giác vuông đồng dạng, giả thiết c) không suy ra hai tam giác vuông đồng dạng.

+ Giả thiết a) suy ra hai tam giác vuông đồng dạng theo trường hợp góc – góc.

+ Giả thiết b) suy ra hai tam giác vuông đồng dạng theo trường hợp cạnh huyền – cạnh góc vuông.

+ Giả thiết d) suy ra hai tam giác vuông đồng dạng theo trường hợp cạnh – góc – cạnh.

Giải Toán 8 trang 103 Tập 2

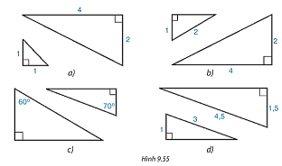
Bài 9.24 trang 103 Toán 8 Tập 2: Cặp tam giác vuông nào đồng dạng với nhau trong Hình 9.55?

Lời giải:

+ Vì $\frac{1}{1}\ne \frac{2}{4}$ nên cặp tam giác vuông ở hình a) không đồng dạng.

+ Độ dài cạnh góc vuông còn lại ở tam giác vuông có một cạnh bằng 1 ở hình b) là $\sqrt{2^2-1^1}=\sqrt{3}$ , khi đó $\frac{\sqrt{3}}{1}\ne \frac{4}{2}$ nên cặp tam giác vuông ở hình b) không đồng dạng.

+ Tính số đo hai góc nhọn chưa biết trong hai hình vuông ở hình c) ta được kết quả là 30° và 20° nên cặp tam giác vuông ở hình c) không đồng dạng.

+ Cặp tam giác vuông ở hình d) đồng dạng với nhau. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia $\left(\frac{1}{\mathrm{1,5}}=\frac{3}{\mathrm{4,5}}=\frac{2}{3}\right)$ .

Bài 9.25 trang 103 Toán 8 Tập 2: Cho góc nhọn xOy, các điểm A, N nằm trên tia Ox, các điểm B, M nằm trên tia Oy sao cho AM, BN lần lượt vuông góc với Oy, Ox. Chứng minh rằng ∆OAM ∽∆OBN.

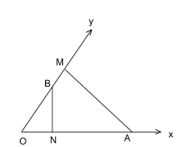
Lời giải:

Xét hai tam giác vuông OBN (vuông tại N) và tam giác OAM (vuông tại M) có:

Góc nhọn $\widehat{O}$ chung.

Suy ra ΔOAM ∽ ΔOBN.

Bài 9.26 trang 103 Toán 8 Tập 2: Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC = 3AB, B′D′ = 3A′B′.

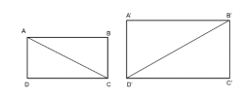
a) Chứng minh rằng ΔABC ∽ ΔA'B'C'.

b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là 2 m² thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu?

Lời giải:

a) Ta có AC = 3AB. Suy ra $\frac{AB}{AC}=\frac{1}{3}$ .

- Có B′D′ = 3A′B′. Suy ra $\frac{A\text{'}B\text{'}}{B\text{'}D\text{'}}=\frac{1}{3}$ .

Do đó, $\frac{AB}{AC}=\frac{A\text{'}B\text{'}}{B\text{'}D\text{'}}$, suy ra $\frac{AB}{A\text{'}B\text{'}}=\frac{AC}{B\text{'}D\text{'}}$.

Mà A'B'C'D' là hình chữ nhật nên A'C' = B'D', do đó $\frac{AB}{A\text{'}B\text{'}}=\frac{AC}{A\text{'}C\text{'}}$ .

Xét tam giác vuông ABC (vuông tại B) và tam giác vuông A'B'C' (vuông tại B') có

$\frac{AB}{A\text{'}B\text{'}}=\frac{AC}{A\text{'}C\text{'}}$.

Suy ra ΔABC ∽ ΔA′B′C′ (cạnh huyền – cạnh góc vuông).

b) Vì A′B′ = 2AB. Suy ra $\frac{AB}{A\text{'}B\text{'}}=\frac{1}{2}$.

Mà ΔABC ∽ ΔA'B'C'. Suy ra $\frac{AC}{A\text{'}C\text{'}}=\frac{BC}{B\text{'}C\text{'}}=\frac{AB}{A\text{'}B\text{'}}=\frac{1}{2}$.

+ Ta có diện tích hình chữ nhật ABCD là: AB ∙ BC

+ Diện tích hình chữ nhật A'B'C'D' là: A′B′ ∙ B′C′.

Xét tỉ lệ diện tích hai hình chữ nhật ABCD và A'B'C'D', có

$\frac{AB\cdot BC}{A\text{'}B\text{'}\cdot BC}=\frac{AB}{A\text{'}B\text{'}}\cdot \frac{BC}{B\text{'}C\text{'}}=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$.

Suy ra A′B′ ∙ B′C′ = 4AB ∙ BC = 4 ∙ 2 = 8 m².

Vậy diện tích hình chữ nhật A'B'C'D' là 8 m².

Bài 9.27 trang 103 Toán 8 Tập 2: Cho ΔA'B'C' ∽ ΔABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC.

Chứng minh rằng:

a)$\frac{A\text{'}H\text{'}}{AH}=k$.

b) Diện tích tam giác A'B'C' bằng k² lần diện tích tam giác ABC.

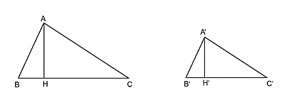
Lời giải:

a) Vì ΔA'B'C' ∽ ∆ABC theo tỉ số k nên $\widehat{B}=\widehat{B\text{'}};\frac{A\text{'}B\text{'}}{AB}=\frac{A\text{'}C\text{'}}{AC}=\frac{B\text{'}C\text{'}}{BC}=k$ .

Xét tam giác A'H'B' vuông tại H' và tam giác AHB vuông tại H có: $\widehat{B}=\widehat{B\text{'}}$ .

Do đó ∆A'H'B' ∽ ∆AHB.

Suy ra $\frac{A\text{'}H\text{'}}{AH}=\frac{A\text{'}B\text{'}}{AB}=k$.

b) Diện tích tam giác ABC là $\frac{1}{2}\cdot AH\cdot BC$

Diện tích tam giác A'B'C' là $\frac{1}{2}\cdot A\text{'}H\text{'}\cdot B\text{'}C\text{'}$

Xét tỉ lệ diện tích giữa hai tam giác A'B'C' và tam giác ABC:

$\frac{\frac{1}{2}A\text{'}H\text{'}\cdot B\text{'}C\text{'}}{\frac{1}{2}AH\cdot BC}=\frac{A\text{'}H\text{'}}{AH}\cdot \frac{B\text{'}C\text{'}}{BC}=k\cdot k=k^2$ Suy ra $\frac{1}{2}A\text{'}H\text{'}\cdot B\text{'}C\text{'}=k^2\cdot \frac{1}{2}AH\cdot BC$ .

Vậy diện tích tam giác A'B'C' bằng k² lần diện tích tam giác ABC.

Bài 9.28 trang 103 Toán 8 Tập 2: Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM = 2 m, AM vuông góc với AB và đo được số đo góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A'M'B' vuông tại A' có A'M' = 1 cm, $\widehat{A\text{'}M\text{'}B\text{'}}=\widehat{AMB}$ và đo được A'B' = 5 cm (H.9.56). Hỏi khoảng cách từ A đến B là bao nhiêu mét?

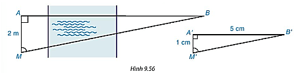
Lời giải:

Ta có A'M' = 1 cm = 0,01 m; A'B' = 5 cm = 0,05 m.

Xét ΔA′M′B′ (vuông tại A') và ΔAMB (vuông tại A) có $\widehat{A\text{'}M\text{'}B\text{'}}=\widehat{AMB}$ (giả thiết).

Do đó, ΔA′M′B′ ∽ ΔAMB.

Suy ra $\frac{A\text{'}M\text{'}}{AM}=\frac{A\text{'}B\text{'}}{AB}$ hay $\frac{\mathrm{0,01}}{2}=\frac{\mathrm{0,05}}{AB}$ . Suy ra AB $=\frac{\mathrm{0,05}\cdot 2}{\mathrm{0,01}}$ = 10 (m).

Vậy khoảng cách từ A đến B là 10 m.

Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông

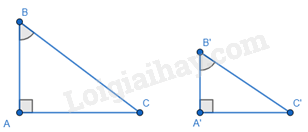
1. Trường hợp góc – góc:

Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đồng dạng với nhau.

$\begin{array}{l}\mathrm{\Delta }ABC,\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }:\\ \{\begin{array}{l}\hat{A}=\widehat{A^{\prime }}={90}^0\\ \hat{B}=\widehat{B^{\prime }}\end{array}\Rightarrow \mathrm{\Delta }ABC\backsim \mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\end{array}$

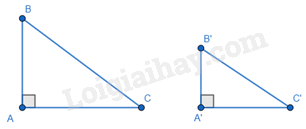
2. Trường hợp hai cạnh góc vuông:

Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

$\begin{array}{l}\mathrm{\Delta }ABC,\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }:\\ \{\begin{array}{l}\hat{A}=\widehat{A^{\prime }}={90}^o\\ \frac{AB}{A^{\prime }{B}^{\prime }}=\frac{AC}{A^{\prime }{C}^{\prime }}\end{array}\Rightarrow \mathrm{\Delta }ABC\backsim \mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\end{array}$

3. Trường hợp cạnh huyền – cạnh góc vuông:

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

$\begin{array}{l}\mathrm{\Delta }ABC,\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }:\\ \{\begin{array}{l}\hat{A}=\widehat{A^{\prime }}={90}^o\\ \frac{AB}{A^{\prime }{B}^{\prime }}=\frac{BC}{B^{\prime }{C}^{\prime }}\end{array}\Rightarrow \mathrm{\Delta }ABC\backsim \mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\end{array}$

Nhận xét: Nếu $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\backsim \mathrm{\Delta }ABC$ theo tỉ số k và AH, A’H’ lần lượt là các đường cao của $\mathrm{\Delta }ABC$ và $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }$ thì $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{H}^{\prime }\backsim \mathrm{\Delta }ABH$ (do $\hat{B}=\widehat{B^{\prime }}$) theo tỉ số k và $\frac{A^{\prime }{H}^{\prime }}{AH}=k$.

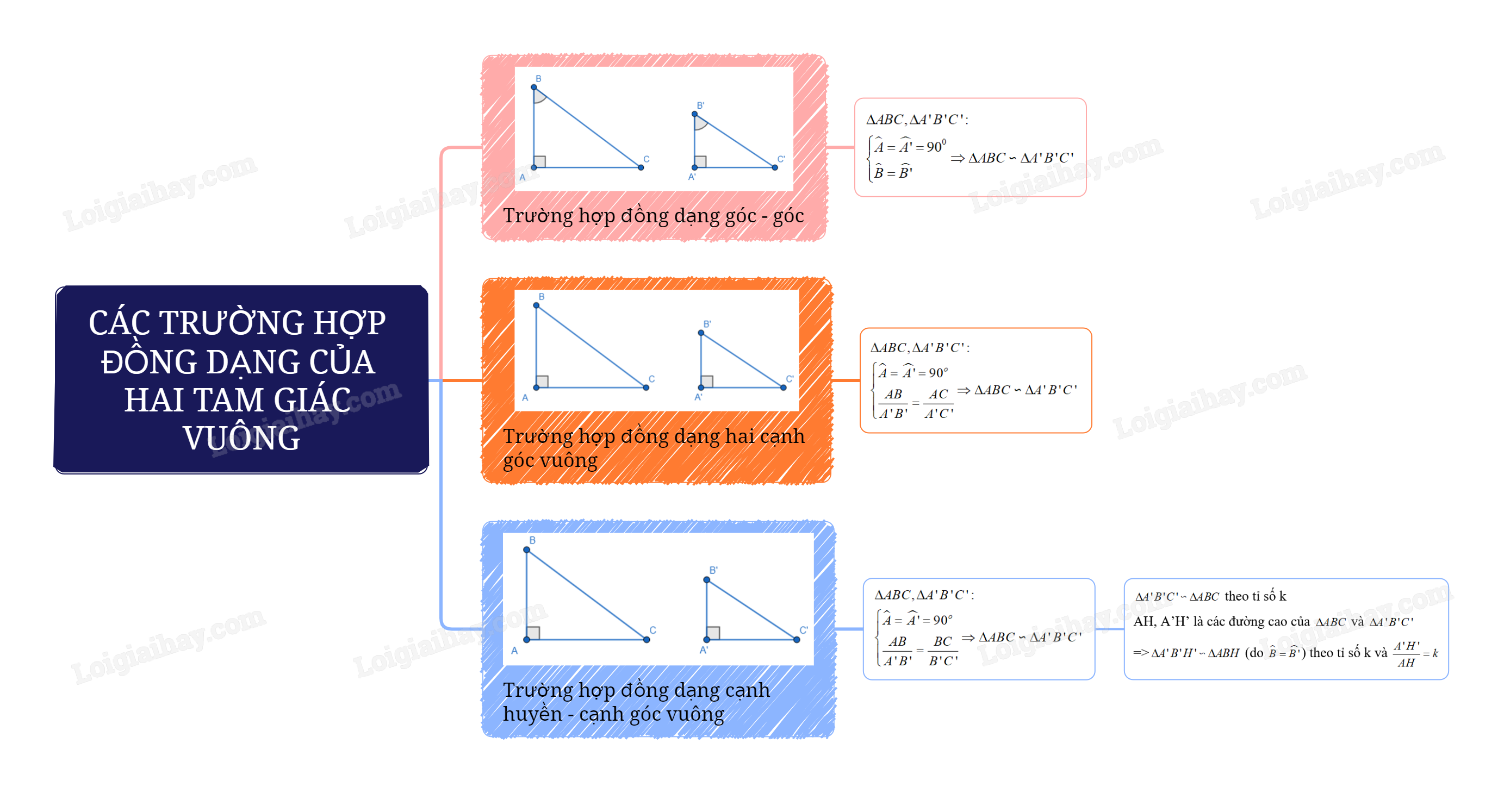
Sơ đồ tư duy Các trường hợp đồng dạng của hai tam giác vuông

Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 35: Định lí Pythagore và ứng dụng

Bài 37: Hình đồng dạng

Luyện tập chung (trang 108)

Bài tập cuối chương 9 trang 110

Bài 38: Hình chóp tam giác đều