Toán 8 Bài 35 (Kết nối tri thức): Định lí Pythagore và ứng dụng

Giải Toán 8 Bài 35: Định lí Pythagore và ứng dụng

1. Định lí Pythagora

Giải Toán 8 trang 93 Tập 2

Mở đầu trang 93 Toán 8 Tập 2: Bạn Lan vẽ một hình chữ nhật với chiều rộng và chiều dài lần lượt là 1; 3 (đơn vị độ dài). Sau đó Lan đặt lên trục số đoạn OM có độ dài bằng độ dài của đường chéo hình chữ nhật vừa vẽ (trục số nằm ngang và M nằm bên phải gốc O). Hỏi điểm M biểu diễn số thực nào? Biết rằng đơn vị độ dài trên trục số và đơn vị độ dài đo kích thước hình chữ nhật là như nhau.

Lời giải:

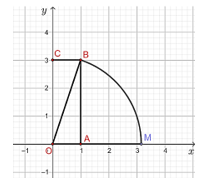
Để biết được điểm M biểu diễn số thực nào, ta cần tính độ dài đoạn thẳng OM, hay chính là tính độ dài đường chéo OB của hình chữ nhật OABC khi biết chiều dài và chiều rộng của hình chữ nhật đó, điều này dẫn đến việc cần tính độ dài cạnh huyền của tam giác vuông khi biết độ dài hai cạnh góc vuông. Để làm được điều này, ta sẽ sử dụng kiến thức của bài học hôm nay.

HĐ1 trang 93 Toán 8 Tập 2: Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3 cm, AC = 4 cm (H.9.31). Hãy đo độ dài cạnh BC và so sánh hai đại lượng AB^2 + AC^2 với BC^2.

Lời giải:

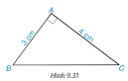
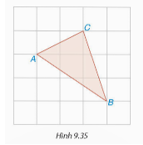
+ Đo độ dài BC ta được BC = 5 cm, vậy BC² = 25.

+ Ta có AB² = 3² = 9; AC² = 4² = 16. Vậy AB² + AC² = 25.

Vậy AB² + AC² = BC².

HĐ2 trang 93 Toán 8 Tập 2: Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a + b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32.

- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c.

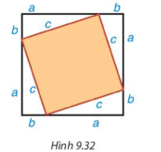
- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?

- Diện tích cả tấm bìa hình vuông cạnh a + b bằng bao nhiêu?

- So sánh c² + 2ab với (a + b)² để rút ra nhận xét về mối quan hệ giữa hai đại lượng c² và a² + b².

Lời giải:

+ Phần bìa bị che lấp là hình vuông cạnh c. Diện tích của hình vuông là c².

+ Tổng diện tích bốn tam giác vuông: 4.$\frac{1}{2}$.a.b = 2ab.

+ Diện tích tấm bìa hình vuông có cạnh bằng a + b là: (a + b)².

+ Khi đó (a + b)² = c² + 2ab, tức là a² + 2ab + b² = c² + 2ab. Suy ra c² = a² + b².

Giải Toán 8 trang 94 Tập 2

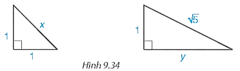
Câu hỏi trang 94 Toán 8 Tập 2: Tìm độ dài x và y trong Hình 9.34.

Lời giải:

+ Theo định lí Pythagore ta có: x² = 1² + 1² = 2. Suy ra $x=\sqrt{2}$.

+ Theo định lí Pythagore ta có: 5 = 1² + y². Suy ra y² = 5 – 1 = 4. Suy ra y = 2.

Giải Toán 8 trang 95 Tập 2

Luyện tập 1 trang 95 Toán 8 Tập 2: Trên giấy kẻ ô vuông (cạnh ô vuông bằng 1 cm), cho các điểm A, B, C như Hình 9.35. Tính độ dài các cạnh của tam giác ABC.

Lời giải:

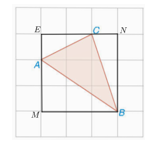
Từ A kẻ AM sao cho AM ⊥ MB như hình vẽ trên.

Từ C kẻ CN sao cho CN ⊥ NB như hình vẽ trên.

Từ C kẻ EC sao cho EC ⊥ EA như hình vẽ trên.

- Xét ΔAMB có AM ⊥ MB

Suy ra ΔAMB là tam giác vuông tại M.

Ta có: AB² = AM² + MB² (định lí Pythagore).

Khi đó AB² = 2² + 3² = 13. Suy ra AB = $\sqrt{13}$ cm.

- Xét ΔBNC có CN ⊥ NB

Suy ra ΔBNC là tam giác vuông tại N.

Ta có: BC² = NB² + NC² (định lí Pythagore).

Khi đó BC² = 3² + 1² = 10. Suy ra BC = $\sqrt{10}$ cm.

- Xét ΔAEC có EC ⊥ EA.

Suy ra ΔAEC là tam giác vuông tại E

Ta có: AC² = AE² + EC² (định lí Pythagore).

Khi đó AC² = 1² + 2² = 5. Suy ra AC = $\sqrt{5}$ cm.

Vận dụng 1 trang 95 Toán 8 Tập 2: Em hãy giải bài toán mở đầu.

Bạn Lan vẽ một hình chữ nhật với chiều rộng và chiều dài lần lượt là 1; 3 (đơn vị đo độ dài). Sau đó Lan đặt lên trục số đoạn OM có độ dài bằng độ dài đường chéo hình chữ nhật vừa vẽ (trục số nằm ngang và M nằm bên phải gốc O). Hỏi điểm M biểu diễn số thực nào? Biết rằng đơn vị độ dài đo kích thước hình chữ nhật là như nhau.

Lời giải:

Nếu điểm M biểu diễn cho số thực x thì đoạn thẳng OM có độ dài x (đơn vị độ dài).

Đoạn thẳng OM là cạnh huyền của một tam giác vuông với hai cạnh góc vuông là hai cạnh của hình chữ nhật.Theo định lí Pythagore ta có x² = 1² + 3² = 10. Suy ra $x=\sqrt{10}$

Vậy điểm M biểu diễn số thực $\sqrt{10}$ .

2. Ứng dụng định lí Pythagora

Luyện tập 2 trang 95 Toán 8 Tập 2: Cho tam giác vuông với kích thước như Hình 9.37. Hãy tính độ dài x và cho biết những tam giác nào đồng dạng, viết đúng kí hiệu đồng dạng.

Lời giải:

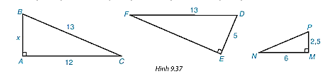
Tam giác ABC vuông tại A nên theo định lí Pythagore ta có: AB² + AC² = BC².

Hay x² + 12² = 13². Suy ra x² =13² – 12² = 25. Suy ra x = 5.

Vậy ∆ABC = ∆EDF (cạnh huyền – cạnh góc vuông).

Khi đó ∆ABC ∽ ∆EDF. (1)

Lại có $\frac{AB}{MP}=\frac{AC}{MN}=2;\widehat{BAC}=\widehat{NMP}=90°$ .

Do đó: ∆ABC ∽ ∆MPN (c.g.c). (2)

Từ (1) và (2) suy ra ∆MPN ∽ ∆EDF.

Giải Toán 8 trang 96 Tập 2

Vận dụng 2 trang 96 Toán 8 Tập 2: Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3 km đến điểm B thì rẽ vuông góc sang trái, chạy được 3 km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1 km nữa thì gặp người khách tại điểm D (H.9.38). Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là bao nhiêu kilômét?

Lời giải:

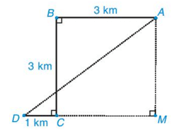
Có BC = AM = AB = CM = 3 km (do AMCB là hình vuông).

Suy ra MD = CM + CD = 3 + 1 = 4 (km).

Xét tam giác AMD vuông tại M, theo định lí Pythagore, ta có:

AD² = AM² + MD² = 3² + 4² = 25. Suy ra AD = 5 km.

Vậy lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là 5 km.

Câu hỏi trang 96 Toán 8 Tập 2: Cho Hình 9.40, trong các đoạn thẳng AC, AD, AE đoạn nào có độ dài lớn nhất, đoạn nào có độ dài nhỏ nhất?

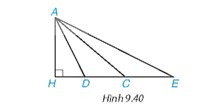
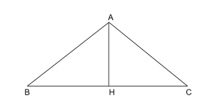
Lời giải:

Áp dụng định lí Pythagore trong tam giác AHD vuông tại H có:

AD² = AH² + HD² (1)

Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có:

AC² = AH² + HC² (2)

Áp dụng định lí Pythagore trong tam giác AHE vuông tại H có:

AE² = AH² + HE² (3)

Vì HE > HC > HD suy ra HE² > HC² > HD². (4)

Từ (1), (2), (3), (4) suy ra: AE² > AC² > AD² ⇒ AE > AC > AD.

Vậy đoạn AE là lớn nhất, đoạn AD là nhỏ nhất.

Luyện tập 3 trang 96 Toán 8 Tập 2: Trước đây chúng ta thừa nhận định lí về trường hợp bằng nhau đặc biệt của hai tam giác vuông: “Nếu một cạnh góc vuông và cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và cạnh huyền của tam giác vuông kia thì hai tam giác vuông đó bằng nhau”. Áp dụng định lí Pythagore, em hãy chứng minh định lí trên.

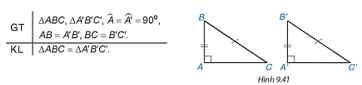
Lời giải:

- Xét tam giác ABC vuông tại A, có

BC² = AB² + AC² (định lí Pythagore) (1)

- Xét tam giác A'B'C' vuông tại A' có:

B′C′² = A′B′² + A′C′² (định lí Pythagore) (2)

Mà AB = A′B′, BC = B′C′ (3)

Từ (1), (2), (3) suy ra AC = A′C′.

Suy ra hai tam giác đã cho bằng nhau theo trường hợp cạnh – cạnh – cạnh.

Giải Toán 8 trang 97 Tập 2

Thử thách nhỏ trang 97 Toán 8 Tập 2: Tính chiều cao theo đơn vị centimét của một tam giác đều cạnh 2 cm (H.9.42) (làm tròn kết quả đến chữ số thập phân thứ hai).

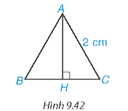
Lời giải:

Vì tam giác ABC là tam giác đều, AH ⊥ BC nên H là trung điểm của BC, suy ra

HB = HC = $\frac{BC}{2}=\frac{2}{2}=1$ (cm).

Áp đụng định lí Pythagore trong tam giác vuông AHC ta có:

AC² = AH² + HC² ⇒ AH² = AC² − HC² = 2² − 1² = 3 ⇒ AH = $\sqrt{3}$ ≈ 1,73 (cm).

Vậy chiều cao của tam giác đều khoảng 1,73 cm.

Bài tập

Bài 9.17 trang 97 Toán 8 Tập 2: Cho tam giác ABC vuông tại A. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai ?

a) AB² + BC² = AC².

b) BC² − AC² = AB².

c) AC² + BC² = AB².

d) BC² − AB² = AC².

Lời giải:

Tam giác ABC vuông tại A thì BC là cạnh huyền.

Khi đó, theo định lí Pythagore, ta có BC² = AB² + AC², suy ra BC² – AC² = AB² hay BC² − AB² = AC².

Do đó b) và d) là khẳng định đúng; a) và c) là khẳng định sai.

Bài 9.18 trang 97 Toán 8 Tập 2: Những bộ ba số đo nào dưới đây là độ dài ba cạnh của một tam giác vuông?

a) 1 cm, 1 cm, 2 cm.

b) 2 cm, 4 cm, 20 cm.

c) 5 cm, 4 cm, 3 cm.

d) 2 cm, 2 cm, $2\sqrt{2}$ cm.

Lời giải:

Do 1 + 1 = 2 và 2 + 4 = 6 < 20 nên các bộ ba trong a) , b) đều không thỏa mãn bất đẳng thức tam giác nên không thể là độ dài ba cạnh của một tam giác.

Vì 5² = 3² + 4² và ${\left(2\sqrt{2}\right)}^2=2^2+2^2$ nên các bộ ba trong c), d) là độ dài ba cạnh của tam giác vuông (theo định lí Pythagore đảo).

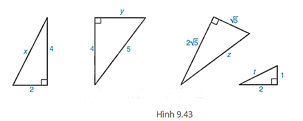
Bài 9.19 trang 97 Toán 8 Tập 2: Tính độ dài x, y, z, t trong Hình 9.43.

Lời giải:

Các tam giác trong Hình 9.43 đều là các tam giác vuông nên ta áp dụng định lí Pythagore.

+) x² = 4² + 2² = 20. Suy ra x = $2\sqrt{5}$.

+) 5² = 4² + y² nên y² = 5² − 4² = 9. Suy ra y = 3.

+) z² =${\left(\sqrt{5}\right)}^2+{\left(2\sqrt{5}\right)}^2$ = 25. Suy ra z = 5.

+) t² = 1² + 2² = 5. Suy ra t = $\sqrt{5}$ .

Bài 9.20 trang 97 Toán 8 Tập 2: Cho tam giác ABC cân tại đỉnh A, chiều cao AH = 3 cm và cạnh đáy BC = 10 cm. Hãy tính độ dài các cạnh bên AB, AC.

Lời giải:

Vì tam giác ABC cân tại A có đường cao AH nên AH cũng là đường trung tuyến hay H là trung điểm BC. Suy ra HB = HC = BC : 2 = 10 : 2 = 5 cm.

Xét tam giác AHB vuông tại H, theo định lí Pythagore ta có

AB² = AH² + HB² = 3² + 5² = 34.

Suy ra AB = $\sqrt{34}$ cm.

Do tam giác ABC cân tại A nên AC = AB = $\sqrt{34}$ cm.

Bài 9.21 trang 97 Toán 8 Tập 2: Hãy tính diện tích của một hình chữ nhật có chiều rộng 8 cm và đường chéo dài 17 cm.

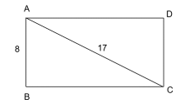
Lời giải:

Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta có: AB² + BC² = AC².

Suy ra BC² = AC² – AB² = 17² – 8² = 225.

Do đó, BC = 15 (cm).

Diện tích của hình chữ nhật là: AB . BC = 8 . 15 = 120 (cm²).

Bài 9.22 trang 97 Toán 8 Tập 2: Chú cún bị xích bởi một sợi dây dài 6 m để canh một mảnh vườn giới hạn bởi các điểm A, B, E, F, D trong hình vuông ABCD có cạnh 5 m như Hình 9.44. Đầu xích buộc cố định tại điểm A của mảnh vườn. Hỏi chú cún có thể chạy đến tất cả các điểm của mảnh vườn mình phải canh không?

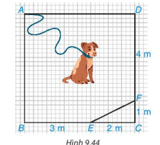
Lời giải:

- Áp dụng định lí Pythagore cho tam giác ABE vuông tại B, có

AE² = AB² + BE² = 5² + 3² = 34.

Suy ra AE = $\sqrt{34}$ m < 6 m.

Suy ra chú cún có thể chạy đến điểm E do khoảng cách AE ngắn hơn sợi dây.

- Áp dụng định lí Pythagore cho tam giác ADF vuông tại D, có

AF² = AD² + DF² = 5² + 4² = 41.

Suy ra AE = $\sqrt{41}$ m > 6 m.

Suy ra chú cún không thể chạy đến điểm F do khoảng cách AF dài hơn sợi dây.

- Áp dụng định lí Pythagore cho tam giác ADC vuông tại D, có

AC² = AD² + DC² = 5² + 5² = 50.

Suy ra AE = $5\sqrt{2}$ m > 6 m.

Suy ra chú cún không thể chạy đến điểm C do khoảng cách AC dài hơn sợi dây.

Vậy chú cún không thể chạy hết tất cả các điểm của mảnh vườn. Chú chó chỉ có thể chạy đến điểm B, D, E.

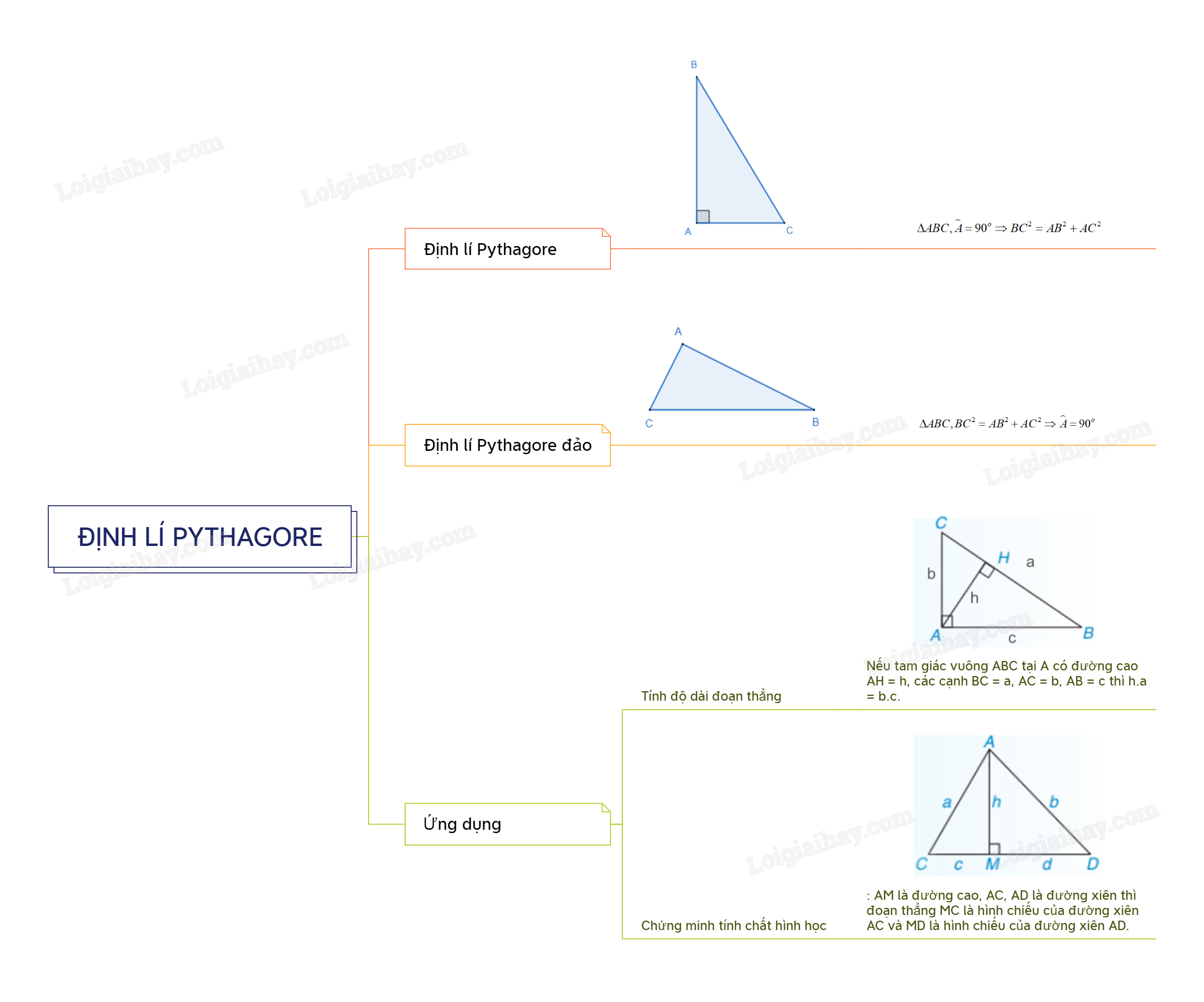
Lý thuyết Định lí Pythagore và ứng dụng

1. Định lí Pythagore

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

$\mathrm{\Delta }ABC,\hat{A}={90}^o\Rightarrow B{C}^2=A{B}^2+A{C}^2$

Ví dụ:

Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do $3^2+4^2=5^2$, suy ra $B{C}^2=A{B}^2+A{C}^2$.

2. Định lí Pythagore đảo

Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

$\mathrm{\Delta }ABC,B{C}^2=A{B}^2+A{C}^2\Rightarrow \hat{A}={90}^o$

3. Ứng dụng của định lí Pythagore

a. Tính độ dài đoạn thẳng

Nhận xét: Nếu tam giác vuông ABC tại A có đường cao AH = h, các cạnh BC = a, AC = b, AB = c thì h.a = b.c.

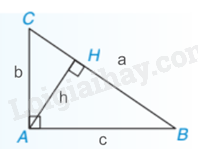
Ví dụ: Tam giác ABC vuông tại A có AB = 5cm, AC = 12cm thì BC = $\sqrt{5^2+{12}^2}=\sqrt{169}=13$

b. Chứng minh tính chất hình học

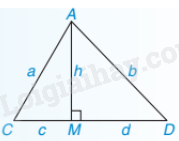
Chú ý: AM là đường cao, AC, AD là đường xiên thì đoạn thẳng MC là hình chiếu của đường xiên AC và MD là hình chiếu của đường xiên AD.

Sơ đồ tư duy Định lí Pythagore và ứng dụng

Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung (trang 91)

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng

Luyện tập chung (trang 108)

Bài tập cuối chương 9 trang 110