Tại một bể bơi có dạng hình tròn có đường kính AB = 10m, một người xuất phát từ A

Lời giải Bài 12 trang 95 SBT Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

1 671 07/11/2023

Trang trước

Trang sau

Giải SBT Toán 11 Bài tập cuối chương 3 trang 91

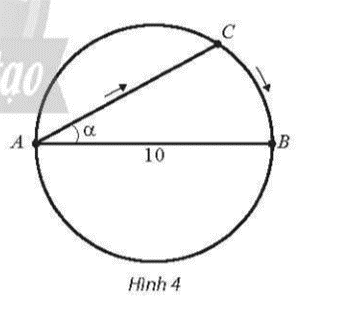
Bài 12 trang 95 SBT Toán 11 Tập 1: Tại một bể bơi có dạng hình tròn có đường kính AB = 10 m, một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc $α (0 < α < \frac{π}{2}),$ rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi S(α) là quãng đường người đó đã di chuyển.

Tại một bể bơi có dạng hình tròn có đường kính AB = 10m, một người xuất phát

a) Viết công thức tính S(α) theo $α (0 < α < \frac{π}{2})$ .

b) Xét tính liên tục của hàm số y = S(α) trên khoảng $(0; \frac{π}{2})$ .

c) Tính các giới hạn $\lim_{x \to 0^{+}} S (α)$ và $\lim_{x \to {\frac{π}{2}}^{+}} S (α) .$

Lời giải:

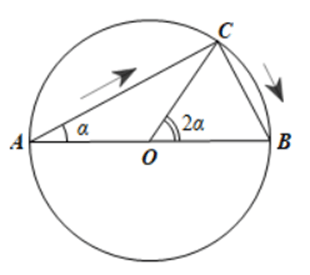
Kí hiệu O là tâm hình tròn.

Tại một bể bơi có dạng hình tròn có đường kính AB = 10m, một người xuất phát

a) Do tam giác ABC vuông tại C nên AC = ABcosα = 10cosα (m).

Ta có $\hat{BOC} = 2 \hat{BAC} = 2 α$ .

Suy ra độ dài cung CB là $l = OB . \hat{BOC} = 5 .2 α = 10 α (m)$ .

Quãng đường di chuyển (tính theo m) của người đó là:

$S (α) = AC + l = 10 cos α + 10 α = 10 (α + cos α) (0 < α < \frac{π}{2})$

b) Do các hàm số y = α và y = cosα liên tục trên ℝ nên hàm số y = S(α) liên tục trên ℝ

Mà $(0; \frac{π}{2}) \subset ℝ$ nên hàm số y = S(α) liên tục trên $(0; \frac{π}{2}) .$

c) Ta có:

$\lim_{α \to 0^{+}} S (α) = \lim_{α \to 0^{+}} 10 (α + cos α) = 10 \cdot (0 + cos 0) = 10 \cdot (0 + 1) = 10;$

$lim_{α \to {\frac{π}{2}}^{+}} S (α) = lim_{α \to {\frac{π}{2}}^{+}} 10 (α + cos α)$ $= 10 \cdot (\frac{π}{2} + cos \frac{π}{2}) = 10 \cdot (\frac{π}{2} + 0) = 5 π .$

Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Câu 1 trang 91 SBT Toán 11 Tập 1: $lim \frac{3 n^{2} + 2 n}{2 - n^{2}}$ bằng...

Câu 2 trang 92 SBT Toán 11 Tập 1: $lim \frac{\sqrt{4 n^{2} + 4 n + 1}}{4 n + 1}$ bằng...

Câu 3 trang 92 SBT Toán 11 Tập 1: $lim \frac{2 n + 1}{\sqrt{9 n^{2} + 1} - n}$ bằng...

Câu 4 trang 92 SBT Toán 11 Tập 1: Cho hai dãy số (u_n) và (v_n) thoả mãn limu_n = 4, lim(v_n – 3) = 0....

Câu 5 trang 92 SBT Toán 11 Tập 1: $lim \frac{4^{n}}{2 \cdot 4^{n} + 3^{n}}$ bằng...

Câu 6 trang 92 SBT Toán 11 Tập 1: $\lim_{x \to 2} \frac{x^{2} - x - 2}{2 x - 4}$ bằng...

Câu 7 trang 92 SBT Toán 11 Tập 1: $\lim_{x \to 1} \frac{2 x - 2}{\sqrt{x + 3} - 2}$ bằng...

Câu 8 trang 92 SBT Toán 11 Tập 1: Biết $\lim_{x \to 1} \frac{x^{2} - 3 x + a}{x - 1} = b$ với a và b là hai số thực. Giá trị của a + b bằng...

Câu 9 trang 92 SBT Toán 11 Tập 1: Cho hàm số $f (x) = \frac{x^{2} - 3 x}{|x - 3|} .$ Đặt $a = \lim_{x \to 3^{+}} f (x)$ và $b = \lim_{x \to 3^{-}} f (x) .$ ...

Câu 10 trang 92 SBT Toán 11 Tập 1: Biết rằng $\lim_{x \to + \infty} f (x) = 2, \lim_{x \to + \infty} (f (x) + 2 g (x)) = 4$ ....

Câu 11 trang 93 SBT Toán 11 Tập 1: Biết rằng $\lim_{x \to + \infty} \frac{2 ax}{\sqrt{x^{2} + ax} + x} = 3 .$ Giá trị của a là...

Câu 12 trang 93 SBT Toán 11 Tập 1: $\lim_{x \to - 2^{-}} \frac{1 - 3 x}{x + 2}$ bằng...

Câu 13 trang 93 SBT Toán 11 Tập 1: Biết rằng hàm số...

Câu 14 trang 93 SBT Toán 11 Tập 1: Cho hàm số $f (x) = \{\begin{cases} \tan x k h i 0 \leq x \leq \frac{π}{4} \\ k - c o t x k h i \frac{π}{4} < x \leq \frac{π}{2} \end{cases}$ liên tục...

Câu 15 trang 93 SBT Toán 11 Tập 1: Biết rằng phương trình x³ ‒ 2x ‒3 = 0 chỉ có một nghiệm....

Bài 1 trang 93 SBT Toán 11 Tập 1: Tìm các giới hạn sau: a) $lim \frac{n (2 n^{2} + 3)}{4 n^{3} + 1}$ ;...

Bài 2 trang 93 SBT Toán 11 Tập 1: Cho các dãy số (u_n) và (v_n) thoả mãn limu_n = 2, lim(u_n– v_n) = 4...

Bài 3 trang 93 SBT Toán 11 Tập 1: Tìm $\lim \frac{6^{n} + 4^{n}}{(2^{n} + 1) (3^{n} + 1)}$ ....

Bài 4 trang 94 SBT Toán 11 Tập 1: Cho a > b > 0 và $lim \frac{a^{n + 1} + b^{n}}{2 a^{n} + b^{n + 1}} = 1 .$ Tìm giá trị của a....

Bài 5 trang 94 SBT Toán 11 Tập 1: Cho dãy số (u_n) thoả mãn ${limnu}_{n} = \frac{1}{2} .$ Tìm lim(3n – 4)u_n....

Bài 6 trang 94 SBT Toán 11 Tập 1: Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:...

Bài 7 trang 94 SBT Toán 11 Tập 1: Biết rằng, từ vị trí A, một mũi tên bay với tốc độ 10m/s hướng thẳng tới bia mục tiêu đặt ở vị trí B...

Bài 8 trang 94, 95 SBT Toán 11 Tập 1: Cho hàm số $f (x) = \{\begin{matrix} \frac{x^{2} - 9}{|x + 3|} & khi x \neq - 3 \\ a & khi x = - 3. \end{matrix}$ ...

Bài 9 trang 95 SBT Toán 11 Tập 1: Cho hàm số $f (x) = \frac{2 x + 1}{x - 3}$ . a) Xét tính liên tục của hàm số đã cho....

Bài 10 trang 95 SBT Toán 11 Tập 1: Cho điểm M thay đổi trên parabol y = x²; H là hình chiếu vuông góc của M trên trục hoành...

Bài 11 trang 95 SBT Toán 11 Tập 1: Chứng minh rằng phương trình x⁵ + 3x² ‒ 1 = 0 trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1) đều có ít nhất một nghiệm....

Bài 12 trang 95 SBT Toán 11 Tập 1: Tại một bể bơi có dạng hình tròn có đường kính AB = 10 m....

Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song

Bài 5: Phép chiếu song song

1 671 07/11/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: