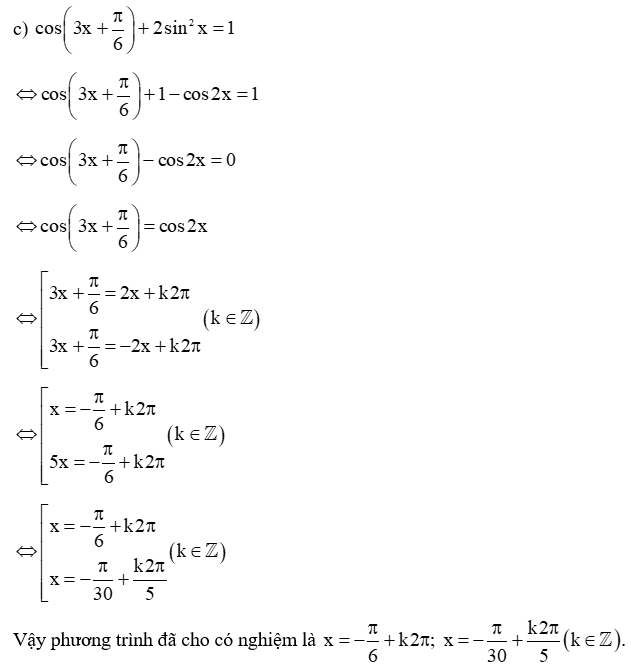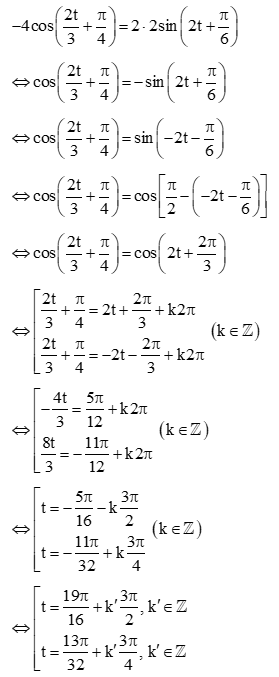Sách bài tập Toán 11 (Chân trời sáng tạo) Bài tập cuối chương 1 trang 32

Giải SBT Toán 11 Bài tập cuối chương 1 trang 32

A. TRẮC NGHIỆM

Câu 1 trang 32 SBT Toán 11 Tập 1: Trên đường tròn lượng giác, góc lượng giác $\frac{13\pi }{7}$ có cùng điểm biểu diễn với góc lượng giác nào sau đây?

A. $\frac{6\pi }{7}.$

B. $\frac{20\pi }{7}.$

C. $-\frac{\pi }{7}.$

D. $\frac{19\pi }{14}.$

Lời giải:

Đáp án đúng là: C

Trên đường tròn lượng giác, các góc lượng giác có cùng điểm biểu diễn với $\frac{13\pi }{7}$ có dạng $\frac{13\pi }{7}+k2\pi ,k\in \mathbb{Z}.$

Ta thấy $-\frac{\pi }{7}=\frac{13\pi }{7}-2\pi$ nên góc lượng giác $\frac{13\pi }{7}$ và $-\frac{\pi }{7}$ có cùng điểm biểu diễn.

Câu 2 trang 32 SBT Toán 11 Tập 1: Điểm biểu diễn trên đường tròn lượng giác của góc lượng giác có số đo ‒830° thuộc góc phần tư thứ mấy?

A. Góc phần tư thứ I.

B. Góc phần tư thứ II.

C. Góc phần tư thứ III.

D. Góc phần tư thứ IV.

Lời giải:

Đáp án đúng là: C

Ta có ‒830° = ‒110° – 2.360°, mà ‒180° < ‒110° < ‒90° nên điểm biểu diễn trên đường tròn lượng giác của góc lượng giác có số đo ‒830° thuộc góc phần tư thứ III.

Câu 3 trang 32 SBT Toán 11 Tập 1: Trong các khẳng định sau, khẳng định nào là sai?

A. cos(π ‒ x) = ‒cosx.

B.$\sin \left(\frac{\pi }{2}-x\right)=-\cos x.$

C. tan(π + x) = tanx.

D. $\cos \left(\frac{\pi }{2}-x\right)=\sin x.$

Lời giải:

Đáp án đúng là: B

Ta có $\sin \left(\frac{\pi }{2}-x\right)=\cos x,$ do đó khẳng định B là sai.

Câu 4 trang 33 SBT Toán 11 Tập 1: Cho $\cos \alpha =\frac{1}{3}.$ Trong các đẳng thức sau, đẳng thức nào không thể xảy ra?

A. $\sin \alpha =-\frac{2\sqrt{2}}{3}.$

B. $\cos 2\alpha =\frac{2\sqrt{2}}{9}.$

C. $\cot \alpha =\frac{\sqrt{2}}{4}.$

D. $\cos \frac{\alpha }{2}=\frac{\sqrt{6}}{3}.$

Lời giải:

Đáp án đúng là: B

Ta có $\cos 2\alpha =2{\cos }^2\alpha -1$ = $2\cdot {\left(\frac{1}{3}\right)}^2-1=2\cdot \frac{1}{9}-1=-\frac{7}{9}.$

Do đó đẳng thức ở phương án B là sai.

Câu 5 trang 33 SBT Toán 11 Tập 1: Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. y = tanx ‒ 2cotx.

B. $y=\sin \frac{5\pi -x}{2}.$

C. y = 3sin²x + cos2x.

D. $y=\cot \left(2x+\frac{\pi }{5}\right).$

Lời giải:

Đáp án đúng là: A

Xét hàm số y = f(x) = tanx ‒ 2cotx có tập xác định $D=ℝ\backslash \left\{k\pi ;\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right\}.$

Với mọi x ∈ D thì –x ∈ D và:

f(–x) = = tan(–x) ‒ 2cot(–x) = –tanx + 2cotx = –(tanx – 2cotx) = –f(x).

Vậy hàm số y = f(x) = tanx ‒ 2cotx là hàm số lẻ.

Câu 6 trang 33 SBT Toán 11 Tập 1: Trong các hàm số sau, hàm số nào nghịch biến trên khoảng $\left(0;\frac{\pi }{2}\right)?$

A. y = sinx.

B. y = ‒cotx.

C. y = tanx.

D. y = cosx.

Lời giải:

Đáp án đúng là: D

Hàm số y = cosx nghịch biến trên khoảng (k2π; π + k2π) (k ∈ ℤ).

Ta thấy $\left(0;\frac{\pi }{2}\right)\subset \left(0;\pi \right)$ nên hàm số y = cosx nghịch biến trên khoảng $\left(0;\frac{\pi }{2}\right).$

Câu 7 trang 33 SBT Toán 11 Tập 1: Cho $\sin \alpha =-\frac{3}{5}$ và $\cos \alpha =\frac{4}{5}.$ Trong các đẳng thức sau, đẳng thức nào đúng?

A. $\sin \left(\alpha +\frac{\pi }{4}\right)=\frac{\sqrt{2}}{10}.$

B. $\sin 2\alpha =-\frac{12}{25}.$

C. $\tan \left(2\alpha +\frac{\pi }{4}\right)=-\frac{31}{17}.$

D. $\cos \left(\alpha +\frac{\pi }{3}\right)=\frac{3+4\sqrt{3}}{10}.$

Lời giải:

Đáp án đúng là: A

Ta có: $\sin \left(\alpha +\frac{\pi }{4}\right)=\sin \alpha \cos \frac{\pi }{4}+\cos \alpha \sin \frac{\pi }{4}$

= $\sin \alpha \cdot \frac{\sqrt{2}}{2}+\cos \alpha \cdot \frac{\sqrt{2}}{2}$

= $\left(-\frac{3}{5}\right)\cdot \frac{\sqrt{2}}{2}+\frac{4}{5}\cdot \frac{\sqrt{2}}{2}=\frac{-3\sqrt{2}}{10}+\frac{4\sqrt{2}}{10}=\frac{\sqrt{2}}{10}.$

Vậy ta chọn phương án A.

Câu 8 trang 33 SBT Toán 11 Tập 1: Cho $\sin \alpha =\frac{\sqrt{15}}{4}$ và $\cos \beta =\frac{1}{3}.$ Giá trị của biểu thức sin(α + β)sin(α ‒ β) bằng

A. $\frac{7}{12}.$

B. $\frac{1}{12}.$

C. $\frac{\sqrt{15}}{12}.$

D. $\frac{7}{144}.$

Lời giải:

Đáp án đúng là: D

Ta có: $\cos 2\alpha =1-2{\sin }^2\alpha =1-2\cdot {\left(\frac{\sqrt{15}}{4}\right)}^2=-\frac{7}{8};$

$\cos 2\beta =2{\cos }^2\beta -1=2\cdot {\left(\frac{1}{3}\right)}^2-1=-\frac{7}{9}.$

Khi đó sin(α + β)sin(α ‒ β)

$=\frac{1}{2}\left[\cos \left(\alpha +\beta -\alpha +\beta \right)-\cos \left(\alpha +\beta +\alpha -\beta \right)\right]$

$=\frac{1}{2}\left[\cos \left(2\beta \right)-\cos \left(2\alpha \right)\right]$

$=\frac{1}{2}\left[-\frac{7}{9}-\left(-\frac{7}{8}\right)\right]=\frac{1}{2}\cdot \frac{7}{72}=\frac{7}{144}.$

Câu 9 trang 33 SBT Toán 11 Tập 1: Số nghiệm của phương trình $\sin \left(2x+\frac{\pi }{3}\right)=\frac{1}{2}$ trên đoạn [0; 8π] là

A. 14.

B. 15.

C. 16.

D. 17.

Lời giải:

Đáp án đúng là: C

$\sin \left(2x+\frac{\pi }{3}\right)=\frac{1}{2}$

$\iff \sin \left(2x+\frac{\pi }{3}\right)=\sin \frac{\pi }{6}$

$\iff 2x+\frac{\pi }{3}=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $2x+\frac{\pi }{3}=\pi -\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{\pi }{12}+k\pi ,k\in \mathbb{Z}$ hoặc $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$

Trường hợp 1: $x=-\frac{\pi }{12}+k\pi \left(k\in \mathbb{Z}\right)$ và x ∈ [0; 8π]

Suy ra $0\le -\frac{\pi }{12}+k\pi \le 8\pi$

$\iff \frac{1}{12}\le k\le \frac{97}{12}$

Mà k ∈ ℤ nên k ∈ {1; 2; …; 8}

Do đó trong trường hợp này, phương trình có 8 nghiệm trên đoạn [0; 8π].

Trường hợp 2: $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$ và x ∈ [0; 8π]

Suy ra $0\le \frac{\pi }{4}+k\pi \le 8\pi$

$\iff \frac{-1}{4}\le k\le \frac{31}{4}$

Mà k ∈ ℤ nên k ∈ {0; 1; 2; …; 7}

Do đó trong trường hợp này, phương trình có 8 nghiệm trên đoạn [0; 8π].

Vậy số nghiệm của phương trình $\sin \left(2x+\frac{\pi }{3}\right)=\frac{1}{2}$ trên đoạn [0; 8π] là: 8 + 8 =16 nghiệm.

Câu 10 trang 33 SBT Toán 11 Tập 1: Số nghiệm của phương trình $\tan \left(\frac{\pi }{6}-x\right)=\tan \frac{3\pi }{8}$ trên đoạn [‒6π; π] là:

A. 7.

B. 8.

C. 9.

D. 10.

Lời giải:

Đáp án đúng là: A

$\tan \left(\frac{\pi }{6}-x\right)=\tan \frac{3\pi }{8}$

$\iff \frac{\pi }{6}-x=\frac{3\pi }{8}+k\pi ,k\in \mathbb{Z}$

$\iff x=\frac{\pi }{6}-\frac{3\pi }{8}-k\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{5\pi }{24}+k^{\text{'}}\pi ,k^{\text{'}}\in \mathbb{Z}$

Do nghiệm của phương trình nằm trên đoạn [‒6π; π] nên ta có:

$-6\pi \le -\frac{5\pi }{24}+k^{\text{'}}\pi \le \pi$

$\iff -\frac{139}{24}\le k^{\text{'}}\le \frac{29}{24}$

Mà k' ∈ ℤ nên k' ∈ {‒5; ‒4; ‒3; ‒2; ‒1; 0; 1}

Vậy phương trình $\tan \left(\frac{\pi }{6}-x\right)=\tan \frac{3\pi }{8}$ có 7 nghiệm trên đoạn [‒6π; π].

B. TỰ LUẬN

Bài 1 trang 34 SBT Toán 11 Tập 1: Cho $\sin \alpha =\frac{3}{4}$ với $\frac{\pi }{2}<\alpha <\pi .$ Tính giá trị của các biểu thức sau:

a) sin2α;

b) $\cos \left(\alpha +\frac{\pi }{3}\right);$

c) $\tan \left(2\alpha -\frac{\pi }{4}\right).$

Lời giải:

a) Vì $\frac{\pi }{2}<\alpha <\pi$ nên cosα < 0.

Ta có sin²α + cos²α = 1, suy ra cos²α = 1 – sin²α

Do đó $\cos \alpha =-\sqrt{1-{\sin }^2\alpha }=-\sqrt{1-{\left(\frac{3}{4}\right)}^2}=-\frac{\sqrt{7}}{4}$

Ta có: sin2α = 2sinαcosα $=2\cdot \frac{3}{4}\cdot \left(-\frac{\sqrt{7}}{4}\right)=-\frac{3\sqrt{7}}{8}.$

b) $\cos \left(\alpha +\frac{\pi }{3}\right)=\cos \alpha \cos \frac{\pi }{3}-\sin \alpha \sin \frac{\pi }{3}$

$=\frac{-\sqrt{7}}{4}\cdot \frac{1}{2}-\frac{3}{4}\cdot \frac{\sqrt{3}}{2}=\frac{-\sqrt{7}-3\sqrt{3}}{8}.$

c) $\frac{\sin \alpha }{\cos \alpha }=\frac{\frac{3}{4}}{-\frac{\sqrt{7}}{4}}=-\frac{3}{\sqrt{7}}$

$\tan \left(2\alpha -\frac{\pi }{4}\right)=\frac{\tan 2\alpha -\tan \frac{\pi }{4}}{1+\tan 2\alpha \tan \frac{\pi }{4}}$

Mà $\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha }=\frac{2\frac{\sin \alpha }{\cos \alpha }}{1-{\left(\frac{\sin \alpha }{\cos \alpha }\right)}^2}=\frac{2\cdot \frac{-3}{\sqrt{7}}}{1-{\left(\frac{-3}{\sqrt{7}}\right)}^2}=3\sqrt{7}$

Nên $\tan \left(2\alpha -\frac{\pi }{4}\right)=\frac{\tan 2\alpha -\tan \frac{\pi }{4}}{1+\tan 2\alpha \tan \frac{\pi }{4}}$

$=\frac{3\sqrt{7}-1}{1+3\sqrt{7}\cdot 1}=\frac{3\sqrt{7}-1}{3\sqrt{7}+1}=\frac{{\left(3\sqrt{7}-1\right)}^2}{\left(3\sqrt{7}+1\right)\left(3\sqrt{7}-1\right)}$

$=\frac{63-6\sqrt{7}+1}{63-1}=\frac{64-6\sqrt{7}}{62}=\frac{32-3\sqrt{7}}{31}.$

Bài 2 trang 34 SBT Toán 11 Tập 1: Chứng minh rằng các hàm số dưới đây là hàm số tuần hoàn và xét tính chẵn, lẻ của mỗi hàm số đó.

a) $y=3\sin x+2\tan \frac{x}{3};$

b) $y=\cos x\sin \frac{\pi -x}{2}.$

Lời giải:

a) Hàm số $y=3\sin x+2\tan \frac{x}{3}$ xác định khi $\cos \frac{x}{3}\ne 0$

$\iff \frac{x}{3}\ne \frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ $\iff x\ne \frac{3\pi }{2}+k3\pi \left(k\in \mathbb{Z}\right)$

Tập xác định của hàm số $y=3\text{sin}x+2\text{tan}\frac{x}{3}$ là $D=ℝ\backslash \left\{\frac{3\pi }{2}+k3\pi \mid k\in \mathbb{Z}\right\}.$

⦁ Vì x ± 6π ∈ D với mọi x ∈ D và

$3\text{sin}\left(x+6\pi \right)+2\text{tan}\frac{x+6\pi }{3}$ = $3\text{sin}x+2\text{tan}\left(\frac{x}{3}+2\pi \right)$ = $3\text{sin}x+2\text{tan}\frac{x}{3}$

Nên hàm số $y=3\text{sin}x+2\text{tan}\frac{x}{3}$ là hàm số tuần hoàn.

⦁ Vì ‒x ∈ D với mọi x ∈ D và

$3\text{sin}\left(-x\right)+2\text{tan}\left(-\frac{x}{3}\right)$ = $-3\text{sin}x-2\text{tan}\frac{x}{3}=-\left(3\text{sin}x+2\text{tan}\frac{x}{3}\right)$

Nên hàm số $y=3\text{sin}x+2\text{tan}\frac{x}{3}$ là hàm số lẻ.

b) Hàm số $y=\text{cos}x\text{sin}\frac{\pi -x}{2}$ có tập xác định là ℝ.

⦁ Vì x ± 4π ∈ ℝ với mọi x ∈ ℝ và

$\text{cos}\left(x+4\pi \right)\text{sin}\frac{\pi -\left(x+4\pi \right)}{2}$ = $\text{cos}x\text{sin}\left(\frac{\pi -x}{2}-2\pi \right)=\text{cos}x\text{sin}\frac{\pi -x}{2}$

Nên hàm số $y=\text{cos}x\text{sin}\frac{\pi -x}{2}$ là hàm số tuần hoàn.

⦁ Vì ‒x ∈ ℝ với mọi x ∈ ℝ và

$\text{cos}\left(-x\right)\text{sin}\frac{\pi +x}{2}$ = $\text{cos}x\text{sin}\left(\pi -\frac{\pi -x}{2}\right)=\text{cos}x\text{sin}\frac{\pi -x}{2}$

Nên hàm số $y=\text{cos}x\text{sin}\frac{\pi -x}{2}$ là hàm số chẵn.

Bài 3 trang 34 SBT Toán 11 Tập 1: Chứng minh các đẳng thức lượng giác sau:

a) ${\sin }^2\left(x+\frac{\pi }{8}\right)-{\sin }^2\left(x-\frac{\pi }{8}\right)=\frac{\sqrt{2}}{2}\sin 2x;$

b) sin²y + 2cosxcosycos(x ‒ y) = cos²x + cos²(x ‒ y).

Lời giải:

a) ${\text{sin}}^2\left(x+\frac{\pi }{8}\right)-{\text{sin}}^2\left(x-\frac{\pi }{8}\right)$

$=\left[\text{sin}\left(x+\frac{\pi }{8}\right)+\text{sin}\left(x-\frac{\pi }{8}\right)\right]\left[\text{sin}\left(x+\frac{\pi }{8}\right)-\text{sin}\left(x-\frac{\pi }{8}\right)\right]$

$=\left(2\text{sin}x\text{cos}\frac{\pi }{8}\right)\left(2\text{cos}x\text{sin}\frac{\pi }{8}\right)=\left(2\text{sin}x\text{cos}x\right)\left(2\text{cos}\frac{\pi }{8}\text{sin}\frac{\pi }{8}\right)$

$=\text{sin}2x\text{sin}\frac{\pi }{4}=\frac{\sqrt{2}}{2}\text{sin}2x$

b) sin²y + 2cosxcosycos(x ‒ y) = cos²x + cos²(x ‒ y).

⇔ 2cosxcosycos(x ‒ y) ‒ cos²(x ‒ y) = cos²x ‒ sin²y

Ta có:

VT = 2cosxcosycos(x ‒ y) ‒ cos²(x ‒ y)

= cos(x – y)[2cosxcosy – cos(x – y)]

= cos(x – y)[2cosxcosy – (cosxcosy + sinxsiny)]

= cos(x – y)(cosxcosy – sinxsiny)

$=\text{cos}\left(x-y\right)\text{cos}\left(x+y\right)=\frac{1}{2}\left(\text{cos}2y+\text{cos}2x\right)$

$=\frac{1}{2}\left(1-2{\text{sin}}^{2}y+2{\text{cos}}^{2}x-1\right)={\text{cos}}^{2}x-{\text{sin}}^{2}y=VP.$

Vậy sin²y + 2cosxcosycos(x ‒ y) = cos²x + cos²(x ‒ y).

Bài 4 trang 34 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) $\cos \left(2x-\frac{\pi }{3}\right)+s\text{inx}=0;$

b) ${\cos }^2\left(x+\frac{\pi }{4}\right)=\frac{2+\sqrt{3}}{4};$

c) $\cos \left(3x+\frac{\pi }{6}\right)+2{\sin }^{2}x=1.$

Lời giải:

Bài 5 trang 34 SBT Toán 11 Tập 1: Vận tốc v₁ (cm/s) của con lắc đơn thứ nhất và vận tốc v₂ (cm/s) của con lắc đơn thứ hai theo thời gian t (giây) được cho bởi công thức:

$v_1\left(t\right)=-4\cos \left(\frac{2t}{3}+\frac{\pi }{4}\right)$ và $v_2\left(t\right)=2\sin \left(2t+\frac{\pi }{6}\right).$

Xác định các thời điểm t mà tại đó:

a) Vận tốc của con lắc đơn thứ nhất bằng 2 cm/s;

b) Vận tốc của con lắc đơn thứ nhất gấp hai lần vận tốc của con lắc đơn thứ hai.

Lời giải:

a) Thời điểm t mà tại đó vận tốc của con lắc đơn thứ nhất bằng 2 cm/s là nghiệm của phương trình:

$-4\cos \left(\frac{2t}{3}+\frac{\pi }{4}\right)=2$

$\iff \cos \left(\frac{2t}{3}+\frac{\pi }{4}\right)=-\frac{1}{2}$

$\iff \cos \left(\frac{2t}{3}+\frac{\pi }{4}\right)=\cos \frac{2\pi }{3}$

$\iff \frac{2t}{3}+\frac{\pi }{4}=\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$ hoặc $\frac{2t}{3}+\frac{\pi }{4}=-\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$

$\iff t=\frac{5\pi }{8}+k3\pi ,k\in \mathbb{Z}$ hoặc $t=-\frac{11\pi }{8}+k3\pi ,k\in \mathbb{Z}.$

b) Thời điểm t mà tại vận tốc của con lắc đơn thứ nhất gấp hai lần vận tốc của con lắc đơn thứ hai là nghiệm của phương trình:

Vậy thời điểm mà vận tốc của con lắc đơn thứ nhất gấp hai lần vận tốc của con lắc đơn thứ hai là $t=\frac{19\pi }{16}+k^{\text{'}}\frac{3\pi }{2},k^{\text{'}}\in \mathbb{Z}$ và $t=\frac{13\pi }{32}+k^{\text{'}}\frac{3\pi }{4},k^{\text{'}}\in \mathbb{Z}.$

Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Góc lượng giác

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài 5: Phương trình lượng giác cơ bản