Sách bài tập Toán 11 Bài 1 (Chân trời sáng tạo): Biến cố giao và quy tắc nhân xác suất

Giải SBT Toán 11 Bài 1: Biến cố giao và quy tắc nhân xác suất

Bài 1 trang 95 SBT Toán 11 Tập 2: Một hộp chứa 4 bút xanh, 1 bút đen và 1 bút đỏ. Các cây bút có cùng kích thước và khối lượng. Chọn ra ngẫu nhiên 3 cây bút từ hộp. Gọi A là biến cố “Có 1 cây bút đỏ trong 3 cây bút được lấy ra”. Gọi B là biến cố “Có 1 cây bút đen trong 3 cây bút được lấy ra”.

a) Hãy tìm một biến cố xung khắc với biến cố A nhưng không xung khắc với biến cố B.

b) Tính xác suất của các biến cố A, B và AB.

Lời giải:

a) Biến cố “Lấy ra được 1 bút đen và 2 bút xanh” xung khắc với biến cố A nhưng không xung khắc với biến cố B.

b) AB là biến cố “Lấy ra được 1 bút xanh, 1 bút đen và 1 bút đỏ”.

Không gian mẫu của phép thử là $n\left(\Omega \right)=C_6^3$.

Vì trong hộp có 1 cây bút đen và 1 cây bút đỏ nên xác suất của 2 biến cố A và B bằng nhau. Số trường hợp xảy ra của hai biến cố là $n\left(A\right)=n\left(B\right)=C_1^1{C}_5^2$.

Từ đó ta có:

$P\left(A\right)=P\left(B\right)=\frac{C_1^1{C}_5^2}{C_6^3}=\mathrm{0,5}$.

Số trường hợp xảy ra của biến cố AB là $n\left(AB\right)=C_4^1{C}_1^1{C}_1^1$. Từ đó ta có

$P\left(AB\right)=\frac{C_4^1{C}_1^1{C}_1^1}{C_6^3}=\mathrm{0,2}$.

Bài 2 trang 95 SBT Toán 11 Tập 2: Hộp thứ nhất chứa 4 viên bi xanh và 1 viên bi đỏ. Hộp thứ hai chứa 1 viên bi xanh và 3 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên từ mỗi hộp 2 viên bi. Gọi A là biến cố “Cả 2 viên bi lấy ra từ hộp thứ nhất có cùng màu”; B là biến cố “Cả 2 viên bi lấy ra từ hộp thứ hai có cùng màu”.

a) Minh nói AB là biến cố “Trong 4 viên bi lấy ra có 2 viên bi xanh, 2 viên bi đỏ”. Minh nói đúng hay sai? Tại sao?

b) So sánh P(AB) với P(A)P(B).

c) Hãy tìm một biến cố khác rỗng, xung khắc với cả biến cố A và biến cố B.

Lời giải:

a) Minh nói sai vì nếu lấy ra từ 2 hộp mỗi hộp 1 viên bi xanh, 1 viên bi đỏ thì trong 4 viên bi lấy ra có 2 viên bi xanh, 2 viên bi đỏ nhưng hai biến cố A và B đều không xảy ra.

b) Không gian mẫu của phép thử là $n\left(\Omega \right)=C_5^2{C}_4^2$.

Số trường hợp xảy ra của biến cố A là $n\left(A\right)=C_4^2{C}_4^2$.

Số trường hợp xảy ra của biến cố B là $n\left(B\right)=C_5^2{C}_3^2$.

Số trường hợp xảy ra của biến cố AB là $n\left(AB\right)=C_4^2{C}_3^2$.

Ta có

• $P\left(A\right)=\frac{C_4^2{C}_4^2}{C_5^2{C}_4^2}=\mathrm{0,6}$;

• $P\left(B\right)=\frac{C_5^2{C}_3^2}{C_5^2{C}_4^2}=\mathrm{0,5}$;

• $P\left(AB\right)=\frac{C_4^2{C}_3^2}{C_5^2{C}_4^2}=\mathrm{0,3}$.

Vậy $P\left(A\right)P\left(B\right)=P\left(AB\right)$.

c) Biến cố “Lấy ra từ mỗi hộp 1 viên bi xanh, 1 viên bi đỏ” xung khắc với cả hai biến cố A và B.

Bài 3 trang 96 SBT Toán 11 Tập 2: Một hộp chứa 50 tấm thẻ cùng loại được đánh số từ 1 đến 50. Chọn ra ngẫu nhiên 1 thẻ từ hộp. Gọi A là biến cố “Số ghi trên thẻ được chọn chia hết cho 4”, B là biến cố “Số ghi trên thẻ được chọn chia hết cho 6”.

a) Giang nói AB là biến cố “Số ghi trên thẻ được chọn chia hết cho 24”. Giang nói như vậy đúng hay sai? Tại sao?

b) Hai biến cố A và B có độc lập không? Tại sao?.

Lời giải:

a) Giang nói sai vì nếu lấy được thẻ ghi số 12 thì cả hai biến cố A và B đều xảy ra nhưng 12 không chia hết cho 24.

b) AB là biến cố “Số ghi trên thẻ được chọn chia hết cho 12”.

Không gian mẫu của phép thử là$n\left(\Omega \right)=50$.

Từ 1 đến 50 có 12 số chia hết cho 4 nên xác suất của biến cố A là

$P\left(A\right)=\frac{12}{50}$.

Từ 1 đến 50 có 8 số chia hết cho 6 nên xác suất của biến cố B là

$P\left(B\right)=\frac{8}{50}$.

Từ 1 đến 50 có 4 số chia hết cho 12 nên xác suất của biến cố AB là

$P\left(AB\right)=\frac{4}{50}$.

Vì $P\left(A\right)P\left(B\right)\ne P\left(AB\right)$ nên hai biến cố A và B không là hai biến cố độc lập.

Bài 4 trang 96 SBT Toán 11 Tập 2: Cho A và B là hai biến cố độc lập.

a) Biết $P\left(\overline{A}\right)=\mathrm{0,4}$ và P(B) = 0,1. Hãy tính xác suất của các biến cố AB, $\overline{A}B$ và $\overline{A}\overline{B}$.

b) Biết P(A) + P(B) = 0,8 và P(AB) = 0,16. Hãy tính xác suất của các biến cố B, $\overline{A}B$ và $\overline{A}\overline{B}$.

Lời giải:

Vì A và B là hai biến cố độc lập nên $\overline{A}$ và B; A và $\overline{B}$; $\overline{A}$ và $\overline{B}$ cũng độc lập.

a) Ta có

• $P\left(A\right)=1-P\left(\overline{A}\right)=1-\mathrm{0,4}=\mathrm{0,6}$;

• $P\left(\overline{B}\right)=1-P\left(B\right)=1-\mathrm{0,1}=\mathrm{0,9}$.

Do A và B; $\overline{A}$ và B; $\overline{A}$ và $\overline{B}$ độc lập nên

• $P\left(AB\right)=P\left(A\right)P\left(B\right)=\mathrm{0,6.0,1}=\mathrm{0,06}$;

• $P\left(\overline{A}B\right)=P\left(\overline{A}\right)P\left(B\right)=\mathrm{0,4.0,1}=\mathrm{0,04}$;

• $P\left(\overline{A}\overline{B}\right)=P\left(\overline{A}\right)P\left(\overline{B}\right)=\mathrm{0,4.0,9}=\mathrm{0,36}$.

b) Vì A và B là hai biến cố độc lập nên$P\left(A\right)P\left(B\right)=P\left(AB\right)=\mathrm{0,16}$.

Mà P(A) + P(B) = 0,8 nên $P\left(A\right)=P\left(B\right)=\mathrm{0,4}$.

• $P\left(\overline{A}\right)=1-P\left(A\right)=1-\mathrm{0,4}=\mathrm{0,6}$;

• $P\left(\overline{B}\right)=1-P\left(B\right)=1-\mathrm{0,4}=\mathrm{0,6}$.

Do $\overline{A}$ và B; $\overline{A}$ và $\overline{B}$ độc lập nên

• $P\left(\overline{A}B\right)=P\left(\overline{A}\right)P\left(B\right)=\mathrm{0,6.0,4}=\mathrm{0,24}$;

• $P\left(\overline{A}\overline{B}\right)=P\left(\overline{A}\right)P\left(\overline{B}\right)=\mathrm{0,6.0,6}=\mathrm{0,36}$.

Bài 5 trang 96 SBT Toán 11 Tập 2: Minh mua 2 bóng đèn. Theo một kết quả thống kê, tỉ lệ bị hỏng trong năm đầu sử dụng của loại bóng đèn Minh mua là 23%. Tính xác suất của các biến cố:

A: “Cả hai bóng đèn đều bị hỏng trong năm đầu sử dụng”;

B: “Cả hai bóng đèn đếu không bị hỏng trong năm đầu sử dụng”.

Lời giải:

Do tỉ lệ bóng bị hỏng trong năm đầu sử dụng là 23% nên xác suất 1 bóng bị hỏng trong năm đầu sử dụng là 0,23.

Xác suất để bóng không bị hỏng trong năm đầu sử dụng là 1 – 0,23 = 0,77.

Ta có

•P(A) = 0,23 . 0,23 = 0,0529;

•P(B) = 0,77 . 0,77 = 0,5929.

Vậy xác suất của biến cố A là 0,0529; xác suất của biến cố B là 0,5929.

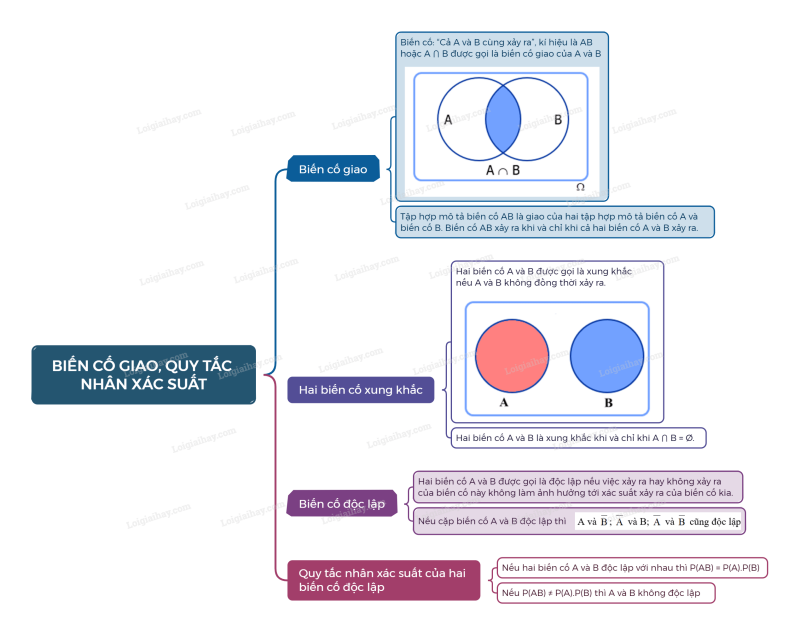
Lý thuyết Biến cố giao và quy tắc nhân xác suất

1. Biến cố giao

Cho hai biến cố A và B. Biến cố: “Cả A và B cùng xảy ra”, kí hiệu AB hoặc $A\cap B$ được gọi là biến cố giao của A và B.

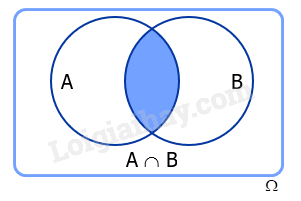
Chú ý: Tập hợp mô tả biến cố AB là giao của hai tập hợp mô tả biến cố A và biến cố B. Biến cố AB xảy ra khi và chỉ khi cả hai biến cố A và B xảy ra.

2. Hai biến cố xung khắc

Hai biến cố A và B được gọi là xung khắc nếu A và B không đồng thời xảy ra.

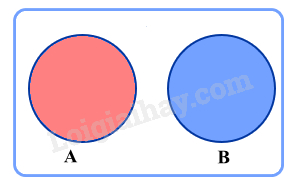
Chú ý: Hai biến cố A và B là xung khắc khi và chỉ khi $A\cap B=\mathrm{\varnothing }$.

3. Biến cố độc lập

Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng tới xác suất xảy ra của biến cố kia.

Nhận xét: Nếu hai biến cố A và B độc lập thì A và $\overline{B}$; $\overline{A}$ và B; $\overline{A}$ và $\overline{B}$ cũng độc lập.

4. Quy tắc nhân xác suất của hai biến cố độc lập

Nếu hai biến cố A và B độc lập với nhau thì $P\left(AB\right)=P\left(A\right).P\left(B\right)$.

Chú ý: Từ quy tắc nhân xác suất ta thấy, nếu $P\left(AB\right)\ne P\left(A\right)P\left(B\right)$ thì hai biến cố A và B không độc lập.

Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Khoảng cách trong không gian

Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài tập cuối chương 8

Bài 2: Biến cố hợp và quy tắc cộng xác suất

Bài tập cuối chương 9