Sách bài tập Toán 11 Bài 5 (Chân trời sáng tạo): Phương trình lượng giác cơ bản

Giải SBT Toán 11 Bài 5: Phương trình lượng giác cơ bản

Bài 1 trang 30 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) $\sin \left(3x+\frac{\pi }{6}\right)=\frac{\sqrt{3}}{2};$

b) cos(2x ‒ 30°) = ‒1;

c) 3sin(‒2x + 17°) = 4;

d) $\cos \left(3x-\frac{7\pi }{12}\right)=\cos \left(-x+\frac{\pi }{4}\right);$

e) $\sqrt{3}\tan \left(x-\frac{\pi }{4}\right)-1=0;$

g) $\cot \left(\frac{x}{3}+\frac{2\pi }{5}\right)=\cot \frac{\pi }{5}.$

Lời giải:

a) $\sin \left(3x+\frac{\pi }{6}\right)=\frac{\sqrt{3}}{2}$

$\iff \sin \left(3x+\frac{\pi }{6}\right)=\sin \left(\frac{\pi }{3}\right)$

$\iff 3x+\frac{\pi }{6}=\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$ hoặc $3x+\frac{\pi }{6}=\pi -\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{\pi }{18}+k\frac{2\pi }{3},k\in \mathbb{Z}$ hoặc $x=\frac{\pi }{6}+k\frac{2\pi }{3},k\in \mathbb{Z}$

Vậy phương trình có nghiệm là $x=\frac{\pi }{18}+k\frac{2\pi }{3},k\in \mathbb{Z}$ và $x=\frac{\pi }{6}+k\frac{2\pi }{3},k\in \mathbb{Z}$

b) cos(2x ‒ 30°) = ‒1

⇔ 2x ‒ 30° = 180° + k360° (k ∈ ℤ)

⇔ 2x = 210 + k360° (k ∈ ℤ)

⇔ x = 105° + k180° (k ∈ ℤ)

Vậy phương trình có nghiệm là x = 105° + k180° (k ∈ ℤ).

c) 3sin(‒2x + 17°) = 4

$\iff \sin \left(-2x+17°\right)=\frac{4}{3}$

Do $\frac{4}{3}>1$ nên phương trình vô nghiệm.

d) $\cos \left(3x-\frac{7\pi }{12}\right)=\cos \left(-x+\frac{\pi }{4}\right)$

$\iff 3x-\frac{7\pi }{12}=-x+\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}$
hoặc $3x-\frac{7\pi }{12}=-\left(-x+\frac{\pi }{4}\right)+k2\pi ,k\in \mathbb{Z}$

$\iff 4x=\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $2x=\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{5\pi }{24}+k\frac{\pi }{2},k\in \mathbb{Z}$ hoặc $x=\frac{\pi }{6}+k\pi ,k\in \mathbb{Z}$

Vậy phương trình có nghiệm là $x=\frac{5\pi }{24}+k\frac{\pi }{2},k\in \mathbb{Z}$ và $x=\frac{\pi }{6}+k\pi ,k\in \mathbb{Z}$

e) $\sqrt{3}\tan \left(x-\frac{\pi }{4}\right)-1=0$

$\iff \tan \left(x-\frac{\pi }{4}\right)=\frac{1}{\sqrt{3}}$

$\iff \tan \left(x-\frac{\pi }{4}\right)=\tan \frac{\pi }{6}$

$\iff x-\frac{\pi }{4}=\frac{\pi }{6}+k\pi ,k\in \mathbb{Z}$

$\iff x=\frac{5\pi }{12}+k\pi ,k\in \mathbb{Z}$

Vậy phương trình có nghiệm là $x=\frac{5\pi }{12}+k\pi ,k\in \mathbb{Z}$

g) $\cot \left(\frac{x}{3}+\frac{2\pi }{5}\right)=\cot \frac{\pi }{5}$

$\iff \frac{x}{3}+\frac{2\pi }{5}=\frac{\pi }{5}+k\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{3\pi }{5}+k3\pi ,k\in \mathbb{Z}$

Vậy phương trình có nghiệm là $x=-\frac{3\pi }{5}+k3\pi ,k\in \mathbb{Z}$

Bài 2 trang 31 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) cos(2x + 10°) = sin(50° ‒ x);

b) 8sin³x + 1 = 0;

c) (sinx + 3)(cotx ‒ 1) = 0;

d) tan(x ‒ 30°) ‒ cot50° = 0.

Lời giải:

a) cos(2x + 10°) = sin(50° ‒ x)

⇔ cos(2x + 10°) = cos(x + 40°)

⇔ 2x + 10° = x + 40°+ k360°, k ∈ ℤ hoặc 2x + 10° = ‒x ‒ 40°+ k360°, k ∈ ℤ

⇔ x = 30° + k360°, k ∈ ℤ hoặc $x=-\frac{1}{3}{.50}^{\circ }+k{120}^{\circ },k\in \mathbb{Z}$.

Vậy phương trình có các nghiệm là x = 30° + k360°, k ∈ ℤvà $x=-\frac{1}{3}\cdot {50}^{\circ }+k{120}^{\circ },k\in \mathbb{Z}.$

b) 8sin³x + 1 = 0

$\iff {\sin }^{3}x=-\frac{1}{8}\iff \sin x=-\frac{1}{2}$

$\iff x=-\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $x=\pi -\left(-\frac{\pi }{6}\right)+k2\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $x=\frac{7\pi }{6}+k2\pi ,k\in \mathbb{Z}$

Vậy phương trình có các nghiệm là $x=-\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ và $x=\frac{7\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

c) (sinx + 3)(cotx ‒ 1) = 0

⇔ sinx + 3 = 0 hoặc cotx ‒ 1 = 0

⇔ sinx = ‒3 hoặc cotx = 1

Phương trình sinx = ‒3 vô nghiệm.

Phương trình cotx = 1 có nghiệm là $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$.

Vậy phương trình có các nghiệm là $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$.

d) tan(x ‒ 30°) ‒ cot50° = 0

⇔ tan(x ‒ 30°) = cot50°

⇔ tan(x ‒ 30°) = tan40°

⇔ x ‒ 30° = 40° + k180°, k ∈ ℤ

⇔ x = 70° + k180°, k ∈ ℤ

Vậy phương trình có các nghiệm là x = 70° + k180°, k ∈ ℤ.

Bài 3 trang 31 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) $\cos \left(x+\frac{\pi }{4}\right)+\cos \left(\frac{\pi }{4}-x\right)=0;$

b) 2cos²x + 5sinx ‒ 4 = 0;

c) $\cos \left(3x-\frac{\pi }{4}\right)+2{\sin }^{2}x-1=0.$

Lời giải:

a) $\text{cos}\left(x+\frac{\pi }{4}\right)+\text{cos}\left(\frac{\pi }{4}-x\right)=0$

$\iff \text{cos}\left(x+\frac{\pi }{4}\right)=-\text{cos}\left(\frac{\pi }{4}-x\right)\iff \text{cos}\left(x+\frac{\pi }{4}\right)=\text{cos}\left(\frac{3\pi }{4}+x\right)$

$\iff x+\frac{\pi }{4}=\frac{3\pi }{4}+x+k2\pi ,k\in \mathbb{Z}$ hoặc $x+\frac{\pi }{4}=-\frac{3\pi }{4}-x+k2\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$

Vậy phương trình có các nghiệm là $x=-\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$

b) 2cos²x + 5sinx ‒ 4 = 0

⇔ 2(1 ‒ sin²x) + 5sinx ‒ 4 = 0

⇔ ‒2sin²x + 5sinx ‒ 2 = 0

⇔ sinx = 2 (vô nghiệm) hoặc sinx = $\frac{1}{2}$

⇔ sinx = $\frac{1}{2}$ $\iff x=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $x=\pi -\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $x=\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$

Vậy phương trình có các nghiệm $x=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ và $x=\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$

c) $\text{cos}\left(3x-\frac{\pi }{4}\right)+2{\text{sin}}^{2}x-1=0$

$\iff \text{cos}\left(3x-\frac{\pi }{4}\right)=1-2{\text{sin}}^{2}x\iff \text{cos}\left(3x-\frac{\pi }{4}\right)=\text{cos}2x$

$\iff 3x-\frac{\pi }{4}=2x+k2\pi ,k\in \mathbb{Z}$ hoặc $3x-\frac{\pi }{4}=-2x+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}$ hoặc $x=\frac{\pi }{20}+k\frac{2\pi }{5},k\in \mathbb{Z}$

Vậy phương trình có các nghiệm là $x=\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}$ và $x=\frac{\pi }{20}+k\frac{2\pi }{5},k\in \mathbb{Z}$

Bài 4 trang 31 SBT Toán 11 Tập 1: Tìm tập xác định của hàm số lượng giác $y=\frac{s\text{inx}-2\cos 3x}{s\text{inx}+\sin \left(2x-\frac{\pi }{3}\right)}.$

Lời giải:

Hàm số xác định khi và chỉ khi $\text{sin}x+\text{sin}\left(2x-\frac{\pi }{3}\right)\ne 0.$

Ta có $\text{sin}x+\text{sin}\left(2x-\frac{\pi }{3}\right)=0$

$\iff \text{sin}x=-\text{sin}\left(2x-\frac{\pi }{3}\right)$

$\iff \text{sin}x=\text{sin}\left(-2x+\frac{\pi }{3}\right)$

$\iff x=-2x+\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$ hoặc $x=\pi +2x-\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$

$\iff 3x=\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$ hoặc $x=-\frac{2\pi }{3}-k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{\pi }{9}+k\frac{2\pi }{3},k\in \mathbb{Z}$ hoặc $x=-\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$

(do $x=-\frac{2\pi }{3}-k2\pi ,k\in \mathbb{Z}$ và $x=-\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$ có cùng điểm biểu diễn trên đường tròn lượng giác.)

Do đó $\text{sin}x+\text{sin}\left(2x-\frac{\pi }{3}\right)\ne 0$ khi và chỉ khi $x\ne \frac{\pi }{9}+k\frac{2\pi }{3},k\in \mathbb{Z}$ và $x\ne -\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}.$

Bài 5 trang 31 SBT Toán 11 Tập 1: Tìm các nghiệm của mỗi phương trình sau trong khoảng (‒π; π).

a) $\sin \left(3x-\frac{\pi }{3}\right)=1;$

b) $2\cos \left(2x-\frac{3\pi }{4}\right)=\sqrt{3};$

c) $\tan \left(x+\frac{\pi }{9}\right)=\tan \frac{4\pi }{9}.$

Lời giải:

a) $\sin \left(3x-\frac{\pi }{3}\right)=1$

$\iff 3x-\frac{\pi }{3}=\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}$

$\iff 3x=\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{5\pi }{18}+k\frac{2\pi }{3},k\in \mathbb{Z}$

Lại có x ∈ (‒π; π) nên ta có:

$-\pi <\frac{5\pi }{18}+k\frac{2\pi }{3}<\pi$ $\iff -1<\frac{5}{18}+k\frac{2}{3}<1$ $\iff -\frac{23}{12}<k<\frac{13}{12}$

Mà k ∈ ℤ nên k ∈ {–1; 0; 1}.

Với k = ‒1, ta có: $x=\frac{5\pi }{18}-1\cdot \frac{2\pi }{3}=-\frac{7\pi }{18}$

Với k = 0, ta có: $x=\frac{5\pi }{18}+0\cdot \frac{2\pi }{3}=\frac{5\pi }{18}$

Với k = 1, ta có: $x=\frac{5\pi }{18}+1\cdot \frac{2\pi }{3}=\frac{17\pi }{18}$

Vậy phương trình có nghiệm $x\in \left\{-\frac{7\pi }{18};\frac{5\pi }{18};\frac{17\pi }{18}\right\}.$

b) $2\cos \left(2x-\frac{3\pi }{4}\right)=\sqrt{3}$

$\iff \cos \left(2x-\frac{3\pi }{4}\right)=\frac{\sqrt{3}}{2}$

$\iff \cos \left(2x-\frac{3\pi }{4}\right)=\cos \frac{\pi }{6}$

$\iff 2x-\frac{3\pi }{4}=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $2x-\frac{3\pi }{4}=-\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$

$\iff 2x=\frac{11\pi }{12}+k2\pi ,k\in \mathbb{Z}$ hoặc $2x=\frac{7\pi }{12}+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{11\pi }{24}+k\pi ,k\in \mathbb{Z}$ hoặc $x=\frac{7\pi }{24}+k\pi ,k\in \mathbb{Z}$

Lại có x ∈ (‒π; π) nên ta có:

⦁ $-\pi <\frac{11\pi }{24}+k\pi <\pi$ $\iff -1<\frac{11}{24}+k<1$ $\iff -\frac{35}{24}<k<\frac{13}{24}$

Mà k ∈ ℤ nên k ∈ {–1; 0}.

⦁ $-\pi <\frac{7\pi }{24}+k\pi <\pi$ $\iff -1<\frac{7}{24}+k<1$ $\iff -\frac{31}{24}<k<\frac{17}{24}$

Mà k ∈ ℤ nên k ∈ {–1; 0}.

Với k = ‒1, ta có $x=\frac{11\pi }{24}+\left(-1\right)\cdot \pi =-\frac{13\pi }{24}$ hoặc $x=\frac{7\pi }{24}+\left(-1\right)\cdot \pi =\frac{-17\pi }{24}$

Với k = 0, ta có $x=\frac{11\pi }{24}+0\cdot \pi =\frac{11\pi }{24}$ hoặc $x=\frac{7\pi }{24}+0\cdot \pi =\frac{7\pi }{24}$

Vậy phương trình có nghiệm $x\in \left\{-\frac{17\pi }{24};-\frac{13\pi }{24};\frac{7\pi }{24};\frac{11\pi }{24}\right\}.$

c) $\tan \left(x+\frac{\pi }{9}\right)=\tan \frac{4\pi }{9}$

$\iff x+\frac{\pi }{9}=\frac{4\pi }{9}+k\pi ,k\in \mathbb{Z}$

$\iff x=\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}$

Lại có x ∈ (‒π; π) nên ta có:

$-\pi <\frac{\pi }{3}+k\pi <\pi$ $\iff -1<\frac{1}{3}+k<1$ $\iff -\frac{4}{3}<k<\frac{2}{3}$

Mà k ∈ ℤ nên k ∈ {–1; 0}.

Với k = −1, ta có: $x=\frac{\pi }{3}+\left(-1\right)\cdot \pi =-\frac{2\pi }{3};$

Với k = 0, ta có: $x=\frac{\pi }{3}+0\cdot \pi =\frac{\pi }{3}$

Vậy phương trình có nghiệm $x\in \left\{-\frac{2\pi }{3};\frac{\pi }{3}\right\}.$

Bài 6 trang 31 SBT Toán 11 Tập 1: Tìm hoành độ các giao điểm của đồ thị các hàm số sau:

a) $y=\sin \left(2x-\frac{\pi }{3}\right)$ và $y=\sin \left(\frac{\pi }{4}-x\right);$

b) $y=\cos \left(3x-\frac{\pi }{4}\right)$ và $y=\cos \left(x+\frac{\pi }{6}\right).$

Lời giải:

a) Hoành độ các giao điểm của đồ thị 2 hàm số là nghiệm của phương trình: $\sin \left(2x-\frac{\pi }{3}\right)=\sin \left(\frac{\pi }{4}-x\right)$

$\iff 2x-\frac{\pi }{3}=\frac{\pi }{4}-x+k2\pi ,k\in \mathbb{Z}$ hoặc $2x-\frac{\pi }{3}=\pi -\left(\frac{\pi }{4}-x\right)+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{7\pi }{36}+k\frac{2\pi }{3},k\in \mathbb{Z}$hoặc $x=\frac{13\pi }{12}+k2\pi ,k\in \mathbb{Z}$

Vậy hoành độ các giao điểm của đồ thị 2 hàm số là: $x=\frac{7\pi }{36}+k\frac{2\pi }{3},k\in \mathbb{Z}$ và $x=\frac{13\pi }{12}+k2\pi ,k\in \mathbb{Z}$

b) Hoành độ các giao điểm của đồ thị 2 hàm số là nghiệm của phương trình:

$\cos \left(3x-\frac{\pi }{4}\right)=\cos \left(x+\frac{\pi }{6}\right)$

$\iff 3x-\frac{\pi }{4}=x+\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $3x-\frac{\pi }{4}=-\left(x+\frac{\pi }{6}\right)+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{5\pi }{24}+k\pi ,k\in \mathbb{Z}$ hoặc $x=\frac{\pi }{48}+k\frac{\pi }{2},k\in \mathbb{Z}$

Vậy hoành độ các giao điểm của đồ thị 2 hàm số là: $x=\frac{5\pi }{24}+k\pi ,k\in \mathbb{Z}$ và $x=\frac{\pi }{48}+k\frac{\pi }{2},k\in \mathbb{Z}$.

Bài 7 trang 31 SBT Toán 11 Tập 1: Tìm hoành độ các giao điểm của đồ thị hàm số $y=\sin 3x-\cos \left(\frac{3\pi }{4}-x\right)$ với trục hoành.

Lời giải:

Hoành độ các giao điểm của đồ thị hàm số $y=\sin 3x-\cos \left(\frac{3\pi }{4}-x\right)$ với trục hoành là nghiệm của phương trình:

$\sin 3x-\cos \left(\frac{3\pi }{4}-x\right)=0$

$\iff \sin 3x=\cos \left(\frac{3\pi }{4}-x\right)$

$\iff \sin 3x=\sin \left[\frac{\pi }{2}-\left(\frac{3\pi }{4}-x\right)\right]$

$\iff \sin 3x=\sin \left(x-\frac{\pi }{4}\right)$

$\iff 3x=x-\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}$ hoặc $3x=\pi -\left(x-\frac{\pi }{4}\right)+k2\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{\pi }{8}+k\pi ,k\in \mathbb{Z}$ và $x=\frac{5\pi }{16}+k\frac{\pi }{2},k\in \mathbb{Z}$.

Vậy hoành độ các giao điểm của đồ thị hàm số $y=\sin 3x-\cos \left(\frac{3\pi }{4}-x\right)$ với trục hoành là $x=-\frac{\pi }{8}+k\pi ,k\in \mathbb{Z}$ và $x=\frac{5\pi }{16}+k\frac{\pi }{2},k\in \mathbb{Z}$.

Bài 8 trang 31 SBT Toán 11 Tập 1: Theo Định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số $\frac{\sin i}{s\text{in r}},$ với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là 45° thì góc khúc xạ bằng 30°. Khi góc tới là 60° thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.

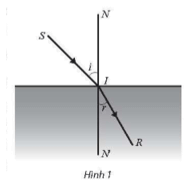
Lời giải:

Vì tỉ số $\frac{\sin i}{\text{sin r}}$ là một hằng số phụ thuộc vào chiết suất của hai môi trường nên ta có:

$\frac{\text{sin}45°}{\text{sin}30°}=\frac{\text{sin}60°}{\text{sin}r}$ nên $\text{sin}r=\frac{\text{sin}60°\text{sin}30°}{\text{sin}45°}=\frac{\sqrt{6}}{4}$. Suy ra r ≈ 37,76°.

Bài 9 trang 32 SBT Toán 11 Tập 1: Một quả bóng được ném xiên một góc α (0° ≤ α ≤ 90°) từ mặt đất với tốc độ v₀ (m/s). Khoảng cách theo phương ngang từ vị trí ban đầu của quả bóng đến vị trí bóng chạm đất được tính bởi công thức $d=\frac{v_0^2\sin 2\alpha }{10}.$

a) Tính khoảng cách d khi bóng được ném đi với tốc độ ban đầu 10 m/s và góc ném là 30° so với phương ngang.

b) Nếu tốc độ ban đầu của bóng là 10 m/s thì cần ném bóng với góc bao nhiêu độ để khoảng cách d là 5 m?

Lời giải:

a) Khoảng cách d khi bóng được ném đi với tốc độ ban đầu 10 m/s và góc ném là 30° so với phương ngang là:

d = $\frac{{10}^2\cdot \sin \left(2\cdot 30°\right)}{10}=5\sqrt{3}\approx 8,66$ (m)

b) Từ d = $\frac{v_0^2\sin 2\alpha }{10}$ suy ra $\sin 2\alpha =\frac{10d}{v_0^2}$

Để khoảng cách d là 5 m thì ta có $\sin 2\alpha =\frac{10d}{v_0^2}=\frac{10\cdot 5}{{10}^2}=\frac{1}{2}$

⇔ 2α = 30° hoặc 2α = 150° (do 0° ≤ α ≤ 90°)

⇔ α = 15° hoặc α = 75°.

Vậy cần ném bóng với góc 15° hoặc 75° để khoảng cách d là 5 m.

Bài 10 trang 32 SBT Toán 11 Tập 1: Chiều cao h(m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức $h\left(t\right)=30+20\sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right).$

a) Cabin đạt độ cao tối đa là bao nhiêu?

b) Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên?

Lời giải:

a) Với mọi t > 0, ta có $-1\le \sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right)\le 1$

$\iff -20\le 20\sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right)\le 20$

$\iff 10\le 30+20\sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right)\le 50$

Hay 10 ≤ h(t) ≤ 50

Vậy cabin đạt độ cao tối đa là 50 (m).

b) Thời gian để cabin đạt độ cao 40 m lần đầu tiên là nghiệm của phương trình:

$30+20\sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right)=40$ với t > 0 và t đạt giá trị nhỏ nhất.

Giải phương trình:

30 + $20\sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right)$ = 40

$\iff \sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right)=\frac{1}{2}$

$\iff \sin \left(\frac{\pi }{25}t+\frac{\pi }{3}\right)=\sin \frac{\pi }{6}$

$\iff \frac{\pi }{25}t+\frac{\pi }{3}=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ hoặc $\frac{\pi }{25}t+\frac{\pi }{3}=\pi -\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$

$\iff t=-\frac{25}{6}+k50,k\in \mathbb{Z}$ hoặc $t=\frac{25}{2}+k50,k\in \mathbb{Z}$

⦁ Xét $t=-\frac{25}{6}+k50,k\in \mathbb{Z}$ và t > 0, ta có:

$-\frac{25}{6}+k50>0\iff k>\frac{1}{12}$, k ∈ ℤ nên k ∈ {1; 2; …}

Mà t đạt giá trị nhỏ nhất nên $t=-\frac{25}{6}+1\cdot 50=\frac{275}{6}\approx 45,8\left(s\right)$ với k = 1.

⦁ Xét $t=\frac{25}{2}+k50,k\in \mathbb{Z}$ và t > 0, ta có:

$t=\frac{25}{2}+k50>0\iff k>-\frac{1}{4}$, k ∈ ℤ nên k ∈ {0; 1; 2; …}

Mà t đạt giá trị nhỏ nhất nên $t=\frac{25}{2}+0\cdot 50=\frac{25}{2}=12,5\left(s\right)$ với k = 0.

Do 12,5 < 45,8 nên sau 12,5 giây thì cabin đạt độ cao 40 m lần đầu tiên.

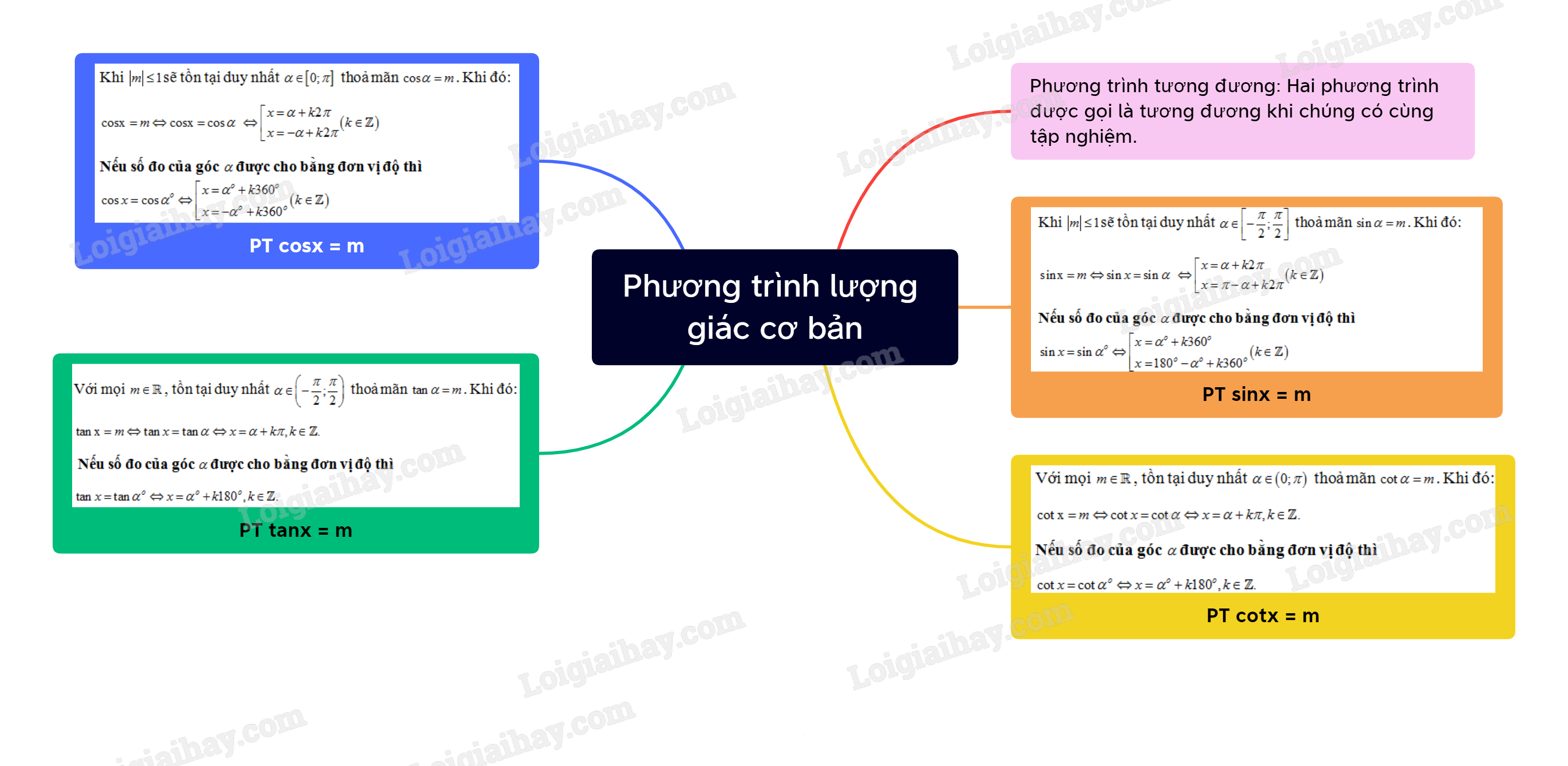
Lý thuyết Phương trình lượng giác cơ bản

1. Phương trình tương đương

- Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.

- Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết $f(x)=0\iff g(x)=0$

- Các phép biến đổi tương đương:

+ Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức.

+ Nhân hoặc chia 2 vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.

2. Phương trình $\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x}=m$

Phương trình sinx = m ,

• Nếu $\left|m\right|\le 1$ thì phương trình vô nghiệm.
• Nếu $\left|m\right|\le 1$ thì phương trình có nghiệm:

Khi đó, tồn tại duy nhất $\alpha \in \left[-\frac{\pi }{2};\frac{\pi }{2}\right]$ thoả mãn $\sin \alpha =m$,

$\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x}=m\iff \sin x=\sin \alpha$ $\iff [\begin{array}{l}x=\alpha +k2\pi \\ x=\pi -\alpha +k2\pi \end{array}\left(k\in \mathbb{Z}\right)$

* Chú ý:

a, Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì $\sin x=\sin {\alpha }^o\iff [\begin{array}{l}x={\alpha }^o+k{360}^o\\ x={180}^o-{\alpha }^o+k{360}^o\end{array}\left(k\in \mathbb{Z}\right)$

b, Một số trường hợp đặc biệt

$\begin{array}{l}\sin x=0\iff x=k\pi ,k\in \mathbb{Z}.\\ \sin x=1\iff x=\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}.\\ \sin x=-1\iff x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}.\end{array}$

3. Phương trình $\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m$

Phương trình $\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m$,

• Nếu $\left|m\right|\le 1$ thì phương trình vô nghiệm.
• Nếu $\left|m\right|\le 1$ thì phương trình có nghiệm:

Khi $\left|m\right|\le 1$sẽ tồn tại duy nhất $\alpha \in \left[0;\pi \right]$ thoả mãn $\mathrm{c}\mathrm{o}\mathrm{s}\alpha =m$. Khi đó:

$\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m\iff \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=\mathrm{c}\mathrm{o}\mathrm{s}\alpha$ $\iff [\begin{array}{l}x=\alpha +k2\pi \\ x=-\alpha +k2\pi \end{array}\left(k\in \mathbb{Z}\right)$

* Chú ý:

a, Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì $\cos x=\cos {\alpha }^o\iff [\begin{array}{l}x={\alpha }^o+k{360}^o\\ x=-{\alpha }^o+k{360}^o\end{array}\left(k\in \mathbb{Z}\right)$

b, Một số trường hợp đặc biệt

$\begin{array}{l}\mathrm{c}\mathrm{o}\mathrm{s}x=0\iff x=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}.\\ \mathrm{c}\mathrm{o}\mathrm{s}x=1\iff x=k2\pi ,k\in \mathbb{Z}.\\ \mathrm{c}\mathrm{o}\mathrm{s}x=-1\iff x=\pi +k2\pi ,k\in \mathbb{Z}.\end{array}$

4. Phương trình $\tan x=m$

Phương trình $\tan x=m$ có nghiệm với mọi m.

Với mọi $m\in \mathbb{R}$, tồn tại duy nhất $\alpha \in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ thoả mãn $\tan \alpha =m$. Khi đó:

$\tan \mathrm{x}=m\iff \tan x=\tan \alpha \iff x=\alpha +k\pi ,k\in \mathbb{Z}.$

*Chú ý: Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì

$\tan x=\tan {\alpha }^o\iff x={\alpha }^o+k{180}^o,k\in \mathbb{Z}.$

5. Phương trình $\cot x=m$

Phương trình $\cot x=m$ có nghiệm với mọi m.

Với mọi $m\in \mathbb{R}$, tồn tại duy nhất $\alpha \in \left(0;\pi \right)$ thoả mãn $\cot \alpha =m$. Khi đó:

$\cot \mathrm{x}=m\iff \cot x=\cot \alpha \iff x=\alpha +k\pi ,k\in \mathbb{Z}.$

*Chú ý: Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì

$\cot x=\cot {\alpha }^o\iff x={\alpha }^o+k{180}^o,k\in \mathbb{Z}.$

6. Giải phương trình lượng giác bằng máy tính cầm tay

Bước 1. Chọn đơn vị đo góc (độ hoặc radian).

Muốn tìm số đo độ, ta ấn: SHIFT $\to$MODE $\to$3 (CASIO FX570VN).

Muốn tìm số đo radian, ta ấn: SHIFT $\to$MODE $\to$4 (CASIO FX570VN).

Bước 2. Tìm số đo góc.

Khi biết SIN, COS, TANG của góc $\alpha$ta cần tìm bằng m, ta lần lượt ấn các phím SHIFT và một trong các phím SIN, COS, TANG rồi nhập giá trị lượng giác m và cuối cùng ấn phím “BẰNG =”. Lúc này trên màn hình cho kết quả là số đo của góc $\alpha$.

Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Góc lượng giác

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài tập cuối chương 1 trang 32