Sách bài tập Toán 11 Bài 1 (Chân trời sáng tạo): Góc lượng giác

Giải SBT Toán 11 Bài 1: Góc lượng giác

Bài 1 trang 8 SBT Toán 11 Tập 1: Đổi số đo của các góc sau đây sang radian:

a) 15°; b) 65°; c) ‒105°; d) ${\left(\frac{-5}{\pi }\right)}^{°}$

Lời giải:

a) $15°=\frac{15\pi }{180}=\frac{\pi }{12};$

b) $65°=\frac{65\pi }{180}=\frac{13\pi }{36};$

c) $-105°=-\frac{105\pi }{180}=-\frac{7\pi }{12};$

d) ${\left(-\frac{5}{\pi }\right)}^o=\frac{\left(-\frac{5}{\pi }\right)\pi }{180}=-\frac{5}{180}=-\frac{1}{36}.$

Bài 2 trang 8 SBT Toán 11 Tập 1: Đổi số đo của các góc sau đây sang độ:

a) 6; b) $\frac{4\pi }{15};$ c) $\frac{-19\pi }{8};$ d) $\frac{5}{3}.$

Lời giải:

a) $6rad={\left(6\cdot \frac{180}{\pi }\right)}^{°}=\mathrm{343,77}°.$

b) $\frac{4\pi }{15}rad={\left(\frac{4\pi }{15}\cdot \frac{180}{\pi }\right)}^{°}=48°.$

c) $-\frac{19\pi }{8}={\left(-\frac{19\pi }{8}\cdot \frac{180}{\pi }\right)}^{°}=-\mathrm{427,5}°.$

d) $\frac{5}{3}rad={\left(\frac{5}{3}\cdot \frac{180}{\pi }\right)}^{°}=\mathrm{95,49}°.$

Bài 3 trang 8 SBT Toán 11 Tập 1: Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây. Biết trong các Hình 4a, b, c có $\widehat{AOB}=\frac{\pi }{4};$ trong các hình 4d, e, g có $\widehat{CID}=82°.$

Lời giải:

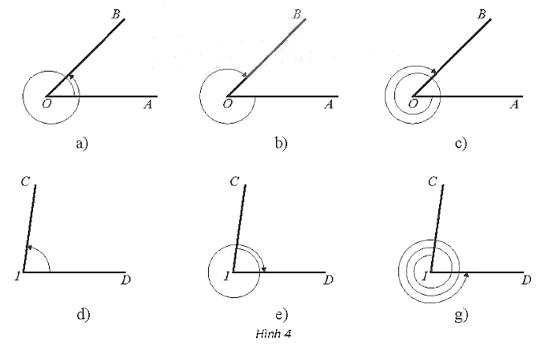
a) Số đo góc lượng giác (OA, OB) trong Hình 4a là: $\frac{\pi }{4}+2\pi =\frac{9\pi }{4}.$

b) Số đo góc lượng giác (OA, OB) trong Hình 4b là: $\frac{\pi }{4}-2\pi =-\frac{7\pi }{4}.$

c) Số đo góc lượng giác (OA, OB) trong Hình 4c là: $\frac{\pi }{4}-2\cdot 2\pi =-\frac{15\pi }{4}.$

d) Số đo góc lượng giác (IC, ID) trong Hình 4d là: 82°.

e) Số đo góc lượng giác (IC, ID) trong Hình 4e là: ‒82° ‒ 360° = ‒442°.

g) Số đo góc lượng giác (IC, ID) trong Hình 4g là: ‒82 + 360°.3 = 998°.

Bài 4 trang 9 SBT Toán 11 Tập 1: Hãy tìm số đo α của góc lượng giác (Om, On), với ‒π ≤ α < π, biết một góc lượng giác cùng tia đầu Om và tia cuối On có số đo là:

a) $\frac{36\pi }{5};$ b) $\frac{-75\pi }{14};$ c) $\frac{39\pi }{8};$ d) 2023π.

Lời giải:

a) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là $\alpha =\frac{36\pi }{5}+k2\pi \left(k\in \mathbb{Z}\right)$

Ta có ‒π ≤ α < π, suy ra $-\pi \le \frac{36\pi }{5}+k2\pi <\pi$

Do đó $-\frac{41\pi }{5}\le k2\pi <-\frac{31\pi }{5}$, suy ra $-\frac{41}{10}\le k<-\frac{31}{10}$.

Vì k ∈ ℤ nên k = ‒4.

Vậy $\alpha =\frac{36\pi }{5}+\left(-4\right).2\pi =\frac{-4\pi }{5}.$

b) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là $\alpha =-\frac{75\pi }{14}+k2\pi \left(k\in \mathbb{Z}\right)$

Ta có ‒π ≤ α < π, suy ra $-\pi +\frac{75\pi }{14}\le k2\pi <\pi +\frac{75\pi }{14}$, suy ra $\frac{61}{28}\le k<\frac{89}{28}$.

Vì k ∈ ℤ nên k = 3.

Vậy $\alpha =-\frac{75\pi }{14}+3.2\pi =\frac{9\pi }{14}.$

c) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là $\alpha =\frac{39\pi }{8}+k2\pi \left(k\in \mathbb{Z}\right)$.

Ta có ‒π ≤ α < π, suy ra $-\pi \le \frac{39\pi }{8}+k2\pi <\pi$

Do đó $-\pi -\frac{39\pi }{8}\le k2\pi <\pi -\frac{39\pi }{8}$, suy ra $-\frac{47}{16}\le k<-\frac{31}{16}$.

Vì k ∈ ℤ nên k = ‒2.

Vậy $\alpha =\frac{39\pi }{8}+\left(-2\right).2\pi =\frac{7\pi }{8}.$

d) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là α = 2023π + k2π (k ∈ ℤ).

Ta có ‒π ≤ α < π, suy ra ‒2024π ≤ k2π < ‒2022π, suy ra ‒1012 ≤ k < ‒1011.

Vì k ∈ ℤ nên k = ‒1012.

Vậy α = 2023π + (‒1012).2π = ‒π.

Bài 5 trang 9 SBT Toán 11 Tập 1: Cho một góc lượng giác có số đo là 375°.

a) Tìm số lớn nhất trong các số đo của góc lượng giác cùng tia đầu, tia cuối với góc đó mà có số đo âm;

b) Tìm số nhỏ nhất trong các số đo của góc lượng giác cùng tia đầu, tia cuối với góc đó mà có số đo dương.

Lời giải:

Góc lượng giác cùng tia đầu, tia cuối với góc có số đo là 375° là 375° + k360° (k ∈ ℤ).

a) Góc này có số đo âm nên 375° + k360° < 0°, do đó $k<\frac{-375}{360}=\frac{-25}{24}$

Mà k ∈ ℤ và góc này có số đo âm lớn nhất nên k = −2

Khi đó góc cần tìm có số đo là 375° + (−2).360° = -345°.

b) Góc này có số đo dương nên 375° + k360° > 0°, do đó $k>\frac{-375}{360}=\frac{-25}{24}$

Mà k ∈ ℤ và góc này có số đo dương nhỏ nhất nên k = −1

Khi đó góc cần tìm có số đo là 375° + (−1).360° = 15°.

Bài 6 trang 9 SBT Toán 11 Tập 1: Viết công thức tổng quát của số đo góc lượng giác (Om, On) dưới dạng a° + k360° (k ∈ ℤ), với 0 ≤ a < 360, biết một góc lượng giác với tia đầu Om, tia cuối On có số đo:

a) 1935°; b) ‒450°; c) ‒1440°; d) 754,5°.

Lời giải:

a) Ta có 1935° = 135° + 5.360° nên công thức tổng quát của số đo góc lượng giác (Om, On) là (Om, On) = 135° + k360° (k ∈ ℤ).

b) Ta có ‒450° = 270° ‒ 2.360° nên công thức tổng quát của số đo góc lượng giác (Om, On) là (Om, On) = 270° +k360° (k ∈ ℤ).

c) Ta có ‒1440° = ‒4.360° nên công thức tổng quát của số đo góc lượng giác (Om, On) là (Om, On) =k360° (k ∈ ℤ).

d) Ta có 754,5° = 34,5° + 2.360° nên công thức tổng quát của số đo góc lượng giác (Om, On) là (Om, On) = 34,5° +k360° (k ∈ ℤ).

Bài 7 trang 9 SBT Toán 11 Tập 1: Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:

a) ‒1965°; b) $\frac{48\pi }{5}.$

Lời giải:

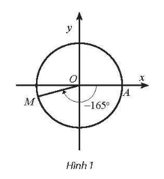
a) Ta có ‒1965° = ‒165° + (‒5).360°. Vậy điểm biểu diễn góc lượng giác có số đo ‒1965° là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ III sao cho $\widehat{AOM}=165°$ như Hình 1.

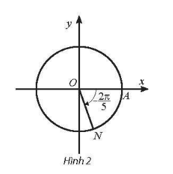
b) Ta có $\frac{48\pi }{5}=-\frac{2\pi }{5}+10\pi$. Vậy điểm biểu diễn góc lượng giác có số đo $\frac{48\pi }{5}$ là điểm N trên đường tròn lượng giác thuộc góc phần tư thứ IV sao cho $\widehat{AON}=\frac{2\pi }{5}$ như Hình 2.

Bài 8 trang 9 SBT Toán 11 Tập 1:

a) Góc lượng giác ‒245° có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?

‒605°; ‒65°; 115°; 205°; 475°.

b) Góc lượng giác $\frac{24\pi }{5}$ có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?

$\frac{-16\pi }{5};\frac{-\pi }{5};\frac{14\pi }{5};\frac{29\pi }{5};\frac{53\pi }{10}.$

Lời giải:

a) Hiệu số đo của góc lượng giác ‒245° với góc lượng giác ‒605°; ‒65°; 115°; 205°; 475° là:

‒245° ‒ (‒605°) = 360°;

‒245°‒ (‒65°) = ‒180°;

‒245° ‒ 115° = ‒360°;

‒245° ‒ 205° = ‒450°;

‒245° ‒ 475° = ‒720° = - 2.360°.

Vậy góc lượng giác ‒245° có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác là: ‒605°; 115°; 475°

b) Hiệu số đo của góc lượng giác $\frac{24\pi }{5}$ với góc lượng giác $\frac{-16\pi }{5};\frac{-\pi }{5};\frac{14\pi }{5};\frac{29\pi }{5};\frac{53\pi }{10}.$ là:

$\frac{24\pi }{5}-\left(-\frac{16\pi }{5}\right)=\frac{24\pi }{5}+\frac{16\pi }{5}=8\pi =4.2\pi ;$

$\frac{24\pi }{5}-\left(-\frac{\pi }{5}\right)=\frac{24\pi }{5}+\frac{\pi }{5}=5\pi =2.2\pi +\pi ;$

$\frac{24\pi }{5}-\frac{14\pi }{5}=2\pi ;$

$\frac{24\pi }{5}-\left(\frac{29\pi }{5}\right)=-\pi ;$

$\frac{24\pi }{5}-\frac{53\pi }{10}=\frac{48\pi }{10}-\frac{53\pi }{10}=-\frac{\pi }{2}.$

Vậy góc lượng giác $\frac{24\pi }{5}$ có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác là: $-\frac{16\pi }{5};\frac{14\pi }{5}.$

Bài 9 trang 9 SBT Toán 11 Tập 1: Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng là:

a) $\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right);$ b) $\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right);$

Lời giải:

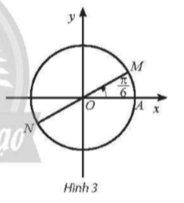
a) Trên đường tròn lượng giác, các góc có số đo $\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi hai điểm M và N như Hình 3.

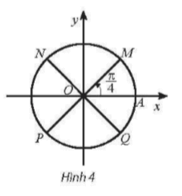
b) Trên đường tròn lượng giác, các góc có số đo $\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ được biễu diễn bởi bốn điểm M, N, P, Q như Hình 4.

Bài 10 trang 9 SBT Toán 11 Tập 1: Trong hình bên, các điểm M, A’, N tạo thành ba đỉnh của một tam giác đều. Vị trí các điểm M, A’, N trên đường tròn lượng giác có thể được biểu diễn cho góc lượng giác nào sau đây?

$\frac{\pi }{3}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right);-\pi +k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right);-\frac{\pi }{3}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right).$

Lời giải:

– Xét góc lượng giác $\frac{\pi }{3}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$

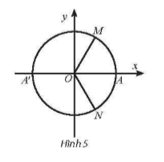
⦁ Với k = 0 ta có góc lượng giác $\alpha =\frac{\pi }{3}$, được biểu diễn bởi điểm M trên Hình 5.

⦁ Với k = 1 ta có góc lượng giác $\beta =\frac{\pi }{3}+\frac{2\pi }{3}=\pi$, được biểu diễn bởi điểm A’ trên Hình 5.

⦁ Với k = –1 ta có góc lượng giác $\gamma =\frac{\pi }{3}-\frac{2\pi }{3}=-\frac{\pi }{3}$, được biểu diễn bởi điểm N trên Hình 5.

Vậy các điểm M, A’, N trên đường tròn lượng giác có thể được biểu diễn cho góc lượng giác $\frac{\pi }{3}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$.

– Tương tự như vậy, ta cũng xác định được các điểm M, A’, N trên đường tròn lượng giác có thể được biểu diễn cho góc lượng giác $-\pi +k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$.

– Xét góc lượng giác $-\frac{\pi }{3}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right)$

Với k = 1 ta có góc lượng giác α = 0, được biểu diễn bởi điểm A, không thỏa mãn yêu cầu đề bài.

Bài 11 trang 10 SBT Toán 11 Tập 1: Cho ba điểm M, N, P lần lượt là các điểm biểu diễn trên đường tròn lượng giác của các góc lượng giác có số đo k2π;$\frac{\pi }{2}+k2\pi ;$ π + k2π (k ∈ ℤ). Tam giác MNP là tam giác gì?

Lời giải:

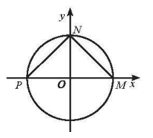
Dễ thấy M(1; 0), N(0; 1) và P(-1; 0).

Suy ra MN = NP = $\sqrt{2}$, MP = 2.

Tam giác MNP có MN = NP nên là tam giác cân tại N.

Mà MN² + NP² = 2 + 2 = 4 = MP² nên tam giác MNP vuông tại N.

Vậy tam giác MNP là tam giác vuông cân tại N.

Bài 12 trang 10 SBT Toán 11 Tập 1: Một chiếc quạt trần năm cánh quay với tốc độ 175 vòng trong một phút. Chọn chiều quay của quạt là chiều dương.

a) Sau 5 giây, cánh quạt quay được một góc có số đo bao nhiêu radian?

b) Sau thời gian bao lâu cánh quạt quay được một góc có số đo 42π?

Lời giải:

a) Sau 1 giây, cánh quạt quay được $\frac{175}{60}=\frac{35}{12}$(vòng) theo chiểu dương. Suy ra sau 1 giây, cánh quạt quay được một góc có số đo là $\frac{35}{12}\cdot 2\pi =\frac{35\pi }{6}.$

Vậy sau 5 giây, cánh quạt quay được một góc có số đo là $\frac{35\pi }{6}\cdot 5=\frac{175\pi }{6}.$

b) Thời gian để cánh quạt quay được một góc có số đo 42π là:

$42\pi :\frac{35\pi }{6}=\mathrm{7,2}$(giây).

Bài 13 trang 10 SBT Toán 11 Tập 1: Trong chặng đua nước rút, bánh xe của một vận động viên đua xe đạp quay được 30 vòng trong 8 giây. Chọn chiều quay của bánh xe là chiều dương. Xét van V của bánh xe.

a) Sau 1 phút, van V đó quay được một góc có số đo là bao nhiêu radian?

b) Biết rằng bán kính của bánh xe là 35 cm. Độ dài quãng đường mà vận động viên đua xe đạp đã đi được trong một phút là bao nhiêu mét?

Lời giải:

a) Sau 1 giây, van V của bánh xe quay được $\frac{30}{8}=\mathrm{3,75}$(vòng).

Sau 1 phút, van V của bánh xe quay được 3,75. 60 = 225 (vòng).

Suy ra sau 1 phút, van V của bánh xe quay được một góc có số đo là 225.2π = 450π.

b) Mỗi góc ở tâm với số đo 1 rad chắn một cung có độ dài bằng bán kính bánh xe r = 0,35m. Do đó độ dài quãng đường mà vận động viên đua xe đạp đã đi được trong 1 phút là: 450π.0,35 ≈ 494,8 (m).

Lý thuyết Góc lượng giác

1. Góc lượng giác

* Khái niệm góc lượng giác

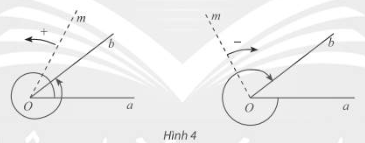
- Cho 2 tia Oa, Ob.

Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob.

Kí hiệu: (Oa, Ob).

- Khi tia Om quay một góc $\alpha$ ta nói số đo của góc lượng giác (Oa, Ob) bằng $\alpha$, kí hiệu sđ(Oa, Ob) =$\alpha$

* Chú ý:

- Với 2 tia Oa, Ob cho trước, có vô số góc lượng giác tia đầu Oa, tia cuối Ob. Ta dùng chung kí hiệu (Oa, Ob) cho tất cả các góc lượng giác này.

- Số đo các góc lượng giác có cùng tia đầu Oa, tia cuối Ob sai khác nhau một bội nguyên của 360^o có công thức là:

Sđ(Oa,Ob) = $\alpha$+ k360^o, $k\in \mathbb{Z}$.

* Hệ thức Chasles

Với 3 tia Ou, Ov, Ow bất kì ta có:

Sđ(Ou,Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) +k360^o, $k\in \mathbb{Z}$.

2. Đơn vị radian

Trên đường tròn bán kính R tùy ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (rad).

Ta có: ${180}^o=\pi$rad, do đó 1 rad $={\left(\frac{180}{\pi }\right)}^o$, $1^o=\left(\frac{\pi }{180}\right)$rad.

$\Rightarrow \alpha$ rad $={\left(\frac{180\alpha }{\pi }\right)}^o$, ${\alpha }^o=\left(\frac{\pi \alpha }{180}\right)$rad.

3. Đường tròn lượng giác

Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm O bán kính 1. Trên đường tròn này chọn điểm A(1;0) làm gốc, chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là chiều xùng chiều kim đồng hồ. Đường tròn cùng với gốc và chiều như trên gọi là đường tròn lượng giác.

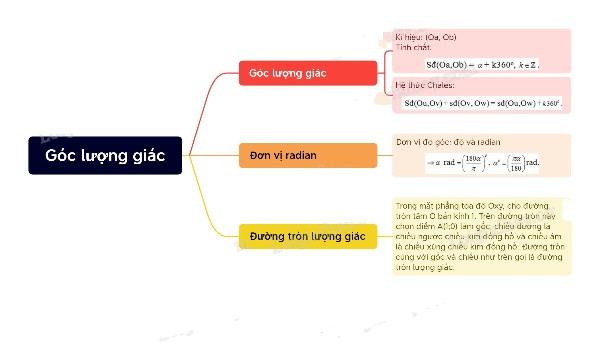
Sơ đồ tư duy Góc lượng giác

Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài 5: Phương trình lượng giác cơ bản

Bài tập cuối chương 1 trang 32