Sách bài tập Toán 11 Bài 2 (Chân trời sáng tạo): Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

Giải SBT Toán 11 Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

Bài 1 trang 158 SBT Toán 11 Tập 1: Một trang báo điện tử thống kê thời gian người sử dụng đọc thông tin trên trang trong mỗi lần truy cập ở bảng sau:

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.

Lời giải:

Cỡ mẫu n = 125.

Gọi x₁; x₂; x₃; ...; x₁₂₅ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₄₅ ∈ [0; 2); x₄₆, ..., x₇₉ ∈ [2; 4); x₈₀, ..., x₁₀₂ ∈ [4; 6);

x₁₀₃, ..., x₁₂₀ ∈ [6; 8); x₁₂₁, ..., x₁₂₅ ∈ [8; 10).

⦁ Tứ phân vị thứ hai của mẫu số liệu x₁; x₂; x₃; ...; x₁₂₅ là x₆₃ ∈ [2; 4).

Do đó, tứ phân vị thứ hai của mẫu số liệu ghép nhóm là

$Q_2=2+\frac{\frac{125}{2}-\left(45+0\right)}{34}\cdot \left(4-2\right)=\frac{103}{34}$.

⦁ Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₁₂₅ là $\frac{1}{2}\left(x_{31}+x_{32}\right)$. Do x₃₁ và x₃₂ thuộc nhóm [0; 2) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là

$Q_1=0+\frac{\frac{125}{4}-\left(0+0\right)}{45}\cdot \left(2-0\right)=\frac{25}{18}$.

⦁ Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃; ...; x₁₂₅ là $\frac{1}{2}\left(x_{94}+x_{95}\right)$. Do x₉₄ và x₉₅ thuộc nhóm [4; 6) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là

$Q_3=4+\frac{\frac{3\cdot 125}{4}-\left(34+45\right)}{23}\cdot \left(6-4\right)=\frac{243}{46}$

Bài 2 trang 158 SBT Toán 11 Tập 1: Người ta thống kê tốc độ của một số xe ô tô di chuyển qua một trạm kiểm soát trên đường cao tốc trong một khoảng thời gian ở bảng sau:

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.

Lời giải:

Cỡ mẫu n = 78.

Gọi x₁; x₂; x₃; ...; x₇₈ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₅ ∈ [75; 80); x₆, ..., x₁₇ ∈ [80; 85); x₁₈, ..., x₃₅ ∈ [85; 90); x₃₆, ..., x₅₉ ∈ [90; 95); x₆₀, ..., x₇₈ ∈ [95; 100).

⦁ Tứ phân vị thứ hai của mẫu số liệu x₁; x₂; x₃; ...; x₇₈ là $\frac{1}{2}\left(x_{39}+x_{40}\right)$. Do x₃₉ và x₄₀ thuộc nhóm [90; 95). Do đó, tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:

$Q_2=90+\frac{\frac{78}{2}-\left(5+12+18\right)}{24}\cdot \left(95-90\right)=\frac{545}{6}$.

⦁ Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₇₈ là x₂₀. Do x₂₀ thuộc nhóm [85; 90) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=85+\frac{\frac{78}{4}-\left(5+12\right)}{18}\cdot \left(90-85\right)=\frac{3085}{36}$.

⦁ Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃;...; x₇₈ là x₅₉. Do x₅₉ thuộc nhóm [90; 95) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

$Q_3=90+\frac{\frac{3\cdot 78}{4}-\left(5+12+18\right)}{24}\cdot \left(95-90\right)=\frac{4555}{48}$.

Bài 3 trang 158 SBT Toán 11 Tập 1: Thâm niên công tác của các công nhân hai nhà máy A và B.

a) Hãy so sánh thâm niên công tác của nhân viên hai nhà máy theo số trung bình và trung vị.

b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của hai mẫu số liệu ghép nhóm trên.

Lời giải:

a) Bảng tần số ghép nhóm bao gồm giá trị đại diện của các nhóm như sau:

Trung bình số năm thâm niên của công nhân nhà máy A là:

${\overline{x}}_A=\frac{2,5\cdot 35+7,5\cdot 13+12,5\cdot 12+17,5\cdot 12+22,5\cdot 8}{35+13+12+12+8}$ = $\frac{145}{16}$ = 9,0625 (năm).

Trung bình số năm thâm niên của công nhân nhà máy B là:

${\overline{x}}_B=\frac{2,5\cdot 14+7,5\cdot 26+12,5\cdot 24+17,5\cdot 11+22,5\cdot 5}{14+26+24+11+5}$ = $\frac{167}{16}$ = 10,4375 (năm).

Suy ra ${\overline{x}}_A<{\overline{x}}_B$.

Vậy nếu so sánh theo số trung bình (năm) thì thâm niên công tác của nhân viên công ty A ngắn hơn thâm niên công tác của nhân viên công ty B.

• Nhà máy A

Gọi x₁; x₂; x₃; ...; x₈₀ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₃₅ ∈ [0; 5); x₃₆, ..., x₄₈ ∈ [5; 10); x₄₉, ..., x₆₀ ∈ [10; 15);

x₆₁, ..., x₇₂ ∈ [15; 20); x₇₃, ..., x₈₀ ∈ [20; 25).

Cỡ mẫu n_A = 80 là số chẵn nên trung vị $M_e\left(A\right)=\frac{1}{2}\left(x_{40}+x_{41}\right)$. Do x₄₀ và x₄₁ thuộc nhóm [5; 10) nên trung vị của mẫu số liệu là

$M_e\left(A\right)=5+\frac{\frac{80}{2}-\left(35+0\right)}{13}\cdot \left(10-5\right)=\frac{90}{13}$.

• Nhà máy B

Gọi x₁; x₂; x₃; ...; x₈₀ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₁₄ ∈ [0; 5); x₁₅, ..., x₄₀ ∈ [5; 10); x₄₁, ..., x₆₄ ∈ [10; 15);

x₆₅, ..., x₇₅ ∈ [15; 20); x₇₆, ..., x₈₀ ∈ [20; 25).

Cỡ mẫu n_B = 80 là số chẵn nên trung vị $M_e\left(B\right)=\frac{1}{2}\left(x_{40}+x_{41}\right)$. Do x₄₀ thuộc nhóm [5; 10) và x₄₁ thuộc nhóm [10; 15) nên ta có M_e(B) = 10.

Suy ra M_e(A) < M_e(B).

Vậy nếu so sánh theo trung vị thì thâm niên công tác của nhân viên công ty A ngắn hơn thâm niên công tác của nhân viên công ty B.

b) • Nhà máy A

Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₈₀ là $\frac{1}{2}\left(x_{20}+x_{21}\right)$. Do x₂₀ và x₂₁ thuộc nhóm [0; 5) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là.

$Q_1\left(A\right)=0+\frac{\frac{80}{4}-0}{35}\cdot \left(5-0\right)=\frac{20}{7}.$

Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃;...; x₈₀ là $\frac{1}{2}\left(x_{60}+x_{61}\right)$. Do x₆₀ thuộc nhóm [10; 15) và x₆₁ thuộc nhóm [15; 20) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là Q₃(A) = 15.

• Nhà máy B

Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₈₀ là $\frac{1}{2}\left(x_{20}+x_{21}\right)$. Do x₂₀ và x₂₁ thuộc nhóm [5; 10) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là

$Q_1\left(B\right)=5+\frac{\frac{80}{4}-14}{26}\cdot \left(10-5\right)=\frac{80}{13}.$

Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃;...; x₈₀ là $\frac{1}{2}\left(x_{60}+x_{61}\right)$. Do x₆₀ và x₆₁ thuộc nhóm [10; 15) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là

$Q_3\left(B\right)=10+\frac{\frac{3\cdot 80}{4}-\left(14+26\right)}{24}\cdot \left(15-10\right)=\frac{85}{6}.$

Bài 4 trang 158 SBT Toán 11 Tập 1: Thầy giáo thống kê lại số lần kéo xà đơn của các học sinh nam khối 11 ở bảng sau:

a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.

b) Thầy giáo dự định chọn 25% học sinh có số lần kéo thấp nhất để bồi dưỡng thể lực thêm. Thầy giáo nên chọn học sinh có thành tích kéo xà đơn dưới bao nhiêu lần để bồi dưỡng thể lực?

Lời giải

a) Do số học sinh là số nguyên nên ta hiệu chỉnh lại bảng số liệu gồm giá trị đại diện như sau:

Cỡ mẫu n = 143.

• Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{8\cdot 35+13\cdot 54+18\cdot 32+23\cdot 17+28\cdot 5}{143}=\frac{2089}{143}$.

• Nhóm chứa mốt của mẫu số liệu ghép nhóm là [10,5; 15,5).

Do đó, u_m = 10,5; n_m‒1 = 35; n_m = 54; n_m+1 = 52; u_{m + 1} ‒ u_m = 15,5 ‒ 10,5 = 5.

Mốt của mẫu số liệu ghép nhóm là:

$M_O=10,5+\frac{54-35}{\left(54-35\right)+\left(54-32\right)}\cdot 5=\frac{1051}{82}$.

• Gọi x₁; x₂; x₃; ...; x₁₄₃ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₃₅ ∈ [5,5; 10,5); x₃₆, ..., x₈₉ ∈ [10,5; 15,5); x₉₀, ..., x₁₂₁ ∈ [15,5; 20,5);

x₁₂₂, ..., x₁₃₈ ∈ [20,5; 25,5); x₁₃₉, ..., x₁₄₃ ∈ [25,5; 30,5).

Cỡ mẫu n = 143 là số lẻ nên trung vị M_e = x₇₂. Do x₇₂ thuộc nhóm [10,5; 15,5) nên trung vị của mẫu số liệu là

$M_e=10,5+\frac{\frac{143}{2}-\left(35+0\right)}{54}\cdot \left(15,5-10,5\right)=\frac{1499}{108}$.

b) Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃; ...; x₁₄₃ là x₃₆. Do x₃₆ thuộc nhóm [10,5; 15,5) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là

$Q_1=10,5+\frac{\frac{143}{4}-\left(35+0\right)}{54}\cdot \left(15,5-10,5\right)=\frac{761}{72}\approx 10,57$.

Thầy giáo nên chọn các bạn có thành tích kéo xà dưới 11 lần để bồi dưỡng thể lực thêm.

Bài 5 trang 159 SBT Toán 11 Tập 1: Kết quả kiểm tra cân nặng của một số quả trứng chim cút được lựa chọn ngẫu nhiên ở hai trang trại chăn nuôi A và B được biểu diễn ở biểu đồ sau (đơn vị: g).

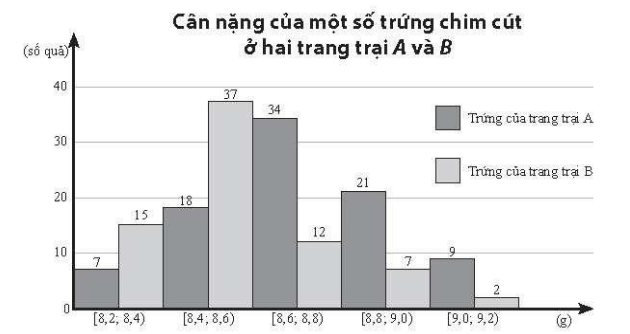
a) Hãy so sánh cân nặng của trứng chim cút của hai trang trại A và B theo số trung bình và trung vị.

b) Hãy ước lượng tứ phân vị thứ nhất và tứ phân vị thứ ba của cân nặng trứng chim cút của trang trại A.

Lời giải:

a) Từ biểu đồ đã cho, ta lập được bảng số liệu ghép nhóm sau:

Từ đó, ta có bảng thống kê số quả trứng chim cút của hai trang trại theo giá trị đại diện như sau:

⦁ Đối với trang trại A: Cỡ mẫu n_A = 89.

Cân nặng trung bình của mỗi quả trứng của mẫu số liệu ghép nhóm là

${\overline{x}}_A=\frac{8,3\cdot 7+8,5\cdot 18+8,7\cdot 34+8,9\cdot 21+9,1\cdot 9}{89}=\frac{7757}{890}\approx 8,72$ (g).

Gọi x₁; x₂; x₃;...; x₈₉ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₇ ∈ [8,2; 8,4); x₈, ..., x₂₅ ∈ [8,4; 8,6); x₂₆, ..., x₅₉ ∈ [8,6; 8,8);

x₆₀, ..., x₈₀ ∈ [8,8; 9,0); x₈₁, ..., x₈₉ ∈ [9,0; 9,2).

Cỡ mẫu n_A = 89 là số lẻ nên trung vị M_e(A) = x₄₅. Do x₄₅ thuộc nhóm [8,6; 8,8) nên trung vị của mẫu số liệu ghép nhóm là

$M_e\left(A\right)=8,6+\frac{\frac{89}{2}-\left(7+18\right)}{34}\cdot \left(8,8-8,6\right)=\frac{2963}{340}\approx 8,71$ (g).

⦁ Đối với trang trại B: Cỡ mẫu n_B = 73.

Cân nặng trung bình của mỗi quả trứng của mẫu số liệu ghép nhóm là

${\overline{x}}_B=\frac{8,3\cdot 15+8,5\cdot 37+8,7\cdot 12+8,9\cdot 7+9,1\cdot 2}{73}=\frac{6239}{730}\approx 8,55$ (g).

Gọi x₁; x₂; x₃; ...; x₇₃ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₁₅ ∈ [8,2; 8,4); x₁₆, ..., x₅₂ ∈ [8,4; 8,6); x₅₃, ..., x₆₄ ∈ [8,6; 8,8);

x₆₅, ..., x₇₁ ∈ [8,8; 9,0); x₇₂, x₇₃ ∈ [9,0; 9,2).

Cỡ mẫu n_B = 73 là số lẻ nên trung vị M_e(B) = x₃₇. Do x₃₇ thuộc nhóm [8,4; 8,6) nên trung vị của mẫu số liệu ghép nhóm là

$M_e\left(B\right)=8,4+\frac{\frac{73}{2}-15}{37}\cdot \left(8,6-8,4\right)=\frac{3151}{370}\approx 8,52$ (g).

Ta thấy ${\overline{x}}_A>{\overline{x}}_B$ và M_e (A) > M_e (B).

Vậy khi so sánh theo số trung bình hay theo trung vị, cân nặng của trứng chim cút của trang trại A đều lớn hơn cân nặng của trứng chim cút của trang trại B.

b) Đối với trang trại A:

Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₈₉ là $\frac{1}{2}\left(x_{22}+x_{23}\right)$. Do x_22­ và x₂₃ thuộc nhóm [8,4; 8,6) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là

$Q_1\left(A\right)=8,4+\frac{\frac{89}{4}-7}{18}\cdot \left(8,6-8,4\right)=\frac{617}{72}\approx 8,57$.

Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃;...; x₈₉ là $\frac{1}{2}\left(x_{66}+x_{67}\right)$. Do x_66­ và x₆₇ thuộc nhóm [8,8; 9,0), nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là

$Q_3\left(A\right)=8,8+\frac{\frac{3\cdot 89}{4}-\left(7+18+34\right)}{21}\cdot \left(9,0-8,8\right)=\frac{3727}{420}\approx 8,87$.

Lý thuyết Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

1. Trung vị

Công thức xác định trung vị của mẫu số liệu ghép nhóm:

+) Gọi n là cỡ mẫu.

+) Giả sử đó là nhóm thứ p: $[u_m;u_{m+1})$.

+) $n_m$ là tần số của nhóm chứa trung vị.

+) $C=n_1+n_2+...+n_{m-1}$.

Khi đó trung vị là:

$M_e=u_m+\frac{\frac{n}{2}-C}{n_m}.\left(u_{m+1}-u_m\right)$

* Ý nghĩa: Từ dữ liệu ghép nhóm nói chung không thể xác định chính xác trung vị của mẫu số liệu gốc. Trung vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho mẫu số liệu gốc và có thể lấy làm giá trị đại diện cho mẫu số liệu.

2. Tứ phân vị

- Để tính tứ phân vị thứ nhất $Q_1$ của mẫu số liệu ghép nhóm, ta làm như sau:

• Giả sử nhóm chứa $Q_1$ là nhóm $[u_m;u_{m+1})$.
• $n_m$ là tần số của nhóm chứa phân vị thứ nhất.
• $C=n_1+n_2+...+n_{m-1}$.

Khi đó,

$Q_1=u_m+\frac{\frac{n}{4}-C}{n_m}.\left(u_{m+1}-u_m\right)$

- Để tính tứ phân vị thứ ba $Q_3$ của mẫu số liệu ghép nhóm, ta làm như sau:

• Giả sử nhóm chứa $Q_3$ là nhóm $[{\mathrm{u}}_j;u_{j+1})$.
• $n_j$là tần số của nhóm chứa phân vị thứ nhất.
• $C=n_1+n_2+...+n_{j-1}$.

Khi đó,

$Q_3=u_j+\frac{\frac{3n}{4}-C}{n_j}.\left(u_{j+1}-u_j\right)$

- Tứ phân vị thứ hai $Q_2$ chính là trung vị $M_e$.

- Nếu tứ phân vị thứ k là $\frac{1}{2}\left(x_m+x_{m+1}\right)$, trong đó $x_m$ và $x_{m+1}$thuộc hai nhóm liên tiếp thì ta lấy $Q_k=u_j$.

* Ý nghĩa:

Bộ ba tứ phân vị của mẫu số liệu ghép nhóm là giá tị xấp xỉ cho tứ phân vị của mẫu số liệu gốc và được sử dụng làm giá trị đo xu thế trung tâm của mẫu số liệu.

Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Hai mặt phẳng song song

Bài 5: Phép chiếu song song

Bài tập cuối chương 4 trang 132

Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm

Bài tập cuối chương 5 trang 160