Giải các phương trình lượng giác sau: a) sin(3x+pi/6) = căn 3 /2
Lời giải Bài 1 trang 30 SBT Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.
Giải SBT Toán 11 Bài 5: Phương trình lượng giác cơ bản
Bài 1 trang 30 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:
a)
b) cos(2x ‒ 30°) = ‒1;
c) 3sin(‒2x + 17°) = 4;
d)
e)
g)
*Lời giải:
a)
hoặc
hoặc
Vậy phương trình có nghiệm là và
b) cos(2x ‒ 30°) = ‒1
⇔ 2x ‒ 30° = 180° + k360° (k ∈ ℤ)
⇔ 2x = 210 + k360° (k ∈ ℤ)
⇔ x = 105° + k180° (k ∈ ℤ)
Vậy phương trình có nghiệm là x = 105° + k180° (k ∈ ℤ).
c) 3sin(‒2x + 17°) = 4
Do nên phương trình vô nghiệm.
d)
hoặc
hoặc
hoặc
Vậy phương trình có nghiệm là và
e)
Vậy phương trình có nghiệm là
g)
Vậy phương trình có nghiệm là
*Phương pháp giải:
- Vận dụng các kiến thức và cách giải của các phương trình lượng giác cơ bản để giải tìm ra nghiệm
* Lý thuyết cần nắm và một số phương trình lượng giác thường gặp:
a) Phương trình bậc nhất đối với một hàm số lượng giác
*Phương pháp giải:
Chuyển vế rồi chia hai vế của phương trình dạng at+b=0 (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.
b) Phương trình bậc hai đối với một hàm số lượng giác
*Phương pháp giải:
Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này. Cuối cùng ta đưa về việc giải các phương trình lượng giác cơ bản.
1. Hàm số y = sinx.
Từ định nghĩa ta thấy hàm số y = sinx :
+ Xác định với mọi x và – 1 ≤ sinx ≤ 1.
+ Là hàm số lẻ.
+ Là hàm số tuần hoàn với chu kì 2π.
Sau đây, ta sẽ khảo sát sự biến thiên của hàm số y = sinx.
a) Sự biến thiên và đồ thị hàm số y = sinx trên đoạn [0; π].
Hàm số y = sinx đồng biến trên và nghịch biến trên .
Bảng biến thiên:
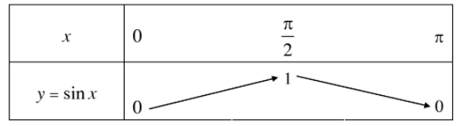
Đồ thị của hàm số y = sinx trên đoạn [0; π] đi qua các điểm (0; 0); (x1; sinx1); (x2; sinx2); (x3; sinx3); (x4; sinx4); (π; 0).
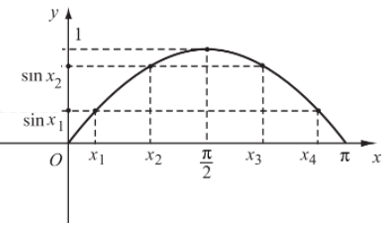
c) Tập giá trị của hàm số y = sinx
Tập giá trị của hàm số này là [– 1; 1].
2. Hàm số y = cosx.
Từ định nghĩa ta thấy hàm số y = cosx:
+ Xác định với mọi x và – 1 ≤ cosx ≤ 1.
+ Là hàm số chẵn.
+ Là hàm số tuần hoàn với chu kì 2π.
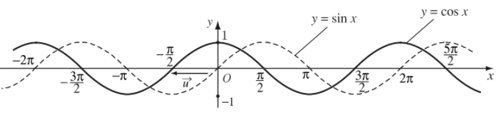
Với mọi x ta có: .
Từ đó, bằng cách tịnh tiến đồ thị hàm số y = sinx theo vecto (sang trái một đoạn có độ dài bằng , song song với trục hoành), ta được đồ thị hàm số y = cos x.
+ Hàm số y = cos x đồng biến trên đoạn [– π; 0] và nghịch biến trên đoạn [0; π].
+ Bảng biến thiên:
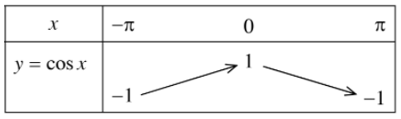
+ Tập giá trị của hàm số y = cosx là [– 1; 1].
+ Đồ thị của các hàm số y = cosx; y = sinx được gọi chung là các đường hình sin.
3. Hàm số y = tanx.
Từ định nghĩa hàm số y = tan x:
+ Có tập xác định: .
+ Là hàm số lẻ.
+ Là hàm số tuần hoàn với chu kì π.
Sự biến thiên và đồ thị hàm số y = tanx trên nửa khoảng
+ Hàm số y = tanx đồng biến trên nửa khoảng .
+ Bảng biến thiên:
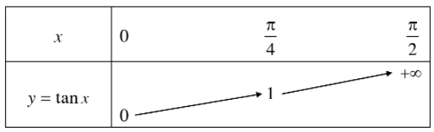
+ Bảng giá trị:
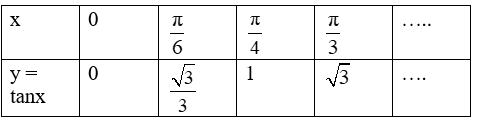
Đồ thị hàm số y = tanx trên nửa khoảng đi qua các điểm tìm được.
4. Hàm số y = cot x
Hàm số y = cotx:
+ Có tập xác định là .
+ Là hàm số lẻ.
+ Là hàm số tuần hoàn với chu kì π.
Sự biến thiên của hàm số y = cotx trên khoảng (0; π).
Hàm số y = cotx nghịch biến trên khoàn (0; π).
Bảng biến thiên:
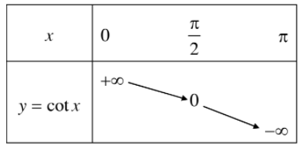
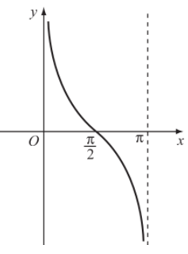
Hình biểu diễn của hàm số y = cotx trên khoảng (0; π).
Xem thêm các bài viết liên quan hay, chi tiết:
Chuyên đề Phương trình lượng giác cơ bản - Toán 11
TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án) – Toán 11
Trắc nghiệm Một số phương trình lượng giác thường gặp (có đáp án)
Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 30 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau: a) ...
Bài 2 trang 31 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau: a) cos(2x + 10°) = sin(50° ‒ x);...
Bài 3 trang 31 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:...
Bài 4 trang 31 SBT Toán 11 Tập 1: Tìm tập xác định của hàm số lượng giác...
Bài 5 trang 31 SBT Toán 11 Tập 1: Tìm các nghiệm của mỗi phương trình sau trong khoảng (‒π; π)...
Bài 6 trang 31 SBT Toán 11 Tập 1: Tìm hoành độ các giao điểm của đồ thị các hàm số sau:...
Bài 7 trang 31 SBT Toán 11 Tập 1: Tìm hoành độ các giao điểm của đồ thị hàm số ...
Bài 9 trang 32 SBT Toán 11 Tập 1: Một quả bóng được ném xiên một góc alpha...
Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Giá trị lượng giác của một góc lượng giác
Bài 3: Các công thức lượng giác
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo
