Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 64 Tập 2 Kết nối tri thức

    Với giải bài tập Toán lớp 7 trang 64 Tập 2 trong Bài 32: Quan hệ đường giữa đường vuông góc và đường xiên sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 64 Tập 2.

    1 886 08/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 64 Tập 2

    Hoạt động trang 64 Toán 7 Tập 2:

    Cho điểm A không nằm trên đường thẳng d.

    a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.

    b) Em hãy giải thích vì sao AH < AM.

    Lời giải:

    a) 

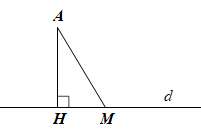
    Giải Toán 7 Bài 32 (Kết nối tri thức): Quan hệ đường giữa đường vuông góc và đường xiên (ảnh 1) 

    b) Do AH ⊥ d nên AHM^ = 90°.

    Nên tam giác AHM là tam giác vuông có AM là cạnh huyền.

    Mà trong tam giác vuông cạnh huyền là cạnh lớn nhất nên AM > AH.

    Luyện tập trang 64 Toán 7 Tập 2:

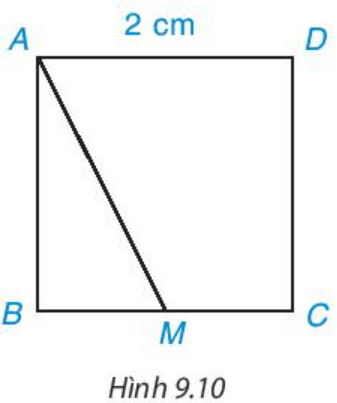
    Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.

    a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.

    b) So sánh hai đoạn thẳng AB và AM.

    c) Tìm khoảng cách từ điểm C đến đường thẳng AB.

    Giải Toán 7 Bài 32 (Kết nối tri thức): Quan hệ đường giữa đường vuông góc và đường xiên (ảnh 1) 

    Lời giải:

    a) Đường vuông góc kẻ từ A đến đường thẳng BC là đoạn thẳng AB.

    Đường xiên kẻ từ A đến đường thẳng BC là đoạn thẳng AM.

    b) Do AM là đường xiên kẻ từ A đến BC và AB là đường vuông góc kẻ từ A đến BC nên AM > AB.

    c) Đường vuông góc kẻ từ điểm C đến đường thẳng AB là đoạn thẳng CB.

    Do đó khoảng cách từ C đến đường thẳng AB bằng độ dài đoạn thẳng BC.

    Do ABCD là hình vuông nên BC = AD = 2 cm.

    Vậy khoảng cách từ C đến đường thẳng AB bằng 2 cm.

    Vận dụng trang 64 Toán 7 Tập 2:

    Em hãy trả lời câu hỏi trong tình huống mở đầu.

    Lời giải:

    Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì quãng đường bơi phải ngắn nhất.

    Bài toán đưa về tìm đoạn ngắn nhất trong ba đoạn thẳng OA, OB và OC.

    Ta có OA là đường vuông góc kẻ từ O đến AC.

              OB và OC là các đường xiên kẻ từ O đến AC

    Do đó OA là đoạn thẳng có độ dài ngắn nhất.

    Vậy để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.

    Thử thách nhỏ trang 64 Toán 7 Tập 2:

    a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.

    Giải Toán 7 Bài 32 (Kết nối tri thức): Quan hệ đường giữa đường vuông góc và đường xiên (ảnh 1) 

    b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?

    Lời giải:

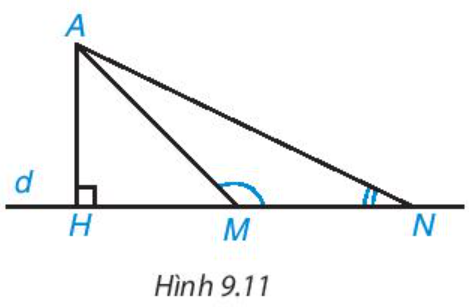
    a) Xét ∆AHM có HM < HN thì AMN^ là góc ngoài tại đỉnh M của ∆AHM

    Do đó AMN^=AHM^+HAM^>AHM^.

    Mà AHM^=90° nên AMN^>90° là góc tù.

    Xét ∆AMN có AMN^ là góc tù nên AMN^ là góc lớn nhất trong ∆AMN.

    Do đó AN là cạnh lớn nhất trong ∆AMN hay AM < AN.

    b)

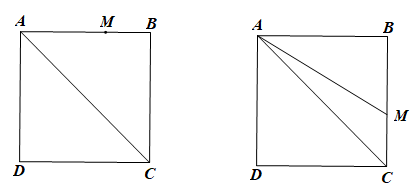
    Giải Toán 7 Bài 32 (Kết nối tri thức): Quan hệ đường giữa đường vuông góc và đường xiên (ảnh 1) 

    • Nếu M nằm trên AB thì AM ≤ AB.

    Tương tự, nếu M nằm trên AD thì AM ≤ AD.

    Mà AB = AD (do ABCD là hình vuông)

    Do đó nếu M nằm trên cạnh AB hoặc AD thì AM ≤ AB (1).

    • Nếu M nằm trên BC thì BM ≤ BC

    Theo câu a, khi đó ta có AM ≤ AC.

    Tương tự, nếu M nằm trên DC thì AM ≤ AC

    Do đó nếu M nằm trên cạnh BC hoặc DC thì AM ≤ AC (2).

    • Ta có AB là đường vuông góc kẻ từ A đến BC, AC là đường xiên kẻ từ A đến BC nên

    AC ≥ AB (3).

    Do đó từ (1), (2) và (3) suy ra AM ≤ AB ≤ AC.

    Khi đó AM lớn nhất khi AM = AC, tức điểm M trùng điểm C.

    Vậy điểm M trùng điểm C thì AM lớn nhất.

    Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

    Giải Toán 7 trang 64 Tập 2

    Giải Toán 7 trang 65 Tập 2

    Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

    Bài 33: Quan hệ giữa ba cạnh của một tam giác

    Luyện tập chung trang 71

    Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác

    Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

    Luyện tập chung trang 83

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 886 08/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: