Nội dung bài viết

    Xem thêm

    Luyện tập 2 trang 81 Toán 7 Tập 2 | Kết nối tri thức Giải Toán lớp 7

    Lời giải Luyện tập 2 trang 81 Toán 7 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 912 23/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 Kết nối tri thức  Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

    Luyện tập 2 trang 81 Toán 7 Tập 2:

    a) Chứng minh rằng trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.

    b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.

    Lời giải:

    a)

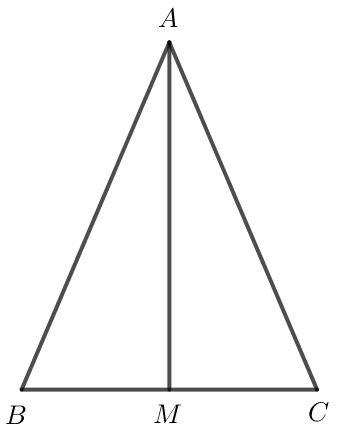
    Giải Toán 7 Bài 35 (Kết nối tri thức): Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác (ảnh 1) 

    Gọi M là trung điểm của BC.

    Khi đó M nằm trên đường trung trực của BC (1)

    Do DABC cân tại A nên AB = AC (tính chất tam giác cân)

    Do đó A nằm trên đường trung trực của BC (2)

    Từ (1) và (2) suy ra AM là đường trung trực của BC nên AM ⊥ BC.

    Vì vậy AM là đường cao của tam giác ABC.

    Xét ∆ABM và ∆ACM có:

    AB = AC (do ∆ABC cân tại A),

    AM là cạnh chung

    BM = CM (do M là trung điểm của BC),

    Do đó ∆ABM = ∆ACM (c.c.c)

    Suy ra MAB^=MAC^ (hai góc tương ứng)

    Nên AM là tia phân giác của góc BAC.

    Vậy đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác ABC.

    b)

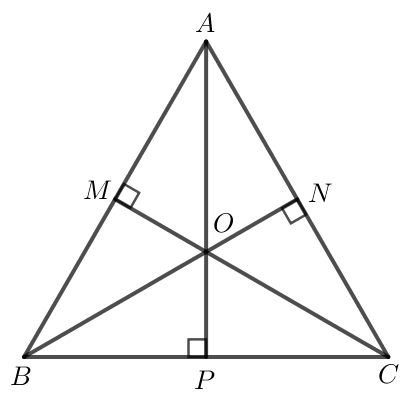
    Giải Toán 7 Bài 35 (Kết nối tri thức): Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác (ảnh 1) 

    Giả sử ∆ABC đều có O là điểm cách đều ba đỉnh của tam giác đó.

    Suy ra O là giao điểm của ba đường trung trực của ∆ABC.

    Hay AO, BO, CO lần lượt là đường trung trực của các cạnh BC, AC, AB.

    Do ∆ABC đều nên ∆ABC cân tại A.

    Do đó theo câu a), ba đường trung trực AO, BO, CO của các cạnh BC, AC, AB lần lượt là đường phân giác xuất phát từ đỉnh A, đỉnh B, đỉnh C của DABC.

    Mà ba đường phân giác AO, BO, CO cắt nhau tại O nên O cách đều ba cạnh của tam giác.

    Vậy trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.

    Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

    Mở đầu trang 77 Toán 7 Tập 2: Có thể coi ba ngôi nhà của ba anh em trong một khu vườn là ba đỉnh của một tam giác...

    Câu hỏi trang 77 Toán 7 Tập 2: Mỗi tam giác có mấy đường trung trực...

    Hoạt động 1 trang 78 Toán 7 Tập 2: Vẽ tam giác ABC (không tù) và ba đường trung trực của các đoạn thẳng BC, CA, AB...

    Hoạt động 2 trang 78 Toán 7 Tập 2: Dùng tính chất đường trung trực của một đoạn thẳng, hãy lập luận để suy ra tính chất nói ở HĐ1...

    Luyện tập 1 trang 79 Toán 7 Tập 2: Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó...

    Vận dụng 1 trang 79 Toán 7 Tập 2: Em hãy trả lời câu hỏi trong tình huống mở đầu...

    Thử thách nhỏ trang 79 Toán 7 Tập 2: Sử dụng tính chất đường trung trực của một đoạn thẳng, hãy giải thích nếu điểm Q...

    Câu hỏi trang 79 Toán 7 Tập 2: Mỗi tam giác có mấy đường cao...

    Hoạt động 3 trang 79 Toán 7 Tập 2: Vẽ tam giác ABC và ba đường cao của nó. Quan sát hình và cho biết, ba đường cao đó...

    Luyện tập 2 trang 81 Toán 7 Tập 2: a) Chứng minh rằng trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao...

    Bài 9.26 trang 81 Toán 7 Tập 2: Gọi H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HBC, HCA, HAB...

    Bài 9.27 trang 81 Toán 7 Tập 2: Cho tam giác ABC có  = 100o và trực tâm H. Tính góc BHC...

    Bài 9.28 trang 81 Toán 7 Tập 2: Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC...

    Bài 9.29 trang 81 Toán 7 Tập 2: a) Có một chi tiết máy (đường viền ngoài là đường tròn) bị gãy (H.9.46). Làm thế nào để xác định...

    Bài 9.30 trang 81 Toán 7 Tập 2: Cho hai đường thẳng không vuông góc b, c cắt nhau tại điểm A và cho điểm H không thuộc b và c...

    Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

    Luyện tập chung trang 83

    Bài tập cuối chương 9

    Bài 1: Tập hợp các số hữu tỉ

    Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

    Luyện tập chung trang 14, 15

     

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 912 23/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: