Nội dung bài viết

    Xem thêm

    Bài 3.25 trang 57 Toán 7 Tập 1 | Kết nối tri thức Giải Toán lớp 7

    Bài 3.25 trang 57 Toán 7 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 7 Tập 1.

    1 4,058 06/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán lớp 7 Bài 11: Định lí và chứng minh định lí

    Bài 3.25 trang 57 Toán 7 Tập 1: Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?

    Trả lời:

    GT

    a // b, c⊥a;   

    c cắt a tại A, c cắt b tại B;

    Góc aAc và góc bBc là hai góc đồng vị.

    KL

    c⊥b.  
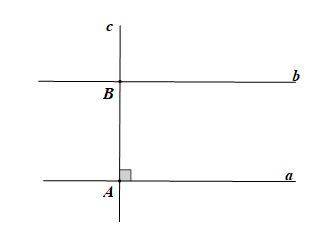
    Tài liệu VietJack

    +) Chứng minh (Hình vẽ trên):

    Theo giả thiết ta có c⊥a tại A nên aAc^=90°. 

    Từ a // b suy ra aAc^=bBc^ (hai góc đồng vị).

    Mà aAc^=90°, do đó bBc^=90°.

    Suy ra c⊥b tại B.

    Vậy c⊥b

    +) Trong chứng minh trên ta đã sử dụng những điều đúng đã biết sau:

    - Hai đường thẳng vuông góc với nhau tạo thành các góc có số đo bằng 90°.

    - Một đường thắng cắt hai đường thẳng song song với nhau tạo thành cặp góc đồng vị có số đo bằng nhau. 

    Video giải bài tập Toán 7 Bài 11 Định lí và chứng minh định lí

    Xem thêm lời giải bài tập Toán lớp 7 Bài 11 Kết nối tri thức hay, chi tiết khác:

    Mở đầu trang 55 Toán 7 Tập 1: Trong Bài 10, ta đã dùng cách đo đạc để kiểm nghiệm tính chất sau là đúng...

    Luyện tập 1 trang 56 Toán 7 Tập 1: Vẽ hình và viết giả thiết, kết luận của định lí: “Hai góc đối đỉnh thì bằng nhau”....

    Luyện tập 2 trang 57 Toán 7 Tập 1: Em hãy chứng minh định lí: “Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”...

    Tranh luận trang 57 Toán 7 Tập 1: Hình tròn: Hai góc đối đỉnh thì chắc chắn bằng nhau rồi...

    Bài 3.24 trang 57 Toán 7 Tập 1: Có thể coi định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng...

    Bài 3.26 trang 57 Toán 7 Tập 1: Cho góc xOy không phải góc bẹt. Khẳng định nào sau đây là đúng... 

    Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

    Luyện tập chung trang 58

    Bài tập cuối chương 3 trang 59

    Bài 12: Tổng các góc trong một tam giác

    Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

    Luyện tập chung trang 68, trang 69

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 4,058 06/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: