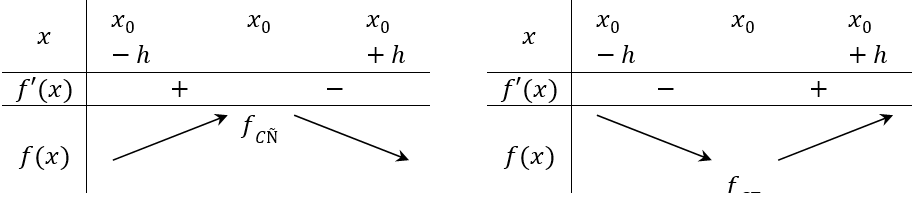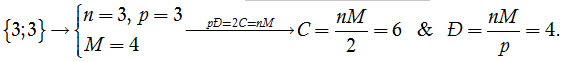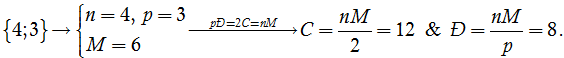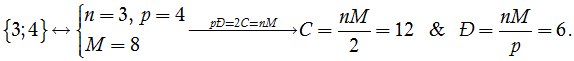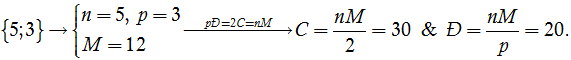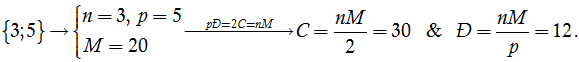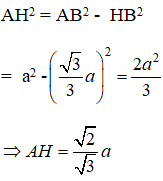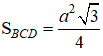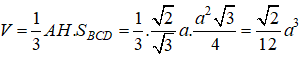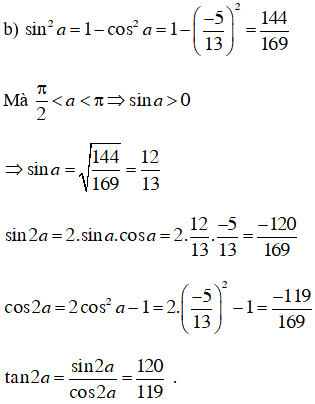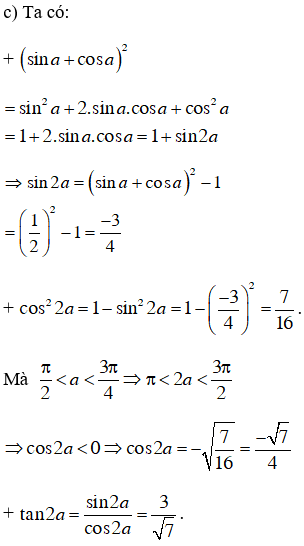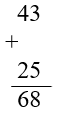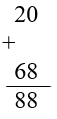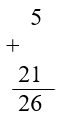Tổng hợp câu hỏi môn Toán (phần 2)
-
116 lượt thi
-
33 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
17/01/2025Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
 Xem đáp án
Xem đáp án
*Lời giải:
Khối lăng trụ đã cho là lăng trụ đứng có cạnh bên bằng a, đáy là tam giác đều cạnh a.
Gọi V là thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng a, khi đó:
*Phương pháp giải:
- dựa theo công thức tính thể tích hình lăng trụ
* Lý thuyết và các dạng bài về tính thể tích khối lăng trụ:
Các lăng trụ đặc biệt
a) Lăng trụ đứng: Là lăng trụ có cạnh bên vuông góc với đáy. Các mặt bên là các hình chữ nhật. Cạnh bên bằng đường cao của lăng trụ.
b) Lăng trụ đều: Là lăng trụ đứng và có đáy là đa giác đều. Các mặt bên của lăng trụ đều là các hình chữ nhật và bằng nhau.
c) Hình hộp: Là hình lăng trụ có đáy là hình bình hành.
+) 6 mặt của hình hộp là các hình bình hành.
+) Hai mặt đối diện song song và bằng nhau.
+) Bốn đường chéo của hình hộp đồng quy tại trung điểm của mỗi đường.
d) Hình hộp chữ nhật: là hình hộp có 6 mặt đều là các hình chữ nhật.
e) Hình lập phương: Là hình hộp có 6 mặt đều là các hình vuông (bằng nhau).
Công thức thể tích:
a) Thể tích khối lăng trụ
với: S: Diện tích đáy
h: Chiều cao.
b) Thể tích khối hộp chữ nhật
với a, b, c là ba kích thước.
c) Thể tích khối lập phương
Trong đó a là độ dài cạnh.
PHƯƠNG PHÁP TÍNH THỂ TÍCH LĂNG TRỤ
Bước 1: Xác định và tính chiều cao của khối đa diện
Bước 2: Tìm diện tích đáy bằng các công thức.
Bước 3: Sử dụng công thức tính thể tích.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Ôn tập chương 1 – Toán 12
Câu 2:
17/01/2025Tính độ dài đoạn thẳng AB biết rằng I là trung điểm của đoạn thẳng AB và AI = 8 cm.
 Xem đáp án
Xem đáp án
Lời giải:
Vì I là trung điểm của đoạn thẳng AB nên IA = IB = .
Do đó AB = 2 . AI = 2 . 8 = 16 cm.
Vậy AB = 16 cm.
Hình minh họa:

*Phương pháp giải:
- Nếu điểm I nằm giữa hai điểm A và B sao cho IA = IB thì I gọi là trung điểm của đoạn thẳng AB.
Khi đó:
IA = IB = 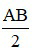 .
.

* Lý thuyết cần nắm:
- Đoạn thẳng AB, hay đoạn thẳng BA, là hình gồm 2 điểm A, B cùng với tất cả các điểm nằm giữa A và B.
- A; B là hai đầu mút (mút) của đoạn thẳng AB.
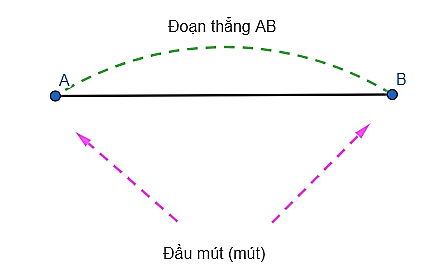
- Nếu điểm I nằm giữa hai điểm A và B sao cho IA = IB thì I gọi là trung điểm của đoạn thẳng AB.
Khi đó:
IA = IB = 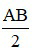 .
.

Độ dài đoạn thẳng
- Mỗi đoạn thẳng có một độ dài. Khi chọn một đơn vị độ dài thì độ dài mỗi đoạn thẳng được biểu diễn bởi một số dương (thường viết kèm đơn vị).
- Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B. Ta quy ước khoảng cách giữa hai điểm trùng nhau bằng 0 (đơn vị).
- Đơn vị đo độ dài đoạn thẳng: mm; cm; dm; m; km…
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Trung điểm của đoạn thẳng – Toán lớp 6 Kết nối tri thức
Giải Toán 6 Bài 35 (Kết nối tri thức): Trung điểm của đoạn thẳng
Câu 3:
17/01/2025Tìm m để giá trị nhỏ nhất của hàm số y=x3−3mx2+6 trên đoạn [0;3] bằng 2 .
 Xem đáp án
Xem đáp án
Đáp án đúng : D
*Lời giải:
*Phương pháp giải:
- Để xét điểm cực trị hàm số, ta sẽ:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
* Các lý thuyết thêm và các dạng bài toán về cực trị hàm số:
1.Định nghĩa: Cho hàm số y = f(x)xác định và liên tục trên khoảng (a;b) (có thể a là -∞; b là +∞) và điểm x0∈(a;b).
Nếu tồn tại số h > 0 sao cho f(x)< f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x≠x_0 thì ta nói hàm số f(x) đạt cực đại tại x0.
Nếu tồn tại số h >0 sao cho f(x) >f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x ≠ x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.
2.Điều kiện đủ để hàm số có cực trị: Giả sử hàm số y=f(x) liên tục trên
K=(x0 - h;x0 + h)và có đạo hàm trên K hoặc trên K\{x0}, với h >0.
Nếu f'(x)> 0 trên khoảng (x0 - h;x0) và f'(x) <0 trên (x0;x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
Nếu f'(x) < 0 trên khoảng (x0 - h;x0) và f'(x) >0 trên (x0;x0+ h) thì x0 là một điểm cực tiểu của hàm số f(x).
Minh họa bằng bảng biến thiến
Chú ý.
Nếu hàm sốy=f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCÑ (fCT), còn điểm M(x0;f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
DẠNG 1:Tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệuxi (i=1,2,3,...)là các nghiệm của nó.
Bước 3. Tính f''(x) và f''(xi ) .
Bước 4. Dựa vào dấu của f''(xi )suy ra tính chất cực trị của điểm xi.
DẠNG 2:Tìm tham số m để hàm số đạt cực trị tại một điểm
Trong dạng toán này ta chỉ xét trường hợp hàm số có đạo hàm tại x0.
Khi đó để giải bài toán này, ta tiến hành theo hai bước.
Bước 1. Điều kiện cần để hàm số đạt cực trị tại x0 là y'(x0) = 0, từ điều kiện này ta tìm được giá trị của tham số .
Bước 2. Kiểm lại bằng cách dùng một trong hai quy tắc tìm cực trị ,để xét xem giá trị của tham số vừa tìm được có thỏa mãn yêu cầu của bài toán hay không?
DẠNG 3:Biện luận theo m số cực trị của hàm số
1. Cực trị của hàm số bậc ba
Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y' = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ'y' = b2 - 3ac
Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
Hàm số bậc 3 không có cực trị ⇔ b2 - 3ac ≤ 0
Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
Hàm số bậc 3 có 2 cực trị ⇔ b2 - 3ac > 0
2. Cực trị của hàm số bậc bốn trùng phương
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
y' = 4ax3 + 2bx; y' = 0 ⇔
(C)có một điểm cực trị y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.
(C)có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12
Cực trị của hàm số và cách giải các dạng bài tập (2024) mới nhất
Câu 4:
18/01/2025Cho khối đa diện đều loại {3;4}. Tổng các góc phẳng tại một đỉnh của khối đa điện đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải
Khối đa diện đều loại {3;4} là khối bát diện đều. Mỗi đỉnh là đỉnh chung của 4 mặt.
Vậy tổng các góc phẳng tại một đỉnh của khối đa diện đó bằng
.
*Phương pháp giải
Dựa vào lí thuyết hoặc bảng dưới đây

*Lý thuyết nắm thêm về khối đa diện đều:

Chú ý. Gọi Đ là tổng số đỉnh, C là tổng số cạnh và M là tổng các mặt của khối đa diện đều loại {n; p}. Ta có pĐ = 2C = nM
- Xét tứ diện đều
- Xét khối lập phương
- Xét bát diện đều
- Xét khối mười hai mặt đều
- Xét khối hai mươi mặt đều
*) Các dạng bài về khối đa diện:
a) Nhận diện khối đa diện
b) Tính thể tích khối chóp có cạnh bên vuông góc với đáy
+ Một hình chóp có một cạnh bên vuông góc với đáy thì cạnh bên đó chính là đường cao.
+ Một hình chóp có hai mặt bên kề nhau cùng vuông góc với đáy thì cạnh bên là giao tuyến của hai mặt đó vuông góc với đáy
c) Tính thể tích khối lăng trụ đứng, lăng trụ đều
+) Khối lăng trụ đứng
Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.
Tính chất:
+ Các mặt bên hình lăng trụ đứng là hình chữ nhật
+ Các mặt bên hình lăng trụ đứng vuông góc với mặt đáy
+ Chiều cao là cạnh bên
+) Khối lăng trụ đều
Định nghĩa: Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều
Tính chất:
+ Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau
+ Chiều cao là cạnh bên.
Xem thêm một số bài viết liên quan hay, chi tiết:
Câu 5:
18/01/2025Cho khối chữ nhật ABCD.A'B'C'D' có thể tích V. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải:
Ta có V=AB. BC. AA'.
*Phương pháp giải:
- Nắm lại kiến thức về hình hộp chữ nhật
*Một số lý thuyết cần nắm về hình hộp chữ nhật:
a) Hình hộp chữ nhật
Định nghĩa: Hình hộp chữ nhật là hình không gian có 6 mặt đều là những hình chữ nhật.
+ Hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh.
+ Hai mặt đối diện nhau được xem là mặt đáy của hình hộp chữ nhật, các mặt còn lại được gọi là mặt bên
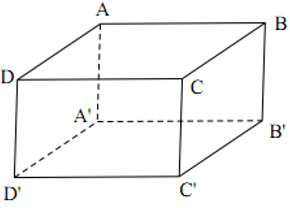
+ Hình lập phương là hình hộp chữ nhật có 6 mặt đều là những hình vuông.
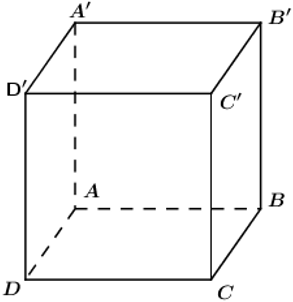
b) Mặt phẳng và đường thẳng
+ Qua ba điểm không thẳng hàng xác định một và chỉ một mặt phẳng.
+ Qua hai đường thẳng cắt nhau xác định một và chỉ một mặt phẳng.
+ Đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đó đều thuộc mặt phẳng.
c) Hai đường thẳng song song trong không gian:
+ Hai đường thẳng a, b gọi là song song với nhau nếu chúng cùng nằm trong một mặt phẳng và không có điểm chung. Kí hiệu a // b.
+ Hai đường thẳng phân biệt, cùng song song với một đường thẳng thứ ba thì song song với nhau.
Chú ý: Hai đường thẳng phân biệt trong không gian có thể:
– Cắt nhau – Song song – Chéo nhau (không cùng nằm trong một mặt phẳng)
Xem thêm các bài viết liên quan hay, chi tiết
Trắc nghiệm Hình hộp chữ nhật có đáp án (Nhận biết)
Câu 6:
18/01/2025Cho mặt cầu bán kính R ngoại tiếp một hình lập phương cạnh a. Mệnh đề nào dưới đây đúng ?
 Xem đáp án
Xem đáp án
*Lời giải:
*Phương pháp giải:
- Tính bán kính khối cầu
- Áp dụng công thức tính thể tích khối cầu để tính: S=4.pi.R2
Diện tích mặt cầu và thể tích khối cầu
Cho mặt cầu S(I; R).
Diện tích mặt cầu:
Thể tích khối cầu:
Dạng 1: Mặt cầu ngoại tiếp hình chóp
* Phương pháp giải:
- Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).
- Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục ∆ của đường tròn ngoại tiếp một đa giác của mặt bên).
- Giao điểm I của (P) và d (hoặc của ∆ và d) là tâm mặt cầu ngoại tiếp.
- Kết luận: I là tâm mặt cầu ngoại tiếp chóp.
Dạng 1.1: Hình chóp có các điểm cùng nhìn một cạnh của hình chóp dưới một góc vuông.
+) Hình chóp tam giác:
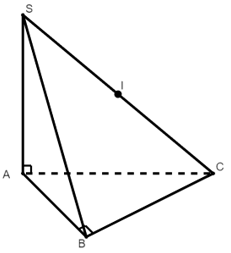
A, B cùng nhìn SC dưới một góc vuông
Tâm mặt cầu ngoại tiếp hình chóp S.ABC là trung điểm I của SC
Bán kính là:
+) Hình chóp tứ giác
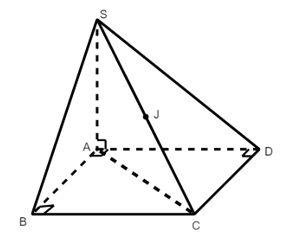
A, B, D cùng nhìn SC dưới một góc vuông
Tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm J của SC
Bán kính mặt cầu là:
Dạng 1.2: Hình chóp có mặt bên vuông góc với mặt phẳng đáy
* Phương pháp giải: Gọi h là chiều cao hình chóp và là bán kính của đường tròn ngoại tiếp mặt bên, mặt đáy và là độ dài cạnh chung của mặt bên vuông góc với đáy thì bán kính mặt cầu là:
Dạng 1.3: Mặt cầu nội tiếp khối đa diện
* Phương pháp giải: Nếu đặt V là thể tích khối chóp và là tổng diện tích mặt đáy và các mặt bên của chóp thì bán kính r của mặt cầu nội tiếp khối chóp:
Xem thêm các bài viết liên quan hay, chi tiết
Các bài toán thực tế hình không gian (có đáp án)
Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)
Câu 7:
18/01/2025Cho hình chóp có 20 cạnh. Tính số mặt của hình chóp đó.
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải:
Số cạnh bên của hình chóp bằng số cạnh đáy.
Suy ra số cạnh bên của hình chóp là: cạnh.
Vậy hình chóp có 10 mặt bên và 1 mặt đáy.
*Phương pháp giải:
- Nắm lại định nghĩa, tính chất của hình chóp
*Một số lý thuyết liên quan hình chóp tứ giác đều:
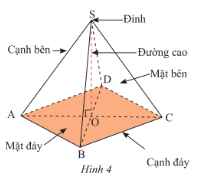
Hình chóp tứ giác đều có:
- Đáy là hình vuông.
- 4 cạnh bên bằng nhau.
- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
- Chân đường cao trùng với giao điểm của hai đường chéo của mặt đáy.
* Công thức tính diện tích xung quanh của hình chóp tứ giác đều
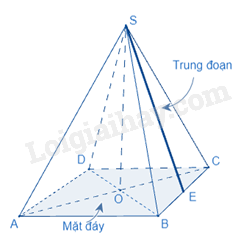
Diện tích xung quanh của hình chóp tam giác đều bằng nửa chu vi đáy với độ dài trung đoạn.
( là diện tích xung quanh, p là nửa chu vi đáy, d là trung đoạn)
* Công thức tính thể tích của hình chóp tứ giác đều
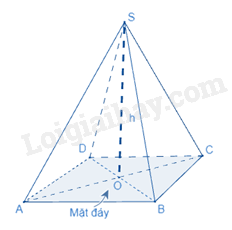
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng diện tích đáy nhân với chiều cao.
(V là thể tích, là diện tích đáy, h là chiều cao)
Xem thêm các bài viết liên quan hay, chi tiết
Trắc nghiệm Diện tích xung quanh hình chóp đều Toán 8(có đáp án)
Câu 8:
18/01/2025Diện tích mặt cầu ngoại tiếp khối hộp chữ nhật có kích thước a;a√3;2a là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
* Lời giải:
Bán kính mặt cầu ngoại tiếp khối hộp chữ nhật là:
Vậy diện tích mặt cầu là:
* Phương pháp giải:
- Tính độ dài bán kính và tính ra diện tích mặt cầu
*Một số lý thuyết và dạng bài tập về mặt cầu, mặt nón, mặt trụ:
1_MẶT NÓN:
Hình nón tròn xoay và khối nón tròn xoay.
a) Cho tam giác OIM vuông tại I. Khi quay tam giác đó xung quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.
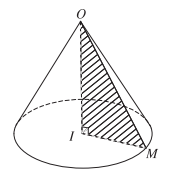
Hình tròn tâm I sinh bởi các điểm thuộc cạnh IM khi quay quanh trục OI được gọi là mặt đáy của hình nón, điểm O được gọi là đỉnh của hình nón.
Độ dài đoạn OI gọi là chiều cao của hình nón, đó cũng chính là khoảng cách từ O đến mặt phẳng đáy. Độ dài đoạn OM gọi là độ dài đường sinh của hình nón.
Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh OM khi quay quanh OI được gọi là mặt xung quanh của hình nón đó.
Diện tích xung quanh của hình nón tròn xoay.
a) Một hình chóp được gọi là nội tiếp một hình nón nếu đáy của hình chóp là đa giác nội tiếp đường tròn đáy của hình nón và đỉnh của hình chóp là đỉnh của hình nón. Khi đó, ta còn nói hình nón ngoại tiếp hình chóp.
a_Định nghĩa: Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.
Công thức tính diện tích xung quanh của hình nón.
- Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh.
(r là bán kính đường tròn đáy, l là độ dài đường sinh).
- Người ta gọi tổng của diện tích xung quanh và diện tích đáy là diện tích toàn phần của hình nón.
- Chú ý: Diện tích xung quanh, diện tích toàn phần của hình nón tròn xoay cũng là diện tích xung quanh , diện tích toàn phần của khối nón được giới hạn bởi hình nón đó.
Thể tích khối nón tròn xoay.
a) Định nghĩa.
Thể tích của khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính thể tích khối nón tròn xoay.
Gọi V là thể tích của khối nón tròn xoay có diện tích đáy B và chiều cao h, ta có công thức:
Như vậy, nếu bán kính đáy bằng r thì , khi đó: .
2_MẶT TRỤ
a) Định nghĩa
Trong mặt phẳng (P) cho hai đường thẳng ∆ và l song song với nhau, cách nhau một khoảng bằng r. Khi quay mặt phẳng (P) xung quanh ∆ thì đường thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay.
Người ta thường gọi tắt mặt trụ tròn xoay này là mặt trụ. Đường thẳng ∆ gọi là trục, đường thẳng l là đường sinh và r là bán kính của mặt trụ đó.
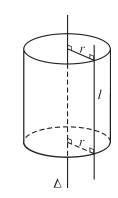
Diện tích xung quanh của hình trụ tròn xoay.
a) Một hình lăng trụ gọi là nội tiếp một hình trụ nếu hai đáy của hình lăng trụ nội tiếp hai đường tròn đáy của hình trụ. Khi đó, ta còn nói hình trụ ngoại tiếp hình lăng trụ.
- Định nghĩa: Diện tích xung quanh của hình trụ tròn xoay là giới hạn của diện tích xung quanh của hình lăng trụ đều nội tiếp hình trụ đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính diện tích xung quanh của hình trụ.
- Diện tích xung quanh của hình trụ tròn xoay bằng tích của độ dài đường tròn đáy và độ dài đường sinh:
(r là bán kính của hình trụ, l là độ dài đường sinh của hình trụ).
- Chú ý: Diện tích xung quanh, diện tích toàn phần của hình trụ tròn xoay cũng là diện tích xung quanh, diện tích toàn phần của khối trụ được giới hạn bởi hình trụ đó.
Thể tích khối trụ tròn xoay.
a) Định nghĩa: Thể tích của khối trụ tròn xoay là giới hạn của thể tích khối lăng trụ đều nội tiếp khối trụ đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính thể tích khối trụ tròn xoay.
Gọi V là thể tích của khối trụ tròn xoay có diện tích đáy B và chiều cao h, ta có công thức: V = B.h.
Như vậy, nếu bán kính đáy bằng r thì , khi đó:
3_MẶT CẦU
- Tập hợp những điểm M trong không gian cách điểm O cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm O, bán kính r.
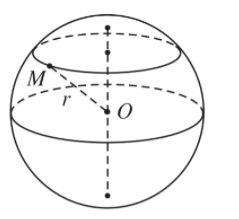
Ta kí hiệu mặt cầu tâm O, bán kính r là S(O; r) hay viết tắt là (S). Như vậy ta có mặt cầu S(O; r) = {M| OM = r}.
- Nếu hai điểm C; D nằm trên mặt cầu S(O; r) thì đoạn thẳng CD được gọi là dây cung của mặt cầu đó.
- Dây cung AB đi qua tâm O được gọi là một đường kính của mặt cầu. Khi đó, độ dài đường kính bằng 2r.
Điểm nằm trong và nằm ngoài mặt cầu. Khối cầu.
Cho mặt cầu tâm O bán kính r và A là một điểm bất kì trong không gian.
- Nếu OA = r thì ta nói điểm A nằm trên mặt cầu S(O; r).
- Nếu OA < r thì ta nói điểm A nằm trong mặt cầu S(O; r).
- Nếu OA > r thì ta nói điểm A nằm ngoài mặt cầu S(O; r).
Tập hợp các điểm thuộc mặt cầu S(O; r) cùng với các điểm nằm trong mặt cầu đó được gọi là khối cầu hoặc hình cầu tâm O, bán kính r.
Công thức tính diện tích mặt cầu và thể tích khối cầu.
- Mặt cầu bán kính r có diện tích là: .
- Khối cầu bán kính r có thể tích là: .
- Chú ý:
a) Diện tích S của mặt cầu bán kính r bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.
b) Thể tích V của khối cầu bán kính r bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Ôn tập chương 2: Mặt trụ, mặt nón, mặt cầu (mới 2024 + Bài Tập) – Toán 12
Câu 9:
18/01/2025Hãy viết 5 số thập phân ở giữa 0 và 1. Sắp xếp các số đó theo thứ tự từ bé đến lớn.
 Xem đáp án
Xem đáp án
* Lời giải:
Các số thập phân ở giữa 0 và 1 là : 0, 01; 0,02; 0,03 ; 0,04 ; 0,05;……
( hoặc có nhiều kết quả khác : 0,001 ; 0,002 ; ……..)
* Phương pháp giải:
Nắm lại kiến thức số thập phân
* Lý thuyết nắm thêm
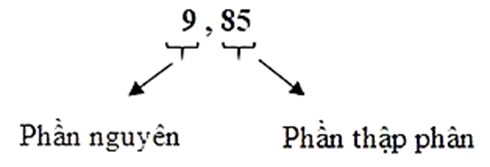
Cấu tạo số thập phân
- Mỗi số thập phân gồm hai phần: phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.
- Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
Ví dụ:
9,85 đọc là: chín phẩy tám mươi lăm
Dạng 1: Các bài toán đơn về số thập phân
1. Phương pháp giải
- Đối với dạng toán này, chúng ta thực hiện các bước giải giống như thực hiện giải bài toán có lời văn liên quan đến số tự nhiên.
- Chúng ta chỉ cần thực hiện các phép tính cộng, trừ, nhân, chia liên quan đến số thập phân để tính kết quả.
Dạng 2: Bài toán hợp về số thập phân
1. Phương pháp giải
- Đối với dạng toán này chúng ta cũng thực hiện các bước giải như giải các bài toán liên quan đến số tự nhiên.
- Tuy nhiên ta cần thực hiện nhiều bước giải hơn để tìm ra đáp án so với dạng toán đầu tiên.
Dạng 1: Cộng số thập phân
1. Phương pháp giải
- Muốn cộng hai số thập phân ta làm như sau:
+ Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
+ Cộng như cộng các số tự nhiên.
+ Viết dấu phẩy ở cột thẳng cột với các dấu phẩy của các số hạng
- Để tính tổng của nhiều số thập phân, ta làm tương tự như tính tổng của hai số thập phân.
Dạng 2: Trừ số thập phân
1. Phương pháp giải
- Muốn trừ một số thập phân cho một số thập ta làm như sau:
+ Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
+ Trừ như trừ các số tự nhiên.
+ Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
Dạng 3: Phép nhân phân số
1. Phương pháp giải
- Nhân một số thập phân với một số tự nhiên:
+ Nhân như nhân các số tự nhiên
+ Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số, rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
- Nhân một số thập với 10, 100, 1000, ... ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba,.. chữ số.
- Nhân một số thập phân với 0,1; 0,01; 0,001 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba,.. chữ số.
- Nhân một số thập phân với một số thập ta làm như sau:
+ Nhân như nhân các số tự nhiên.
+ Đếm xem trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
Xem thêm các bài viết liên quan hay, chi tiết:
50 bài tập Giải bài toán có lời văn về số thập phân lớp 5 (có đáp án 2025) và cách giải
Câu 10:
18/01/2025Hàm số nào sau đây không liên tục tại x=2?
 Xem đáp án
Xem đáp án
Đáp án đúng: C
*Lời giải:
Hàm số y=x2x−2 có tập xác định D=R\{2} nên không liên tục tại x=2.
*Phương pháp giải:
a) Hàm số đa thức liên tục trên toàn bộ tập số thực .
b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
*Một số lý thuyết liên quan:
1. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
Định nghĩa 1
Cho hàm số y = f(x) xác định trên khoảng K và x0 ∈ K.
Hàm số y = f(x) được gọi là liên tục tại x0 nếu
2. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG
Định nghĩa 2
Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.
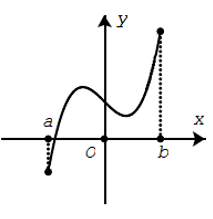
Hàm số liên tục trên khoảng (a;b)
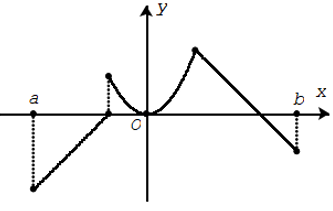
Hàm số không liên tục trên khoảng (a; b).
Định lí 2
Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x0. Khi đó:
a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x0;
b) Hàm số liên tục tại x0 nếu g(x0) ≠ 0.
Xem thêm các bài viết liên quan hay, chi tiết:
50 bài tập về Hàm số liên tục (có đáp án 2024) và cách giải
Hàm số liên tục | Lý thuyết, công thức, các dạng bài tập và cách giải
Dùng định nghĩa, xét tính liên tục của hàm số: a) f(x) = x^3 ‒ 3x + 2 tại điểm x = ‒2
Câu 11:
18/01/2025Điểm cuối của góc lượng giác α ở góc phần tư thứ mấy nếu √sin2α =sin α
 Xem đáp án
Xem đáp án
Đáp án đúng: C.
* Lời giải:
Ta có nên |sin α| = sin α
Tương đương sinα ≥ 0
Điểm cuối của góc lượng giác α nằm trong góc phần tư thứ I hoặc II
*Phương pháp giải:
- Để xác định được xem điểm cuối của góc lượng giác thuộc góc phần tư thứ mấy ta sẽ xét xem dấu của cos anpha đang < 0 hay > 0
*Một số lý thuyết và dạng bài tập về công thức lượng giác:
1. Công thức cộng lượng giác
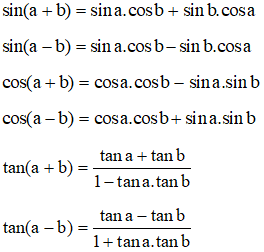
2. Công thức nhân, hạ bậc lượng giác
* Công thức nhân đôi:
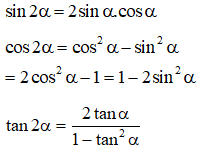
* Công thức hạ bậc:
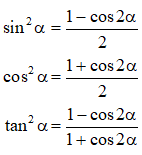
* Công thức nhân ba:
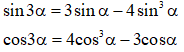
3. Công thức biến đổi tích thành tổng
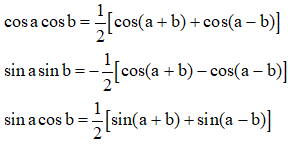
4. Công thức biển đổi tổng thành tích

5. Công thức nghiệm của phương trình lượng giác
a) Phương trình lượng giác cơ bản
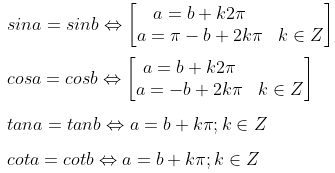
b) Phương trình lượng giác đặc biệt
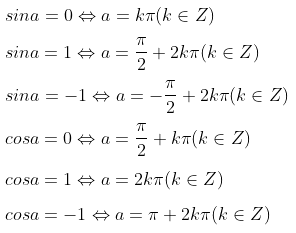
6. Bảng giá trị lương giác của các góc đặc biệt
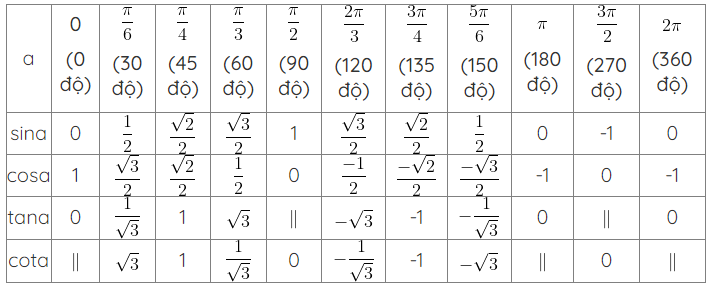
Các dạng bài tập lượng giác
Dạng 3.1: Tính giá trị lượng giác của góc đặc biệt
a. Phương pháp giải:
- Sử dụng định nghĩa giá trị lượng giá của một góc.
- Sử dụng tính chất và bảng giá trị lượng giác đặc biệt.
- Sử dụng các công thức lượng giác.
Dạng 3.2: Chứng minh đẳng thức lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Dùng hệ thức lượng giác biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
Dạng 3.3: Thu gọn biểu thức lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
Xem thêm các bài viết liên quan hay, chi tiết
Công thức lượng giác (2024) và cách giải bài tập chi tiết nhất
Câu 12:
18/01/2025Cho tập hợp L = {n| n = 2k + 1 với k ∈ N}.
a) Nêu bốn số tự nhiên thuộc tập L và hai số tự nhiên không thuộc tập L;
b) Hãy mô tả tập L bằng cách nêu dấu hiệu đặc trưng theo một cách khác.
 Xem đáp án
Xem đáp án
* Lời giải.
L = {n| n = 2k + 1 với k ∈ N }.
a)
+) Với k = 0, ta được: n = 2. 0 + 1 = 1 ∈ L
+) Với k = 1, ta được: n = 2. 1 + 1 = 3 ∈ L
+) Với k = 2, ta được: n = 2. 2 + 1 = 5 ∈ L
+) Với k = 3, ta được: n = 2. 3 + 1 = 7 ∈ L
Do đó bốn số tự nhiên thuộc tập L là: 1; 3; 5; 7
Vậy ta thấy hai số tự nhiên không thuộc tập L là: 0; 2
b)
Nhận thấy các số: 1; 3; 5; 7; ... là các số tự nhiên lẻ.
Tương tự với mọi số tự nhiên k thì ta tìm được các số n thuộc tập hợp L đều là các số tự nhiên lẻ.
Do đó ta viết có thể viết tập hợp L bằng cách nêu dấu hiệu đặc trưng khác như sau:
L = {n ∈ ℕ | n là các số lẻ}.
*Phương pháp giải
Áp dụng kiến thức về phần tập hợp để làm bài
*Một số lý thuyết nắm thêm về tập hợp:
1. Tập hợp và phần tử của tập hợp
Tập hợp là một khái niệm cơ bản của toán học (không định nghĩa).
Tập hợp được kí hiệu là các chữ cái in hoa: A, B, C, D, …
2. Mô tả một tập hợp
2.1. Liệt kê các phần tử của tập hợp
Viết tất cả các phần tử của tập hợp trong dấu {} theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.
2.2. Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp
Gọi x là phần tử của tập hợp, chỉ ra tính chất đặc trưng của phần tử và viết tập hợp đã cho.
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 13:
18/01/2025Cho tam giác ABC thoả mãn b2+c2−a2 = √3bc. Khi đó :
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải
Áp dụng định lí ciosin trong tam giác ta có:
*Phương pháp giải:
- Nắm vững công thức tính diện tích tam giác bằng lượng giác
Định lí côsin
Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:
a2 = b2 + c2 – 2bccosA,
b2 = c2 + a2 – 2cacosB,
c2 = a2 + b2 – 2abcosC.
Công thức tính diện tích tam giác:
Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:
S = bc.sinA = ca.sinB = ab.sinC
Công thức Heron:
Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:
Cho tam giác ABC có BC = a, CA = b, AB = c, . Khi đó, diện tích S của tam giác ABC là:.
Trong đó p là nửa chu vi tam giác ABC.
Tổng, hiệu và tích vô hướng của hai vectơ:
+ Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì .
+ Hai vectơ đối nhau:
Hai vecto , là hai vecto đối nhau khi và chỉ khi .
Với hai điểm A, B, ta có: .
+ Hiệu 2 vectơ:
Với ba điểm bất kì A, B, O ta có: .
+ Tích vectơ vô hướng
Với hai vecto bất kì , và hai số thực h, k, ta có:
+) k() = k + k; k() = k - k;
+) (h + k) = h + k;
+) h(k) = (hk);
+) 1 = ; (-1) = -.
+ Trung điểm của đoạn thẳng
Nếu I là trung điểm của đoạn thẳng AB thì với điểm M bất kì.
Câu 14:
18/01/2025Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;3;-4). Tính khoảng cách từ M đến trục Oy
 Xem đáp án
Xem đáp án
Đáp án đúng: C
*Lời giải:
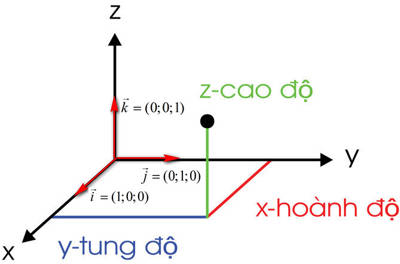
Hình chiếu vuông góc của điểm M lên trục Oy là H(0;3;0)
Khoảng cách từ M đến Oy bằng:
*Phương pháp giải:
gọi hình chiếu của M lên oy. tính khoảng cách đoạn MH
*Lý thuyết cần nắm và các dạng bài toán về phương trình mặt phẳng:
Phương trình tổng quát của mặt phẳng
1. Định nghĩa.
- Phương trình có dạng Ax + By + Cz + D = 0 trong đó A; B; C không đồng thời bằng 0 , được gọi là phương trình tổng quát của mặt phẳng.
- Nhận xét.
a) Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một vecto pháp tuyến là .
b) Phương trình mặt phẳng đi qua điểm M (x0; y0; z0) và nhận vectơ khác là vecto pháp tuyến là: A(x- x0 ) + B( y – y0) + C(z – z0) = 0.
2. Các trường hợp riêng
Trong không gian Oxyz, cho mặt phẳng (α) : Ax + By + Cz + D = 0.
a) Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.
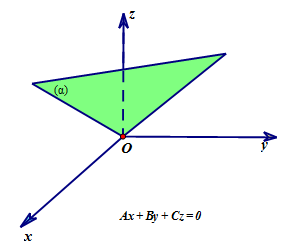
b)
- Nếu thì mặt phẳng (α) song song hoặc chứa trục Ox.
- Nếu thì mặt phẳng (α) song song hoặc chứa trục Oy.
- Nếu thì mặt phẳng (α) song song hoặc chứa trục Oz.
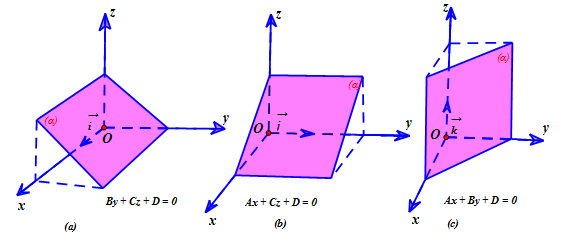
c)
- Nếu A = B = 0; thì mặt phẳng (α) song song hoặc trùng với (Oxy).
- Nếu A = C = 0; thì mặt phẳng (α) song song hoặc trùng với (Oxz).
- Nếu B = C = 0; thì mặt phẳng (α) song song hoặc trùng với (Oyz).
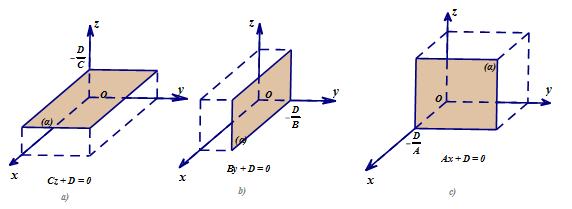
Phương trình mặt phẳng theo đoạn chắn . Ở đây (α) cắt các trục tọa độ tại các điểm (a; 0; 0); (0; b; 0); (0; 0; c) với .
Điều kiện để hai mặt phẳng song song, vuông góc.
Trong không gian Oxyz, cho hai mặt phẳng (α) và (β) có phương trình:
(α): A1x + B1y + C1z + D1 = 0
(β): A2x + B2y + C2z + D2 = 0
Hai mặt phẳng (α); (β) có hai vecto pháp tuyến lần lượt là:
1. Điều kiện để hai mặt phẳng song song.
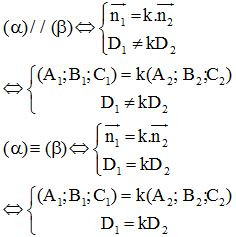
- Chú ý: Để (α) cắt (β)
2. Điều kiện để hai mặt phẳng vuông góc.
Khoảng cách từ một điểm đến một mặt phẳng.
- Định lí: Trong không gian Oxyz, cho điểm M0(x0; y0; z0) và mặt phẳng (α): Ax + By + Cz + D = 0 .
Khi đó khoảng cách từ điểm M0 đến mặt phẳng (α) được tính:
Dạng 1: Xác định vectơ pháp tuyến của mặt phẳng
Phương pháp giải:
Cho mặt phẳng có phương trình Ax + By + Cz + D = 0.
Khi đó mặt phẳng có một VTPT là .
Dạng 2: Viết phương trình mặt phẳng khi đã biết một điểm đi qua và vectơ pháp tuyến
Phương pháp giải:
Cho mặt phẳng đi qua điểm và nhận vectơ làm vectơ pháp tuyến. Khi đó phương trình mặt phẳng là:
Dạng 3: Viết phương trình mặt phẳng đi qua điểm M và song song với mặt phẳng (P) cho trước.
Phương pháp giải:
+) Mặt phẳng song song với mặt phẳng (P) cho trước nên vectơ pháp tuyến của mặt phẳng chính là vectơ pháp tuyến của mặt phẳng (P).
+) Từ đó viết phương trình mặt phẳng đi qua M và có vectơ pháp tuyến là .
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Phương trình mặt phẳng (mới 2024 + Bài Tập) – Toán 12
50 bài toán về phương trình mặt phẳng (có đáp án 2024) – Toán 12
Câu 15:
18/01/2025Trong không gian Oxyz, góc giữa hai mặt phẳng (Oxy) và (Oyz)bằng
 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải:
Ta có vectơ pháp tuyến của và lần lượt là và .
Vì nên .
*Phương pháp giải:
Để tính góc giữa hai mặt phẳng (α) và (β) ta có thể thực hiện theo một trong các cách sau:
Cách 1. Tìm hai đường thẳng a; b lần lượt vuông góc với hai mặt phẳng (α) và (β). Khi đó góc giữa hai đường thẳng a và b chính là góc giữa hai mặt phẳng (α) và (β).
Cách 2. Sử dụng công thức hình chiếu: Gọi S là diện tích của hình (H) trong mp(α) và S’ là diện tích hình chiếu (H’) của (H) trên mp(β) thì S’ = S.cosφ
⇒ cosα ⇒ φ
Cách 3. Xác định cụ thể góc giữa hai mặt phẳng rồi sử dụng hệ thức lượng trong tam giác để tính.
+ Bước 1: Tìm giao tuyến Δ của hai mp
+ Bước 2: Chọn mặt phẳng (γ) vuông góc Δ
+ Bước 3: Tìm các giao tuyến (γ) với (α); (β)
⇒ ((α), (β)) = (a, b)
*Cách giải và các dạng bài toán về
1. Góc giữa 2 mặt phẳng là gì?
- Khái niệm: Góc giữa 2 mặt phẳng là góc được tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
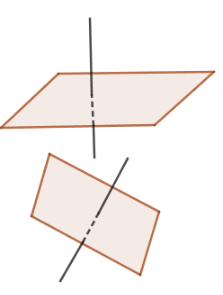
Trong không gian 3 chiều, góc giữa 2 mặt phẳng còn được gọi là ‘góc khối’, là phần không gian bị giới hạn bởi 2 mặt phẳng. Góc giữa 2 mặt phẳng được đo bằng góc giữa 2 đường thẳng trên mặt 2 phẳng có cùng trực giao với giao tuyến của 2 mặt phẳng.
2. Tính chất của góc giữa 2 mặt phẳng
Từ định nghĩa trên ta có:
- Góc giữa 2 mặt phẳng song song bằng 0 độ,
- Góc giữa 2 mặt phẳng trùng nhau bằng 0 độ.
3. Cách xác định góc giữa 2 mặt phẳng
Gọi P là mặt phẳng 1, Q là mặt phẳng 2
Trường hợp 1: Hai mặt phẳng (P), (Q) song song hoặc trùng nhau thì góc của 2 mặt phẳng bằng 0,
Trường hợp 2: Hai mặt phẳng (P), (Q) không song song hoặc trùng nhau.
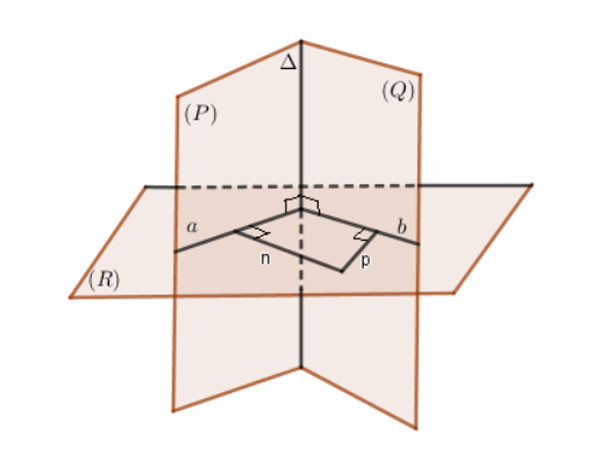
Cách 1: Dựng 2 đường thẳng n và p vuông góc lần lượt với 2 mặt phẳng (P), (Q). Khi đó góc giữa 2 mặt phẳng (P), (Q) là góc giữa 2 đường thẳng n và p.
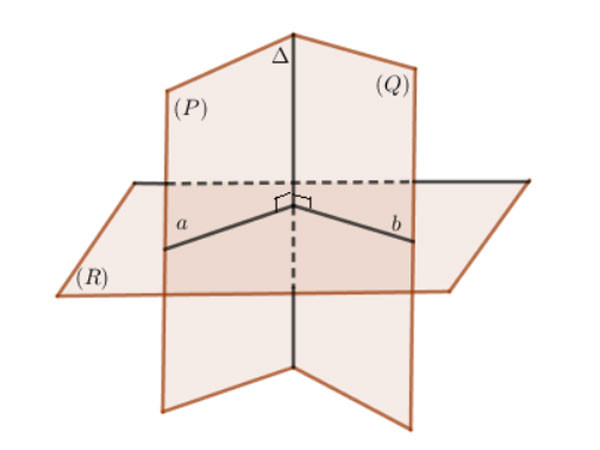
Cách 2: Để xác định góc giữa 2 mặt phẳng đầu tiên bạn cần xác định giao tuyến ∆ của 2 mặt phẳng (P) và (Q). Tiếp theo, bạn tìm một mặt phẳng (R) vuông góc với giao tuyến Δ của 2 mặt phẳng (P), (Q) và cắt 2 mặt phẳng tại các giao tuyến a, b.
⇒ Góc giữa 2 mặt phẳng (P), (Q) là góc giữa a và b.
Xem thêm các bài viết liên quan hay, chi tiết
Góc giữa hai mặt phẳng (lý thuyết, công thức) các dạng bài tập và cách giải
Câu 16:
18/01/2025tổng số mặt và số cạnh của hình chóp ngũ giác
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải
Hình chóp ngũ giác có 6 mặt và 10 cạnh.
*Phương pháp giải
Hình chóp ngũ giác có 6 mặt và 10 cạnh.
*Lý thuyến cần nắm về hình chóp đều, hình chóp cụt đều:
Hình chóp đều
Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh (là đỉnh của hình chóp).
+ Chân đường cao của hình chóp đều là tâm của đường tròn đi qua các đỉnh của mặt đáy.
+ Đường cao vẽ từ đỉnh của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
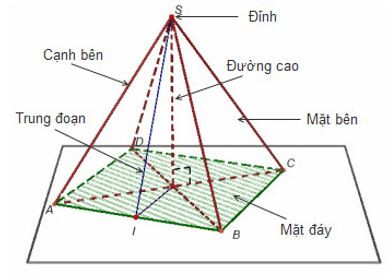
Hình chóp cụt đều
- Cắt hình chóp đều bởi một mặt phẳng song song với đáy. Phần hình chóp nằm giữa mặt phẳng đó và mặt đáy của hình chóp gọi là hình chóp cụt đều.
- Nhận xét: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
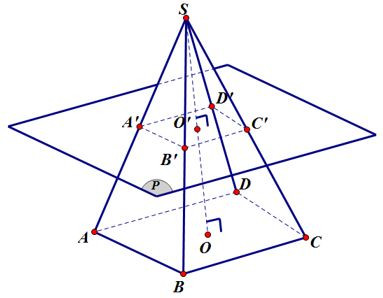
Hình trên có hình chóp cụt đều là ABCD.A’B’C’D’.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hình chóp đều và hình chóp cụt đều (mới + Bài Tập) – Toán 8
Toán 8 Bài 7 giải vở bài tập: Hình chóp đều và hình chóp cụt đều
50 Bài tập Hình chóp đều và hình chóp cụt đều Toán 8 mới nhất
Câu 17:
18/01/2025Tính thể tích khối tứ diện đều cạnh a.
 Xem đáp án
Xem đáp án
*Lời giải
Gọi ABCD là tứ diện đều cạnh a.
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD
⇒ HB = HC = HD nên H nằm trên trục đường tròn ngoại tiếp tam giác BCD. (1)
Lại có: AB = AC = AD vì ABCD là tứ diện đều
⇒ HA là trục đường tròn ngoại tiếp tam giác BCD
⇒ HA ⊥ (BCD)
Vì tam giác BCD là tam giác đều nên H đồng thời trọng tâm tam giác BCD. Gọi M là trung điểm của CD.
Xét tam giác BCD ta có:
Áp dụng định lí pytago vào tam giác vuông AHB ta được:
Diện tích tam giác đều BCD cạnh a là:
Do đó, thể tích khối tứ diện đều ABCD là:
*Phương pháp giải
Áp dụng công thức tính Thể tích khối chóp là: V = 1/3. S.h
*Lý thuyến cần nắm về khối đa diện và thể tích khối đa diện
Người ta chứng minh được rằng: có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất V(H) thỏa mãn các tính chất sau:
a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.
b) Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2).
c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì:
V(H) = V(H1) + V(H2).
Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Số đó cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).
Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.
- Định lí : Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.
II. Thể tích của khối lăng trụ.
Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
III. Thể tích khối chóp.
Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là:
.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Khái niệm về khối đa diện (mới 2024 + Bài Tập) – Toán 12
50 bài toán về thể tích khối đa diện (có đáp án 2024) – Toán 12
Câu 18:
18/01/2025Tính thể tích V của khối hộp đứng có đáy là hình vuông cạnh a và độ dài cạnh bên bằng √2a.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
* Lời giải
Ta có V=B.h=a2.√2a=√2a3.
* Phương pháp giải
- Nắm lại kiến thức về hình hộp đứng: V =B..h
*Một số lý thuyết cần nắm về hình hộp chữ nhật:
a) Hình hộp chữ nhật
Định nghĩa: Hình hộp chữ nhật là hình không gian có 6 mặt đều là những hình chữ nhật.
+ Hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh.
+ Hai mặt đối diện nhau được xem là mặt đáy của hình hộp chữ nhật, các mặt còn lại được gọi là mặt bên

+ Hình lập phương là hình hộp chữ nhật có 6 mặt đều là những hình vuông.

b) Mặt phẳng và đường thẳng
+ Qua ba điểm không thẳng hàng xác định một và chỉ một mặt phẳng.
+ Qua hai đường thẳng cắt nhau xác định một và chỉ một mặt phẳng.
+ Đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đó đều thuộc mặt phẳng.
c) Hai đường thẳng song song trong không gian:
+ Hai đường thẳng a, b gọi là song song với nhau nếu chúng cùng nằm trong một mặt phẳng và không có điểm chung. Kí hiệu a // b.
+ Hai đường thẳng phân biệt, cùng song song với một đường thẳng thứ ba thì song song với nhau.
Chú ý: Hai đường thẳng phân biệt trong không gian có thể:
– Cắt nhau – Song song – Chéo nhau (không cùng nằm trong một mặt phẳng)
Xem thêm các bài viết liên quan hay, chi tiết
Trắc nghiệm Hình hộp chữ nhật có đáp án (Nhận biết)
Câu 19:
19/01/2025Tính sin2a, cos2a, tan2a biết
 Xem đáp án
Xem đáp án
*Lời giải:
*Phương pháp giải:
- dùng các công thức lượng giác biến đổi 2 vế của phương trình, giải và tìm ra nghiệm
*Lý thuyết và các dạng bài tập về phương trình lượng giác cơ bản:
Phương trình cosx=a
- Trường hợp |a| > 1
Phương trình cosx = a vô nghiệm vì với mọi x.
- Trường hợp .
Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là:
Phương trình tanx=a
- Điều kiện xác định của phương trình là
Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là:
+) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là:
Tổng quát; tan f(x) = tan g(x) .
+) Phương trình tanx = tanβ0 có các nghiệm là: .
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết
*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:
at + b = 0 (1)
Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.
- Phương pháp:
Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.
Phương trình bậc hai với hàm số lượng giác
Định nghĩa.
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:
at2 + bt + c = 0
Trong đó a; b; c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Phương trình lượng giác cơ bản – Toán 11
Bài tập Phương trình lượng giác cơ bản Toán 11
Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án)– Toán 11
Câu 20:
19/01/2025Giải các phương trình tanx.tan2x = - 1
 Xem đáp án
Xem đáp án
*Lời giải:
Điều kiện của phương trình: cos x ≠ 0 và cos2x ≠ 0
tanx. tan2x = -1
sinx. sin2x = -cosx. cos2x
cos2x. cosx + sin2x. sinx = 0
cosx = 0
Kết hợp với điều kiện ta thấy phương trình vô nghiệm.
*Phương pháp giải:
- dùng các công thức lượng giác biến đổi 2 vế của phương trình, giải và tìm ra nghiệm
*Lý thuyết và các dạng bài tập về phương trình lượng giác cơ bản:
Phương trình cosx=a
- Trường hợp |a| > 1
Phương trình cosx = a vô nghiệm vì với mọi x.
- Trường hợp .
Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là:
Phương trình tanx=a
- Điều kiện xác định của phương trình là
Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là:
+) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là:
Tổng quát; tan f(x) = tan g(x) .
+) Phương trình tanx = tanβ0 có các nghiệm là: .
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết
*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:
at + b = 0 (1)
Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.
- Phương pháp:
Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.
Phương trình bậc hai với hàm số lượng giác
Định nghĩa.
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:
at2 + bt + c = 0
Trong đó a; b; c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Phương trình lượng giác cơ bản – Toán 11
Bài tập Phương trình lượng giác cơ bản Toán 11
Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án)– Toán 11
Câu 21:
19/01/2025Với góc α bất kì. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: C
Lời giải:
Ta có:
sin2α+cos2(1800−α)=sin2α+(−cosα)2=sin2α+cos2α=1
*Phương pháp giải:*Phương pháp giải:
*Phương pháp giải:
Sử dụng giá trị lượng giác của các góc có liên quan đặc biệt và sin2α+cos2α=1∀α.
*Lý thuyết và các dạng bài tập về phương trình lượng giác cơ bản:
Phương trình cosx=a
- Trường hợp |a| > 1
Phương trình cosx = a vô nghiệm vì với mọi x.
- Trường hợp .
Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là:
Phương trình tanx=a
- Điều kiện xác định của phương trình là
Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là:
+) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là:
Tổng quát; tan f(x) = tan g(x) .
+) Phương trình tanx = tanβ0 có các nghiệm là: .
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết
*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:
at + b = 0 (1)
Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.
- Phương pháp:
Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.
Phương trình bậc hai với hàm số lượng giác
Định nghĩa.
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:
at2 + bt + c = 0
Trong đó a; b; c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Phương trình lượng giác cơ bản – Toán 11
Bài tập Phương trình lượng giác cơ bản Toán 11
Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án)– Toán 11
Câu 22:
19/01/2025Tổng các góc của tất cả các mặt khối của đa diện đều loại {4;3} là
 Xem đáp án
Xem đáp án
Đáp án đúng: C.
*Lời giải:
Khối đa diện đều loại {4; 3} là khối lập phương, gồm 6 mặt, mỗi mặt đều là hình vuông.
Tổng các góc của hình vuông là 360o hay 2π.
Vậy tổng tất cả các góc của khối đa diện đều loại {4; 3} là 6 . 2π = 12π.
*Phương pháp giải
Dựa vào lí thuyết hoặc bảng dưới đây

*Lý thuyết nắm thêm về khối đa diện đều:

Chú ý. Gọi Đ là tổng số đỉnh, C là tổng số cạnh và M là tổng các mặt của khối đa diện đều loại {n; p}. Ta có pĐ = 2C = nM
- Xét tứ diện đều
- Xét khối lập phương
- Xét bát diện đều
- Xét khối mười hai mặt đều
- Xét khối hai mươi mặt đều
*) Các dạng bài về khối đa diện:
a) Nhận diện khối đa diện
b) Tính thể tích khối chóp có cạnh bên vuông góc với đáy
+ Một hình chóp có một cạnh bên vuông góc với đáy thì cạnh bên đó chính là đường cao.
+ Một hình chóp có hai mặt bên kề nhau cùng vuông góc với đáy thì cạnh bên là giao tuyến của hai mặt đó vuông góc với đáy
c) Tính thể tích khối lăng trụ đứng, lăng trụ đều
+) Khối lăng trụ đứng
Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.
Tính chất:
+ Các mặt bên hình lăng trụ đứng là hình chữ nhật
+ Các mặt bên hình lăng trụ đứng vuông góc với mặt đáy
+ Chiều cao là cạnh bên
+) Khối lăng trụ đều
Định nghĩa: Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều
Tính chất:
+ Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau
+ Chiều cao là cạnh bên.
Xem thêm một số bài viết liên quan hay, chi tiết:
Câu 23:
19/01/2025Tính đường kính mặt cầu ngoại tiếp hình lập phương có cạnh bằng a√3.
 Xem đáp án
Xem đáp án
Đáp án đúng: A
* Lời giải:
* Phương pháp giải:
Tính đường kính mặt cầu chính là đường chéo hình lập phương
*Một số lý thuyết và dạng bài tập về mặt cầu, mặt nón, mặt trụ:
1_MẶT NÓN:
Hình nón tròn xoay và khối nón tròn xoay.
a) Cho tam giác OIM vuông tại I. Khi quay tam giác đó xung quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.

Hình tròn tâm I sinh bởi các điểm thuộc cạnh IM khi quay quanh trục OI được gọi là mặt đáy của hình nón, điểm O được gọi là đỉnh của hình nón.
Độ dài đoạn OI gọi là chiều cao của hình nón, đó cũng chính là khoảng cách từ O đến mặt phẳng đáy. Độ dài đoạn OM gọi là độ dài đường sinh của hình nón.
Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh OM khi quay quanh OI được gọi là mặt xung quanh của hình nón đó.
Diện tích xung quanh của hình nón tròn xoay.
a) Một hình chóp được gọi là nội tiếp một hình nón nếu đáy của hình chóp là đa giác nội tiếp đường tròn đáy của hình nón và đỉnh của hình chóp là đỉnh của hình nón. Khi đó, ta còn nói hình nón ngoại tiếp hình chóp.
a_Định nghĩa: Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.
Công thức tính diện tích xung quanh của hình nón.
- Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh.
(r là bán kính đường tròn đáy, l là độ dài đường sinh).
- Người ta gọi tổng của diện tích xung quanh và diện tích đáy là diện tích toàn phần của hình nón.
- Chú ý: Diện tích xung quanh, diện tích toàn phần của hình nón tròn xoay cũng là diện tích xung quanh , diện tích toàn phần của khối nón được giới hạn bởi hình nón đó.
Thể tích khối nón tròn xoay.
a) Định nghĩa.
Thể tích của khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính thể tích khối nón tròn xoay.
Gọi V là thể tích của khối nón tròn xoay có diện tích đáy B và chiều cao h, ta có công thức:
Như vậy, nếu bán kính đáy bằng r thì , khi đó: .
2_MẶT TRỤ
a) Định nghĩa
Trong mặt phẳng (P) cho hai đường thẳng ∆ và l song song với nhau, cách nhau một khoảng bằng r. Khi quay mặt phẳng (P) xung quanh ∆ thì đường thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay.
Người ta thường gọi tắt mặt trụ tròn xoay này là mặt trụ. Đường thẳng ∆ gọi là trục, đường thẳng l là đường sinh và r là bán kính của mặt trụ đó.

Diện tích xung quanh của hình trụ tròn xoay.
a) Một hình lăng trụ gọi là nội tiếp một hình trụ nếu hai đáy của hình lăng trụ nội tiếp hai đường tròn đáy của hình trụ. Khi đó, ta còn nói hình trụ ngoại tiếp hình lăng trụ.
- Định nghĩa: Diện tích xung quanh của hình trụ tròn xoay là giới hạn của diện tích xung quanh của hình lăng trụ đều nội tiếp hình trụ đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính diện tích xung quanh của hình trụ.
- Diện tích xung quanh của hình trụ tròn xoay bằng tích của độ dài đường tròn đáy và độ dài đường sinh:
(r là bán kính của hình trụ, l là độ dài đường sinh của hình trụ).
- Chú ý: Diện tích xung quanh, diện tích toàn phần của hình trụ tròn xoay cũng là diện tích xung quanh, diện tích toàn phần của khối trụ được giới hạn bởi hình trụ đó.
Thể tích khối trụ tròn xoay.
a) Định nghĩa: Thể tích của khối trụ tròn xoay là giới hạn của thể tích khối lăng trụ đều nội tiếp khối trụ đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính thể tích khối trụ tròn xoay.
Gọi V là thể tích của khối trụ tròn xoay có diện tích đáy B và chiều cao h, ta có công thức: V = B.h.
Như vậy, nếu bán kính đáy bằng r thì , khi đó:
3_MẶT CẦU
- Tập hợp những điểm M trong không gian cách điểm O cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm O, bán kính r.

Ta kí hiệu mặt cầu tâm O, bán kính r là S(O; r) hay viết tắt là (S). Như vậy ta có mặt cầu S(O; r) = {M| OM = r}.
- Nếu hai điểm C; D nằm trên mặt cầu S(O; r) thì đoạn thẳng CD được gọi là dây cung của mặt cầu đó.
- Dây cung AB đi qua tâm O được gọi là một đường kính của mặt cầu. Khi đó, độ dài đường kính bằng 2r.
Điểm nằm trong và nằm ngoài mặt cầu. Khối cầu.
Cho mặt cầu tâm O bán kính r và A là một điểm bất kì trong không gian.
- Nếu OA = r thì ta nói điểm A nằm trên mặt cầu S(O; r).
- Nếu OA < r thì ta nói điểm A nằm trong mặt cầu S(O; r).
- Nếu OA > r thì ta nói điểm A nằm ngoài mặt cầu S(O; r).
Tập hợp các điểm thuộc mặt cầu S(O; r) cùng với các điểm nằm trong mặt cầu đó được gọi là khối cầu hoặc hình cầu tâm O, bán kính r.
Công thức tính diện tích mặt cầu và thể tích khối cầu.
- Mặt cầu bán kính r có diện tích là: .
- Khối cầu bán kính r có thể tích là: .
- Chú ý:
a) Diện tích S của mặt cầu bán kính r bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.
b) Thể tích V của khối cầu bán kính r bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Ôn tập chương 2: Mặt trụ, mặt nón, mặt cầu (mới 2024 + Bài Tập) – Toán 12
Câu 24:
19/01/2025Có biễu diễn “0000 0000 0010 0101” (dùng mã bù 2, có dấu), giá trị của chúng là:
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải:
Có biễu diễn “0000 0000 0010 0101” (dùng mã bù 2, có dấu), giá trị của chúng là 37
*Phương pháp giải
Có biễu diễn “0000 0000 0010 0101” (dùng mã bù 2, có dấu), giá trị của chúng là 37
*Lý thuyết nắm thêm
a) Cơ sở dữ liệu tập trung
- Một CSDL tập trung được lưu trữ trên một máy tính (Hình 1).
- Việc quản lí, cập nhật được thực hiện tại chính vị trí này.
- Người dùng có thể truy cập và khai thác thông tin bằng chính máy tính chứa CSDL hay thông qua kết nối mạng.
- Ưu điểm của hệ CSDL tập trung: truy cập và điều phối dữ liệu dễ dàng hơn, phù hợp cho các cơ quan, doanh nghiệp, tổ chức.
- Ví dụ: Hệ thống quản lí học sinh của trường và hệ thống bán vé tàu hoả của Tổng công ty Đường sắt Việt Nam.
- Hạn chế của hệ CSDL tập trung: khi gặp sự cố, các chương trình ứng dụng không thể chạy được.
- CSDL phân tán là tập hợp dữ liệu được lưu trữ trên nhiều máy tính khác nhau trong một mạng máy tính.
- Mỗi máy tính có CSDL cục bộ và thực hiện ít nhất một ứng dụng cục bộ.
- Mỗi máy tính phải tham gia ít nhất một ứng dụng toàn cục sử dụng CSDL của ít nhất hai trạm khác.
- Mỗi hệ CSDL gồm 3 lớp: CSDL, hệ quản trị CSDL và ứng dụng CSDL.
- Kiến trúc hệ CSDL có thể phân chia thành các thành phần chức năng để hiểu và chỉnh sửa một cách độc lập.
a) Kiến trúc phổ biến của hệ CSDL tập trung
- Hệ CSDL tập trung theo kiến trúc khách-chủ (Client-Server).
- Hệ quản trị CSDL bao gồm thành phần yêu cầu tài nguyên và cung cấp tài nguyên.
- Thành phần cung cấp tài nguyên được đặt trên máy chủ.
- Thành phần yêu cầu tài nguyên có thể được cài đặt trên nhiều máy khác trên mạng, được gọi là máy khách.
Xem thêm một số bài viết liên quan hay, chi tiết:
Lý thuyết Tin học 11 (Cánh diều) Bài 7: Các loại kiến trúc của hệ cơ sở dữ liệu
Câu 25:
19/01/2025 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải:
Có biểu diễn “1100 1000” đối với số nguyên có dấu, 8 bit, dùng phương pháp “Mã bù 2”, giá trị của nó là -56
*Phương pháp giải
Có biểu diễn “1100 1000” đối với số nguyên có dấu, 8 bit, dùng phương pháp “Mã bù 2”, giá trị của nó là -56
*Lý thuyết nắm thêm
a) Cơ sở dữ liệu tập trung
- Một CSDL tập trung được lưu trữ trên một máy tính (Hình 1).
- Việc quản lí, cập nhật được thực hiện tại chính vị trí này.
- Người dùng có thể truy cập và khai thác thông tin bằng chính máy tính chứa CSDL hay thông qua kết nối mạng.
- Ưu điểm của hệ CSDL tập trung: truy cập và điều phối dữ liệu dễ dàng hơn, phù hợp cho các cơ quan, doanh nghiệp, tổ chức.
- Ví dụ: Hệ thống quản lí học sinh của trường và hệ thống bán vé tàu hoả của Tổng công ty Đường sắt Việt Nam.
- Hạn chế của hệ CSDL tập trung: khi gặp sự cố, các chương trình ứng dụng không thể chạy được.
- CSDL phân tán là tập hợp dữ liệu được lưu trữ trên nhiều máy tính khác nhau trong một mạng máy tính.
- Mỗi máy tính có CSDL cục bộ và thực hiện ít nhất một ứng dụng cục bộ.
- Mỗi máy tính phải tham gia ít nhất một ứng dụng toàn cục sử dụng CSDL của ít nhất hai trạm khác.
- Mỗi hệ CSDL gồm 3 lớp: CSDL, hệ quản trị CSDL và ứng dụng CSDL.
- Kiến trúc hệ CSDL có thể phân chia thành các thành phần chức năng để hiểu và chỉnh sửa một cách độc lập.
a) Kiến trúc phổ biến của hệ CSDL tập trung
- Hệ CSDL tập trung theo kiến trúc khách-chủ (Client-Server).
- Hệ quản trị CSDL bao gồm thành phần yêu cầu tài nguyên và cung cấp tài nguyên.
- Thành phần cung cấp tài nguyên được đặt trên máy chủ.
- Thành phần yêu cầu tài nguyên có thể được cài đặt trên nhiều máy khác trên mạng, được gọi là máy khách.
Xem thêm một số bài viết liên quan hay, chi tiết:
Lý thuyết Tin học 11 (Cánh diều) Bài 7: Các loại kiến trúc của hệ cơ sở dữ liệu
Câu 26:
19/01/2025Có biểu diễn “1110 0010” đối với số nguyên có dấu, 8 bit, dùng phương pháp “Dấu và độ lớn”, giá trị của nó là:
 Xem đáp án
Xem đáp án
Đáp án đúng: C
*Lời giải:
Có biểu diễn “1110 0010” đối với số nguyên có dấu, 8 bit, dùng phương pháp “Dấu và độ lớn”, giá trị của nó là -30
*Phương pháp giải
Có biểu diễn “1110 0010” đối với số nguyên có dấu, 8 bit, dùng phương pháp “Dấu và độ lớn”, giá trị của nó là -30
*Lý thuyết nắm thêm
a) Cơ sở dữ liệu tập trung
- Một CSDL tập trung được lưu trữ trên một máy tính (Hình 1).
- Việc quản lí, cập nhật được thực hiện tại chính vị trí này.
- Người dùng có thể truy cập và khai thác thông tin bằng chính máy tính chứa CSDL hay thông qua kết nối mạng.
- Ưu điểm của hệ CSDL tập trung: truy cập và điều phối dữ liệu dễ dàng hơn, phù hợp cho các cơ quan, doanh nghiệp, tổ chức.
- Ví dụ: Hệ thống quản lí học sinh của trường và hệ thống bán vé tàu hoả của Tổng công ty Đường sắt Việt Nam.
- Hạn chế của hệ CSDL tập trung: khi gặp sự cố, các chương trình ứng dụng không thể chạy được.
- CSDL phân tán là tập hợp dữ liệu được lưu trữ trên nhiều máy tính khác nhau trong một mạng máy tính.
- Mỗi máy tính có CSDL cục bộ và thực hiện ít nhất một ứng dụng cục bộ.
- Mỗi máy tính phải tham gia ít nhất một ứng dụng toàn cục sử dụng CSDL của ít nhất hai trạm khác.
- Mỗi hệ CSDL gồm 3 lớp: CSDL, hệ quản trị CSDL và ứng dụng CSDL.
- Kiến trúc hệ CSDL có thể phân chia thành các thành phần chức năng để hiểu và chỉnh sửa một cách độc lập.
a) Kiến trúc phổ biến của hệ CSDL tập trung
- Hệ CSDL tập trung theo kiến trúc khách-chủ (Client-Server).
- Hệ quản trị CSDL bao gồm thành phần yêu cầu tài nguyên và cung cấp tài nguyên.
- Thành phần cung cấp tài nguyên được đặt trên máy chủ.
- Thành phần yêu cầu tài nguyên có thể được cài đặt trên nhiều máy khác trên mạng, được gọi là máy khách.
Xem thêm một số bài viết liên quan hay, chi tiết:
Lý thuyết Tin học 11 (Cánh diều) Bài 7: Các loại kiến trúc của hệ cơ sở dữ liệu
Câu 27:
19/01/2025Điều kiện cần và đủ để số tự nhiên n chia hết cho 2 và 3 là số tự nhiên đó chia hết cho 12
 Xem đáp án
Xem đáp án
*Lời giải:
Mệnh đề này đúng là bởi vì 12 là bội chung của cả 2 và 3
cho nên khi n chia hết cho 12 thì chắc chắn n sẽ chia hết cho 2 và 3
*Phương pháp giải:
- Áp dụng dấu hiệu chia hết cho 3, 2
*Lý thuyết cần nắm và dạng bài toán về dấu hiệu chia hết cho 3:
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
Các số có tổng các chữ số không chia hết cho 3 thì không chia hết cho 3.
CÁC DẠNG TOÁN
Dạng 1: Kiểm tra một số đã cho có chia hết cho 3 hay không
Phương pháp:
Bước 1: Tính tổng các chữ số của số đã cho.
Bước 2: Kết luận:
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
Các số có tổng các chữ số không chia hết cho 3 thì không chia hết cho 3.
Dạng 2: Tìm các số chia hết cho 3 và 9
Phương pháp:
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
Những số nào chia hết cho 9 thì chia hết cho 3.
Dạng 3: Tìm các số thỏa mãn yêu cầu cho trước
Phương pháp:
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
Các số có tổng các chữ số không chia hết cho 3 thì không chia hết cho 3.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Dấu hiệu chia hết cho 3 (mới 2024 + Bài Tập) - Toán lớp 4
Câu 28:
19/01/2025Cho hàm số y=(m−1)x4−3mx2+5 . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải
[Phương pháp tự luận]
(*)
TH1 : Nếu m = 1 , (*) trở thành : hay x= 0 ,
Vậy m = 1 hàm số đạt cực đại tại x = 0
TH2 : Nếu m ≠ 1
Hàm số có cực đại mà ko có cực tiểu
Kết hợp 2 trường hợp :
*Phương pháp giải:
Tính y'
Tìm nghiệm y' thay nghiệm vào y tìm CĐ CT
*Lý thuyết cần nắm và các dạng bài tập về cực trị hàm số:
- Định nghĩa.
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là ; b là ) và điểm x0(a; b).
a) Nếu tồn tại số h > 0 sao cho f(x) < f(x0) với mọi x(x0 – h; x0 + h) và thì ta nói hàm số f(x) đạt cực đại tại x0.
b) Nếu tồn tại số h > 0 sao cho f(x) > f(x0) với mọi x(x0 – h; x0 + h) và thì ta nói hàm số f(x) đạt cực tiểu tại x0.
Điều kiện đủ để hàm số có cực trị
- Định lí 1
Giả sử hàm số y = f(x) liên tục trên khoảng K = (x0 – h; x0 + h) và có đạo hàm trên K hoặc trên K \ {x0}; với h > 0.
a) Nếu f’(x) > 0 trên khoảng (x0 – h; x0) và f’(x) < 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
b) Nếu f’(x) < 0 trên khoảng (x0 – h; x0) và f’(x) > 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực tiểu của hàm số f(x).
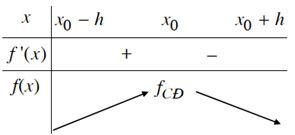
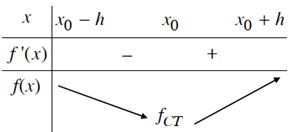
Quy tắc tìm cực trị.
- Quy tắc 1.
1. Tìm tập xác định.
2. Tính f’(x). Tìm các điểm tại đó f’(x) bằng 0 hoặc f’(x) không xác định.
3. Lập bảng biến thiên.
4. Từ bảng biến thiên suy ra các điểm cực trị.
- Định lí 2.
Giả sử hàm số y = f(x) có đạo hàm cấp hai trong khoảng (x0 – h; x0 + h) với h > 0. Khi đó:
a) Nếu f’(x0) = 0; f”(x0) > 0 thì x0 là điểm cực tiểu;
b) Nếu f’(x0) = 0; f”(x0) < 0 thì x0 là điểm cực đại.
- Quy tắc II.
1. Tìm tập xác định
2. Tính f’(x). Giải phương trình f’(x) = 0 và kí hiệu xi ( i = 1; 2; ….; n) là các nghiệm của nó.
3. Tính f”(x) và f”(xi).
4. Dựa vào dấu của f”(xi) suy ra tính chất cực trị của điểm xi.
Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba ().
- Ta có
Đồ thị hàm số có 2 điểm cực trị khi phương trình y' = 0 có hai nghiệm phân biệt .
Và không có cực trị ⇔Δ’ = b2 − 3ac ≤ 0
- Cho hàm số có hai điểm cực trị phân biệt là A, B . Khi đó:
Phương trình đường thẳng AB : y = (c - )x + (d -)
Độ dài đoạn thẳng AB = với e =
Hoặc khi đó đường thẳng qua hai điểm cực trị liên quan tới: (CASIO hỗ trợ).
Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.
Cho hàm số: () có đồ thị là (C) .
Ta có
(C) có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt hay ab < 0
Hàm số có 3 cực trị là:
.
Độ dài các đoạn thẳng:
CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1. Tìm các điểm cực trị của hàm số.
Quy tắc 1: Áp dụng định lý 2
- Tìm f’(x)
- Tìm các điểm xi (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm
- Xét dấu của f’(x). Nếu f’(x) đổi dấu khi x qua điểm xo thì hàm số có cực trị tại điểm xo
Quy tắc 2: Áp dụng định lý 3
- Tìm f’(x)
- Tìm các nghiệm xi (i = 1, 2, 3,…) của phương trình f ‘(x) = 0
- Với mỗi xi tính f ”(xi)
- Nếu f ”(xi) < 0 thì hàm số đạt cực đại tại điểm xi
- Nếu f ”(xi) > 0 thì hàm số đạt cực tiểu tại điểm xi
Dạng 2: Tìm điều kiện để hàm số có cực trị.
Sử dụng định lí 2 và định lí 3
a, Cực trị của hàm số bậc ba:
Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y’ = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ’y’ = b2 – 3ac
- Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
→ Hàm số bậc 3 không có cực trị ⇔ b2 – 3ac ≤ 0
- Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
→ Hàm số bậc 3 có 2 cực trị ⇔ b2 – 3ac > 0
b, Cực trị của hàm số bậc bốn trùng phương:
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
y' = 4ax3 + 2bx; y' = 0
⇔
- Nếu (C)có một điểm cực trị thì y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.
- Nếu (C)có ba điểm cực trị thì y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Chú ý
* Hàm số f (xác định trên D) có cực trị ⇔ ∃ xo ∈ D thỏa mãn hai điều kiện sau:
- Tại đạo hàm của hàm số tại xo phải bằng 0 hoặc hàm số không có đạo hàm tại xo
- f ‘(x) phải đổi dấu qua điểm xo hoặc f ”(xo) ≠ 0.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12
Cực trị của hàm số và cách giải các dạng bài tập (2024) mới nhất
Câu 29:
19/01/2025Tìm tất cả các giá trị thực của tham số m để phương trình 3x=m có nghiệm thực
 Xem đáp án
Xem đáp án
Đáp án đúng: D
* Lời giải
* Phương pháp giải
Do hàm ax > 0 nên để phương trình có nghiệm thực ta chỉ cần m>0
* Lý thuyết nắm thêm
Nguyên hàm.
- Định nghĩa
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng của R).
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi .
- Định lí 1.
Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
- Định lí 2.
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó là họ tất cả các nguyên hàm của f(x) trên K.
Kí hiệu:
- Chú ý: Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì dF(x) = F’(x)dx = f(x)dx.
Tính chất của nguyên hàm
- Tính chất 1.
Ví dụ 3.
- Tính chất 2.
(k là hằng số khác 0).
- Tính chất 3.
Bảng nguyên hàm của một số hàm số thường gặp

Phương pháp đổi biến số
- Định lí 1.
Nếu và u = u(x) là hàm số có đạo hàm liên tục thì:
Hệ quả: Nếu u = ax + b (a ≠ 0), ta có:
Phương pháp tính nguyên hàm từng phần.
- Định lí 2.
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
- Chú ý.
Vì u’(x) dx = du; v’(x) dx = dv. Nên đẳng thức trên còn được viết ở dạng:
Đó là công thức nguyên hàm từng phần.
Xem thêm các bài viết liên quan hay, chi tiết khác:
Câu 30:
19/01/2025Một tập hợp các ký hiệu và những quy tắc dùng để biểu diễn và tính toán giá trị các số được gọi là?
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải:
Một tập hợp các ký hiệu và những quy tắc dùng để biểu diễn và tính toán giá trị các số được gọi là hệ đếm
*Phương pháp giải
Một tập hợp các ký hiệu và những quy tắc dùng để biểu diễn và tính toán giá trị các số được gọi là hệ đếm
*Lý thuyết nắm thêm
| Biểu tượng | Tên ký hiệu | Ý nghĩa | Ví dụ |
| = | dấu bằng | bằng nhau | 5 = 2 + 35 bằng 2 + 3 |
| ≠ | dấu không bằng | không bằng nhau, khác | 5 ≠ 45 không bằng 4 |
| ≈ | dấu gần bằng | xấp xỉ | sin (0,01) ≈ 0,01,x ≈ y nghĩa là x xấp xỉ bằng y |
| > | dấu lớn hơn | lớn hơn | 5 > 45 lớn hơn 4 |
| < | dấu bé hơn | ít hơn | 4 < 54 nhỏ hơn 5 |
| ≥ | dấu lớn hơn hoặc bằng | lớn hơn hoặc bằng | 5 ≥ 4,x ≥ y có nghĩa là x lớn hơn hoặc bằng y |
| ≤ | dấu bé hơn hoặc bằng | ít hơn hoặc bằng | 4 ≤ 5,x ≤ y nghĩa là x nhỏ hơn hoặc bằng y |
| () | dấu ngoặc đơn | tính biểu thức bên trong đầu tiên | 2 × (3 + 5) = 16 |
| [] | dấu ngoặc vuông | tính biểu thức bên trong đầu tiên | [(1 + 2) × (1 + 5)] = 18 |
| + | dấu cộng | thêm vào | 1 + 1 = 2 |
| – | dấu trừ | phép trừ | 2 – 1 = 1 |
| ± | cộng – trừ | cả phép toán cộng và trừ | 3 ± 5 = 8 hoặc -2 |
| ± | trừ – cộng | cả phép toán trừ và cộng | 3 ∓ 5 = -2 hoặc 8 |
| * | dấu hoa thị | phép nhân | 2 * 3 = 6 |
| × | dấu nhân | phép nhân | 2 × 3 = 6 |
| ⋅ | dấu chấm nhân | phép nhân | 2 ⋅ 3 = 6 |
| ÷ | dấu phân chia | Phép chia | 6 ÷ 2 = 3 |
| / | dấu gạch chéo | phép chia | 6/2 = 3 |
| – | dấu gạch ngang | chia/phân số | 62 = 3 |
| mod | modulo | tìm số dư của phép chia | 7 mod 2 = 1 |
| . | dấu chấm thập phân | phân cách thập phân | 2.56 = 2 + 56/100 |
| a b | dấu lũy thừa | số mũ | 23 = 8 |
| a ^ b | dấu mũ | số mũ | 2^3 = 8 |
| √ a | dấu căn bậc hai | √ a ⋅ √ a = a | √ 9 = ± 3 |
| 3 √ a | dấu căn bậc ba | 3 √ a ⋅ 3 √ a ⋅ 3 √ a = a | 3 √ 8 = 2 |
| 4 √ a | dấu căn bậc bốn | 4 √ a ⋅ 4 √ a ⋅ 4 √ a ⋅ 4 √ a = a | 4 √ 16 = ± 2 |
| n √ a | dấu căn bậc n | với n = 3, n √ 8 = 2 | |
| % | dấu phần trăm | 1% = 1/100 | 10% × 30 = 3 |
| ‰ | dấu phần nghìn | 1 ‰ = 1/1000 = 0,1% | 10 ‰ × 30 = 0,3 |
| ppm | dấu một phần triệu | 1ppm = 1/1000000 | 10ppm × 30 = 0,0003 |
| ppb | dấu một phần tỷ | 1ppb = 1/1000000000 | 10ppb × 30 = 3 × 10 -7 |
| ppt | dấu một phần nghìn tỷ | 1ppt = 10 -12 | 10ppt × 30 = 3 × 10 -10 |
Xem thêm một số bài viết liên quan hay, chi tiết:
Câu 31:
19/01/2025Trên đường tròn lượng giác gốc A, cung lượng giác nào có các điểm biểu diễn tạo thành tam giác đều?
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải
Đáp án A: Cung lượng giác có số đo
Với ta có điểm M
Với ta có điểm N
Với ta có điểm A
Với ta có điểm M
Tương tự với các giá trị khác của k ta cũng chỉ thu được 3 điểm M, N, A trên đường tròn lượng giác và ba điểm đó tạo thành một tam giác đều nên A thỏa mãn
Đáp án B: Chỉ có hai điểm biểu diễn là A và A′ nên loại B.
Đáp án C: Có 4 điểm biểu diễn A, A′, B, B′ tạo thành hình vuông nên loại C.
Đáp án D: Có 6 điểm biểu diễn tạo thành hình lục giác đều nên loại D
*Phương pháp giải:
- Nắm vững lại tính chất về số đo cung tròn
* Các dạng bài tập và lý thuyết thêm về độ dài cung tròn:
a) Cho đường tròn (O; R) như hình sau:
- Một cung của đường tròn bán kính R và có số đo α rad có độ dài l = Rα,
trong đó: + R là bán kính đường tròn;
+ α là số đo bằng rad của cung tròn;
+ l là độ dài cung tròn.
- Một cung của đường tròn bán kính R và có số đo a° có độ dài l = ,
trong đó: + R là bán kính đường tròn;
+ a là số đo bằng độ của cung tròn;
+ l là độ dài cung tròn.
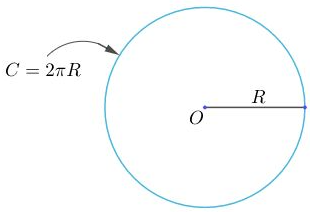
b) Công thức tính độ dài đường tròn (chu vi đường tròn)
Độ dài (C) của một đườn tròn bán kính R được tính theo công thức:
hoặc (với d = 2R)
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 32:
19/01/2025Để tính giờ địa phương, cần căn cứ vào
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
* Lời giải:
Trái Đất có dạng hình khối cầu và tự quay quanh trục từ tây sang đông, nên ở cùng một thời điểm, người đứng ở các kinh tuyến khác nhau sẽ nhìn thấy Mặt Trời ở các độ cao khác nhau, vì vậy các địa điểm thuộc các kinh tuyến khác nhau sẽ có giờ khác nhau, đó là giờ địa phương (hay giờ Mặt Trời).
* Phương pháp giải:
HỆ QUẢ CHUYỂN ĐỘNG TỰ QUAY QUANH TRỤC CỦA TRÁI ĐẤT
Giờ trên Trái Đất
- Trái Đất có dạng hình cầu và tự quay quanh trục từ tây sang đông, nên cùng một thời điểm, ở các kinh tuyến khác nhau sẽ nhìn thấy Mặt Trời ở độ cao khác nhau..
* Lý thuyết nắm thêm
NGUỒN GỐC HÌNH THÀNH TRÁI ĐẤT
- Nguồn gốc hình thành hệ Mặt Trời: thiên thể trong hệ Mặt Trời hình thành từ một đám mây bụi và khí lạnh hình đĩa với các vành xoắn ốc quay tương đối chậm. Ở trung tâm có khối lượng bụi lớn, nhiệt độ tăng lên rất cao có các phản ứng hạt nhân bắt đầu xuất hiện, đã hình thành Mặt Trời.

Hệ Mặt Trời
- Nguồn gốc hình thành Trái Đất: những vành xoắn ốc ở phía ngoài kết tụ lại dưới tác dụng của trọng lực và trở thành các hành tinh, trong đó có Trái Đất. Sự tăng nhiệt làm nóng chảy vật chất ở bên trong lòng trái đất và sắp xếp thành các lớp: nhân, bao man-ti và vỏ Trái Đất.
Đặc điểm vỏ Trái Đất
- Trái Đất có cấu trúc gồm ba lớp: vỏ, man-ti và nhân.
- Vỏ Trái Đất là phần cứng ngoài cùng, độ dày từ 5 km dưới đáy đại dương đến 70 km ở lục địa. Trên cùng của vỏ Trái Đất thường là tầng trầm tích, ở giữa là tầng đá granit làm thành nền của các lục địa. Dưới tầng granit là tầng badan thường lộ ra dưới đáy đại dương
- Vỏ Trái Đất được phân ra thành hai kiểu chính là vỏ lục địa và vỏ đại đương.
HỆ QUẢ CHUYỂN ĐỘNG TỰ QUAY QUANH TRỤC CỦA TRÁI ĐẤT
1. Sự luân phiên ngày, đêm
- Trái Đất có dạng hình cầu nên trong cùng một thời điểm chỉ được Mặt Trời chiếu sáng một nửa. Nửa được chiếu sáng là ngày, nửa không được chiếu sáng là đêm.
- Trái Đất không đứng yên mà tự quay quanh trục tưởng tượng của nó nên đã tạo ra sự luân phiên ngày và đêm trên Trái Đất.
2. Giờ trên Trái Đất
- Trái Đất có dạng hình cầu và tự quay quanh trục từ tây sang đông, nên cùng một thời điểm, ở các kinh tuyến khác nhau sẽ nhìn thấy Mặt Trời ở độ cao khác nhau..
- Trái Đất được chia làm 24 múi giờ (khu vực giờ), mỗi múi giờ rộng 15 độ kinh tuyến.
- Giờ ở múi số 0 được lấy làm giờ quốc tế hay giờ GMT (Greenwich Mean Time). Số thứ tự các múi giờ được đánh từ kinh tuyến gốc sang phía đông.
- Việt Nam thuộc múi giờ số 7.
- Trong thực tế, ranh giới các múi giờ không hoàn toàn chạy dọc theo kinh tuyến mà thường được quy định theo đường biên giới quốc gia.
- Quy định lấy kinh tuyến 180o qua giữa múi giờ số 12 ở Thái Bình Dương làm đường chuyển ngày quốc tế. Nếu đi từ tây sang đông, qua kinh tuyến 180o thì lùi 1 ngày lịch; đi từ đông sang tây, qua kinh tuyến 180o thì tăng 1 ngày lịch.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Địa lí 10 Bài 4 (Chân trời sáng tạo): Trái đất, thuyết kiến tạo mảng
TOP 15 câu Trắc nghiệm Địa Lí 10 Ôn tập chương 2 (Chân trời sáng tạo 2024) có đáp án: Trái Đất
Câu 33:
19/01/2025Đặt tính rồi tính tổng, biết các số hạng là:
a) 43 và 25; b) 20 và 68; c) 5 và 21
 Xem đáp án
Xem đáp án
* Lời giải:
a)
b)
c)
* Phương pháp giải:
- Đặt tính : Viết phép tính theo hàng dọc sao cho các chữ số cùng hàng thẳng cột với nhau.
- Tính : Cộng lần lượt các số theo thứ tự từ phải sang trái.
* Lý thuyết nắm thêm
Dạng 1: Thực hiện phép tính.
Để thực hiện phép tính bằng cách hợp lí nhất (tính nhanh), ta cần đưa về tổng, hiệu, tích, thương của số tròn chục, tròn trăm, tròn nghìn … và áp dụng các tính chất:
+ Tính chất kết hợp của phép cộng.
+ Tính chất kết hợp của phép nhân.
+ Chia một tổng cho một số.
Dạng 2: Tìm x.
Xác định vai trò của số đã biết và số chưa biết trong phép tính, sau đó áp dụng:
+ Phép cộng: Số hạng chưa biết = Tổng – Số hạng đã biết.
+ Phép trừ: Số trừ = Số bị trừ – Hiệu; Số bị trừ = Hiệu + Số trừ.
+ Phép nhân: Thừa số chưa biết = Tích : Thừa số đã biết.
+ Phép chia hết: Số chia = Số bị chia : Thương; Số bị chia = Số chia . Thương.
Dạng 3: Bài toán có lời văn.
Dạng 4: Toán về phép chia có dư.
Trong phép chia có dư:
+ Số bị chia = Số chia x Thương + Số dư (0 < Số dư < Số chia).
+ Số chia = (Số bị chia – Số dư) : Thương.
+ Thương = (Số bị chia – Số dư) : Số chia.
+ Số dư = Số bị chia – Số chia x Thương.
Dạng 5: Tìm số chưa biết trong một phép tính.
+ Phép cộng và phép trừ: Tính lần lượt theo cột từ phải sang trái. Chú ý những trường hợp có “nhớ”.
+ Phép nhân: Thực hiện phép nhân từ phải sang trái, suy luận từng bước để tìm ra những số chưa biết.
+ Phép chia: Đặt tính và lần lượt thực hiện phép chia từ hàng lớn nhất.
Xem thêm các bài viết liên quan hay, chi tiết:
Toán lớp 5 trang 9 (Kết nối tri thức) Ôn tập các phép tính với số tự nhiên
Bài thi liên quan
-
Tổng hợp câu hỏi môn Toán (phần 1)
-
200 câu hỏi
-
0 phút
-
-
Tổng hợp câu hỏi môn Toán (phần 3)
-
78 câu hỏi
-
0 phút
-