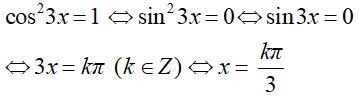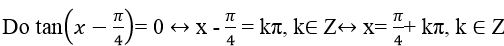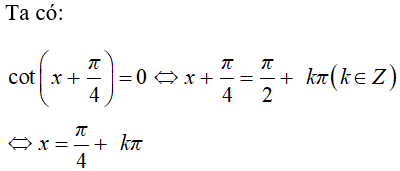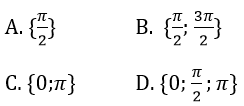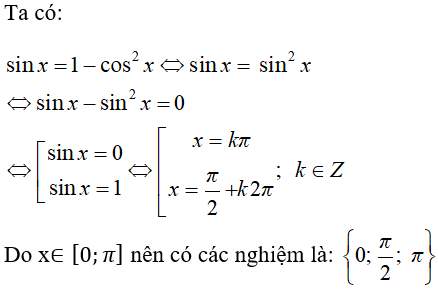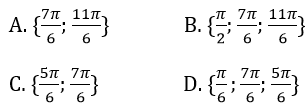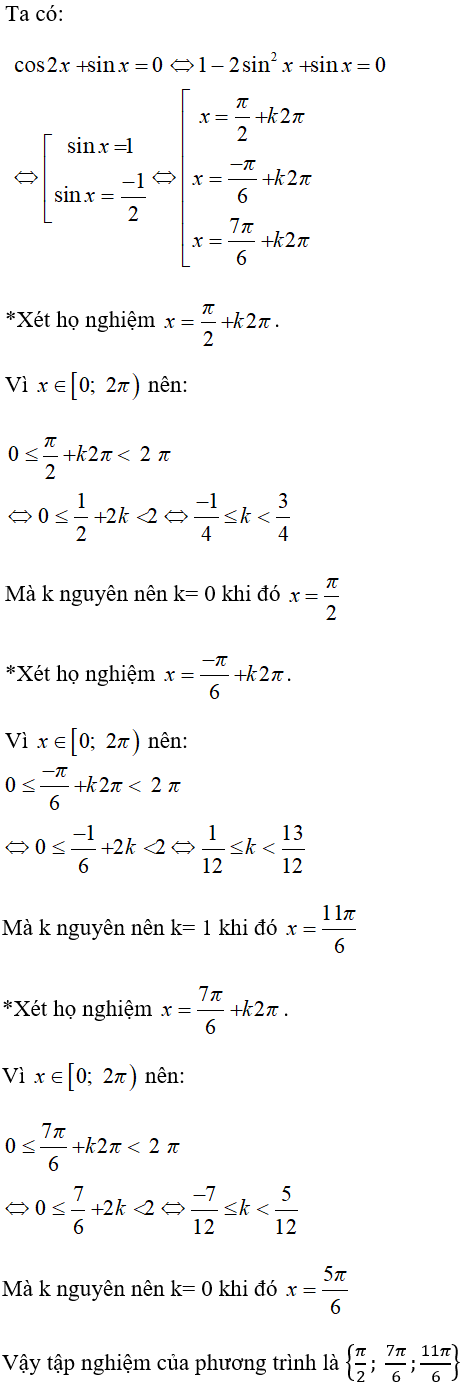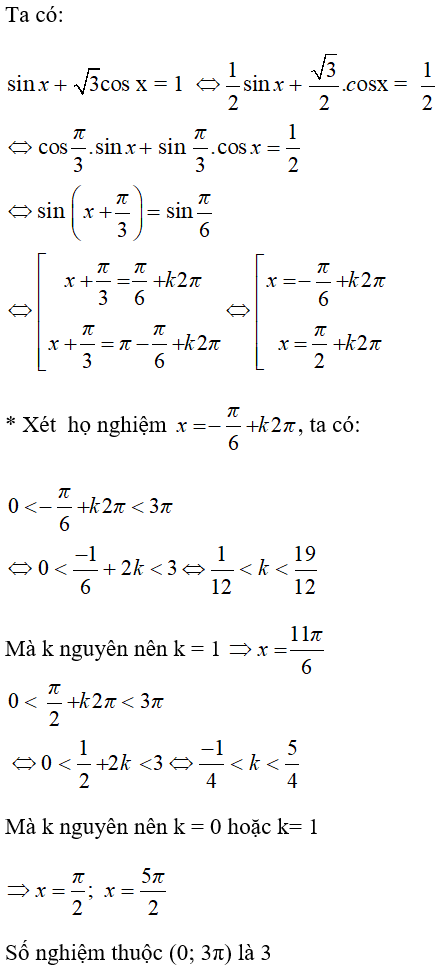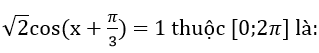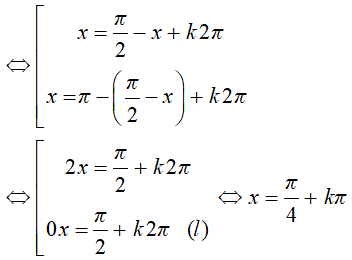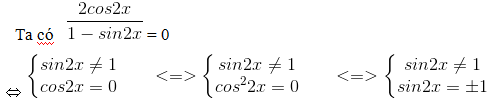Nội dung bài viết

    Xem thêm

    50 Bài tập Phương trình lượng giác cơ bản Toán 11 mới nhất

    Với 50 Bài tập Phương trình lượng giác cơ bản Toán lớp 11 mới nhất được biên soạn bám sát chương trình Toán 11 giúp các bạn học tốt môn Toán hơn.

    Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:

    1 32,122 25/08/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Bài tập Phương trình lượng giác cơ bản - Toán 8

    I. Bài tập trắc nghiệm

    Bài 1: Phương trình cos23x = 1 có nghiệm là:

    A. x = kπ, k ∈ Z.     

    B. x =kπ2, k ∈ Z.

    C. x =kπ3, k ∈ Z.     

    D. x =kπ4, k ∈ Z.

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án C

    Bài 2: Phương trình tan( x - π4) = 0 có nghiệm là:

    A. x = π4 + kπ, k ∈ Z.     

    B. x = 3π4 + kπ, k ∈ Z.

    C. x = kπ, k ∈ Z.     

    D. x = k2π, k ∈ Z.

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án A

    Bài 3: Phương trình cot( x + π4) = 0 có nghiệm là:

    A. x = - π4 + kπ, k ∈ Z.     

    B. x = π4 + kπ, k ∈ Z.

    C. x = - π4 + k2π, k ∈ Z.     

    D. x = π4 + k2π, k ∈ Z.

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án B

    Bài 4: Trong [0;π],phương trình sinx = 1 – cos2x có tập nghiệm là:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án D

    Bài 5: Trong [0;2 π), phương trình cos2x + sinx = 0 có tập nghiệm là:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án B

    Bài 6: Trong [0;2 π), phương trình sin2x + sinx = 0 có số nghiệm là:

    A. 1      

    B. 2

    C. 3      

    D. 4

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án D

    Bài 7: Phương trình sinx + 3cosx = 1 có số nghiệm thuộc (0;3π) là:

    A. 2      

    B. 3

    C. 4      

    D. 6

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án B

    Bài 8: Phương trình 2cos(x + π3) = 1 có mấy họ nghiệm?

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

    A. 0      

    B. 2

    C. 1      

    D. 3

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án B

    Bài 9: Số nghiệm của phương trình sin(x +π4) = 1 thuộc [0;3π] là:

    A. 1      

    B. 0

    C. 2      

    D. 3

    Lời giải:

    Bài 10: Phương trình sinx = cosx có số nghiệm thuộc đoạn [0;π] là:

    A. 1

    B. 4

    C. 5

    D. 2

    Lời giải:

    Ta có sinx = cosx ⇒ sinx = sin(π2 – x)

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Do x ∈ [0;π] nên k = 0. Vậy chỉ có 1 nghiệm của phương trình thuộc [0;π].

    Chọn đáp án A

    II. Bài tập tự luận có giải

    Bài 1: Phương trình sin2x = 1 có nghiệm là?

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 2: Phương trình sin2 x3 = 1 có nghiệm là?

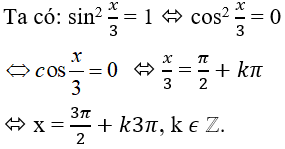
    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án C

    Bài 3 Phương trình 2cosx - 3 = 0 có tập nghiệm trong khoảng (0;2π) là?

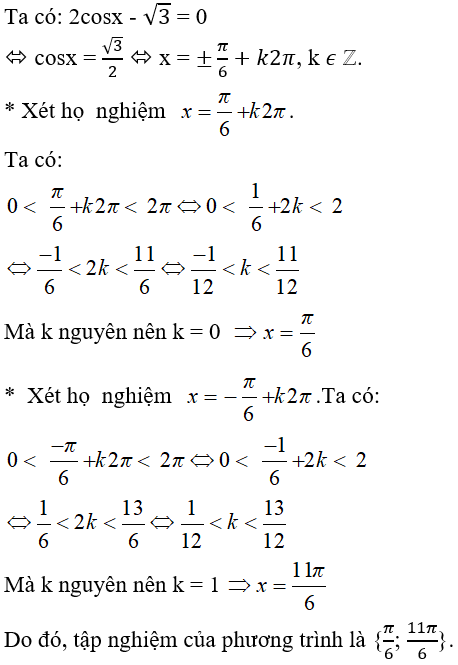
    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 4 Phương trình sin(πcos2x) = 1 có nghiệm là?

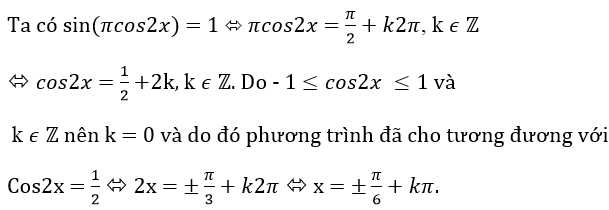
    Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 5 Phương trình cosx2 = - 1 có nghiệm là?

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 6: Giải các phương trình sau:

    a)\sin(x+2)=\frac{1}{3}

    b)\sin3x=1

    c)\sin(\frac{2x}{3}-\frac{\pi}{3})=0

    d)\sin(2x+ 20^{\circ} )=\frac{(-\sqrt{3})}{2}

    Lời giải:

    a)\sin(x+2)=\frac{1}{3}

    Giải bài tập trang 28, 29 SGK Giải tích 11

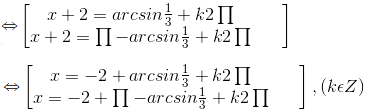
    b) sin3x = 1 ⇔ 3x = π2 + k2π

    ⇔ x = π6 + k(2π3), (k ∈ Z).

    c)\sin(\frac{2x}{3}-\frac{\pi}{3})=0

    \Leftrightarrow \frac{2x}{3}-\frac{\pi}{3}=k\pi\ \Rightarrow \ x\ =\ \frac{\pi}{2}\ +\frac{3\pi}{2}k

    (k ∈ Z).

    d) Vì -32 = sin(-600) nên phương trình đã cho tương đương với sin (2x + 200) = sin(-600)

    ⇔Giải bài tập trang 28, 29 SGK Giải tích 11

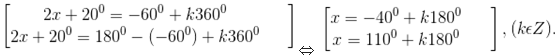
    Bài 7 Với những giá trị nào của x thì giá trị của các hàm số y = sin3x và y = sinx bằng nhau?

    x thỏa mãn yêu cầu bài ra khi và chỉ khi

    Giải bài tập trang 28, 29 SGK Giải tích 11

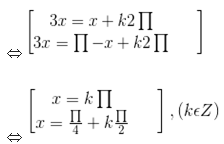
    Bài 8 Giải các phương trình sau:

    a) cos(x – 1) = 23

    b) cos3x = cos120

    c) cos(3x2 – π4) = -12

    d) cos22x = 14

    Lời giải:

    a) cos(x - 1) = 23 ⇔ x - 1 = ±arccos23 + k2π

    ⇔ x = 1 ± arccos23 + k2π, (k ∈Z)

    b) cos3x = cos120 ⇔ 3x = ±120 + k3600 ⇔ x = ±40 + k1200, (k ∈ Z).

    c) Vì -12 = cos2π3 nên cos(3x2 - π4) = -12 ⇔ cos(3x2 - π4) = cos23 ⇔ 3x2 - π4 = ±2π3 + k2π ⇔ x = 23(π4 + 2π3) + 4kπ3

    Giải bài tập trang 28, 29 SGK Giải tích 11

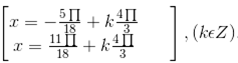
    d) Sử dụng công thức hạ bậc 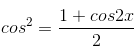Giải bài tập trang 28, 29 SGK Giải tích 11 (suy ra trực tiếp từ công thức nhan đôi) ta có

    cos22x = 14 ⇔ 1 + cos4x2 = 14 ⇔ cos4x = -12

    ⇔ 4x = ±2π3 + 2kπ ⇔ x = ±π6 + kπ2, (k ∈ Z)

    Bài 9 Giải phương trình 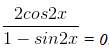Giải bài tập trang 28, 29 SGK Giải tích 11

    Giải bài tập trang 28, 29 SGK Giải tích 11

    ⇔ sin2x = -1 ⇔ 2x = -π2 + k2π ⇔ x = -π4 + kπ, (k ∈ Z).

    Bài 10 Giải các phương trình sau:

    a) tan(x – 150) = 33 b) cot(3x – 1) = -3

    c) cos2x . tanx = 0 d) sin3x . cotx = 0

    Lời giải:

    a) Vì 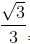Giải bài tập trang 28, 29 SGK Giải tích 11= tan300 nên tan(x – 150) = 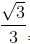Giải bài tập trang 28, 29 SGK Giải tích 11 ⇔ tan(x – 150) = tan300 ⇔ x – 150 = 300 + k1800 ⇔ x = 450 + k1800, (k ∈ Z).

    b) Vì -3 = cot(-π6) nên cot(3x – 1) = -3 ⇔ cot(3x – 1) = cot(-π6)

    ⇔ 3x – 1 = -π6 + kπ ⇔ x = -π18 + 13 + k(π3), (k ∈ Z)

    c) Đặt t = tan x thì cos2x = 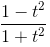Giải bài tập trang 28, 29 SGK Giải tích 11 , phương trình đã cho trở thành
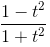    Giải bài tập trang 28, 29 SGK Giải tích 11. t = 0 ⇔ t ∈ {0; 1; -1} .

    Vì vậy phương trình đã cho tương đương với

    Giải bài tập trang 28, 29 SGK Giải tích 11

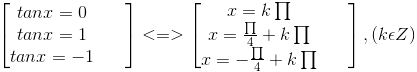
    d) sin3x . cotx = 0

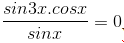    ⇔ Giải bài tập trang 28, 29 SGK Giải tích 11Với điều kiện sinx # 0, phương trình tương đương với

    sin3x . cosx = 0 ⇔ sin3x = 0; cos3x = 0

    Với cosx = 0 ⇔ x = π2 + kπ, k ∈ Z thì sin2x = 1 – cos2x = 1 – 0 = 1 => sinx # 0, điều kiện được thỏa mãn.

    Với sin3x = 0 ⇔ 3x = kπ ⇔ x = k(π3), (k ∈ Z). Ta còn phải tìm các k nguyên để x = k(π3) vi phạm điều kiện (để loại bỏ), tức là phải tìm k nguyên sao cho sink(π3) = 0, giải phương trình này (với ẩn k nguyên), ta có sink(π3) = 0 ⇔ k(π3)= lπ, (l ∈ Z) ⇔ k = 3l ⇔ k : 3.

    Do đó phương trình đã cho có nghiệm là x = π2 + kπ, (k ∈Z) và x = k(π3) (với k nguyên không chia hết cho 3).

    Nhận xét: Các em hãy suy nghĩ và giải thích tại sao trong các phần a, b, c không phải đặt điều kiện có nghĩa và cũng không phải tìm nghiệm ngoại lai.

    III. Bài tập vận dụng 

    Bài 1 Giải các phương trình sau

    a) sin⁡(x+2)=13.

    b) sin⁡3x=1.

    c) sin⁡(2x3−π3)=0

    d) sin⁡(2x+200)=−32.

    Bài 2 Với những giá trị nào của x thì giá trị của các hàm số y = sin3x và y = sin x bằng nhau?

    Bài 3 Giải các phương trình sau:

    a) cos⁡(x−1)=23.

    b) cos⁡3x=cos⁡120.

    c). cos⁡(3x2−π4)=−12.

    d) cos2⁡2x=14.

    Bài 4 Giải phương trình 2cos2x1-sin2x=0

    Bài 5 Giải các phương trình sau

    a) tan⁡(x−150)=33.

    b) cot⁡(3x−1)=−3.

    Bài 6 Giải các phương trình sau

    a) cos⁡2x.tanx=0.

    b) sin⁡3x.cot⁡x=0.

    Bài 7 Giải các phương trình sau

    a) tan⁡(x−150)=33.

    b) cot⁡(3x−1)=−3

    Bài 8 Giải các phương trình sau

    a) cos⁡2x.tanx=0.

    b) sin⁡3x.cot⁡x=0.

    Bài 9 Giải các phương trình sau

    a) sin⁡3x−cos⁡5x=0.

    b) tan⁡3x.tan⁡x=1.

    Bài 10 Giải các phương trình sau:

    a) sin3x – cos5x = 0 b) tan3x . tanx = 1.

    Xem thêm các bài Bài tập Toán lớp 11 hay, chi tiết khác:

    Bài tập Hàm số lượng giác

    Bài tập Một số phương trình lượng giác thường gặp

    Bài tập Một số phương trình lượng giác cơ bản

    Bài tập Quy tắc đếm

    Bài tập Hoán vị - Chỉnh hợp - Tổ hợp

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 32,122 25/08/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: