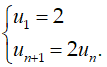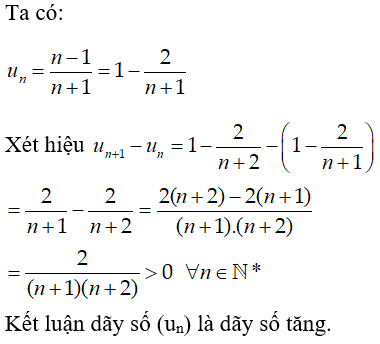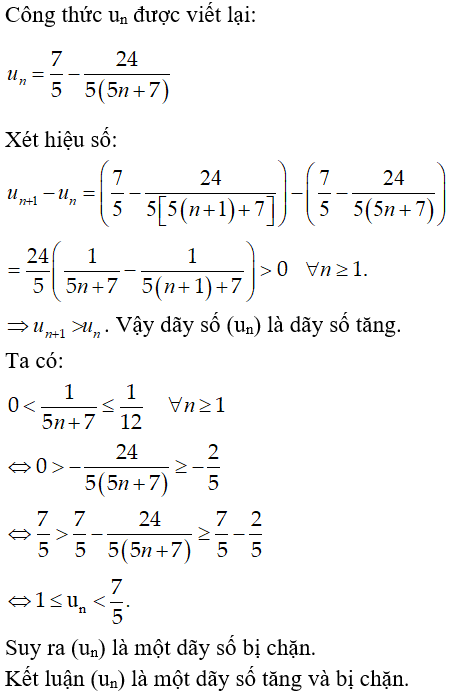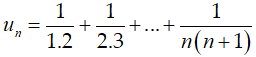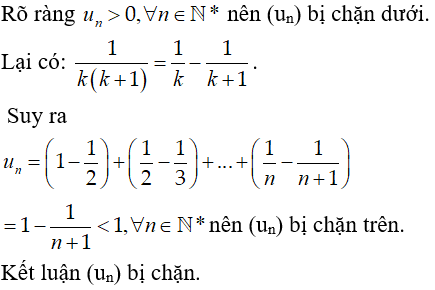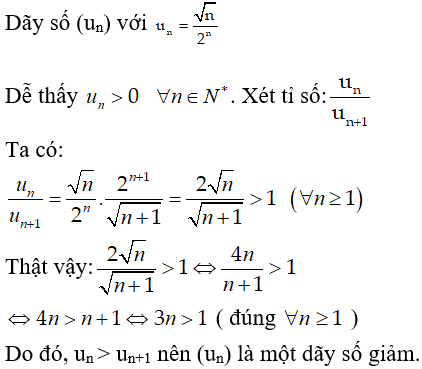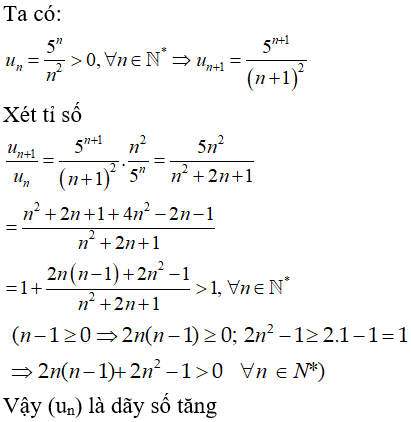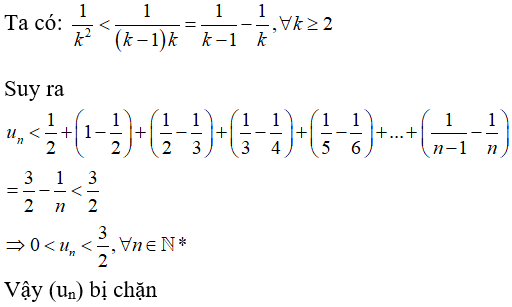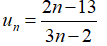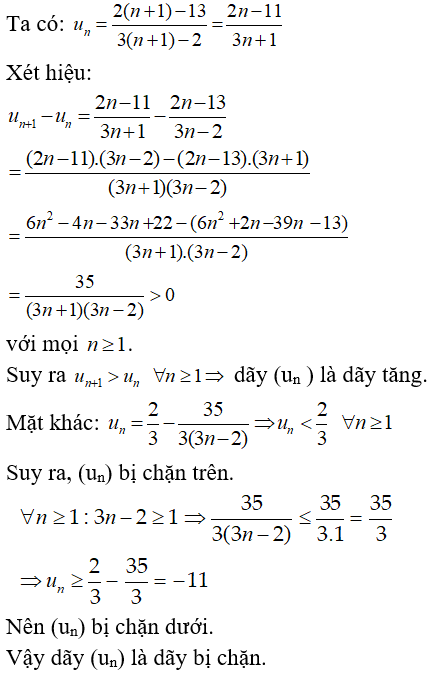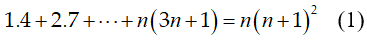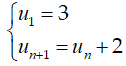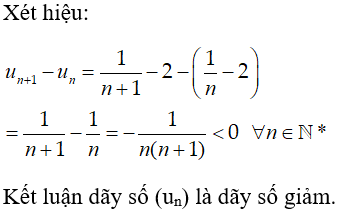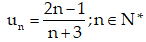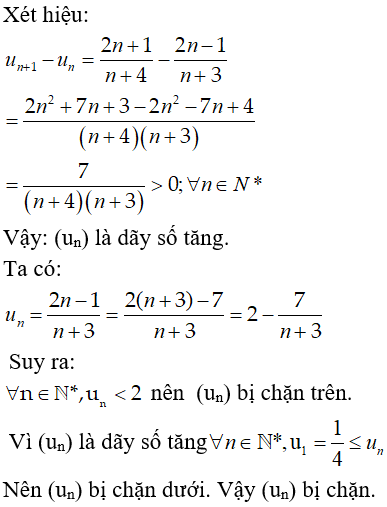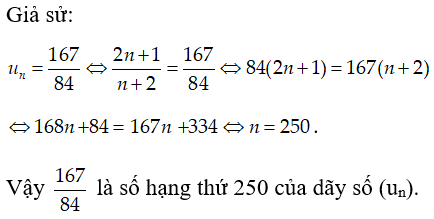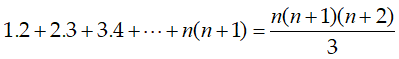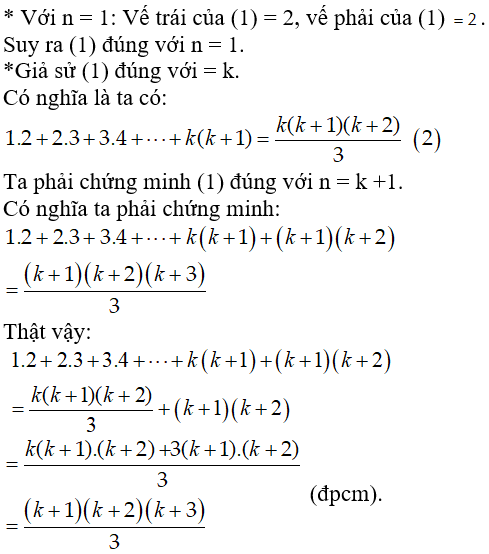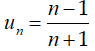Nội dung bài viết

    Xem thêm

    50 Bài tập Phương pháp quy nạp toán học - Dãy số Toán 11 mới nhất

    Với 50 Bài tập Phương pháp quy nạp toán học - Dãy số Toán lớp 11 mới nhất được biên soạn bám sát chương trình Toán 11 giúp các bạn học tốt môn Toán hơn.

    Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:

    1 1,151 29/08/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Bài tập Phương pháp quy nạp toán học - Dãy số - Toán 11

    I. Bài tập trắc nghiệm

    Bài 1: Chứng minh bằng phương pháp quy nạp n3 + 11n chia hết cho 6.

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 2: Tìm công thức tính số hạng tổng quát un theo n của dãy số sau Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    A. un = n2 - 3n + 10

    B. un = 2n

    C. un = 2n

    D. un = n + 2

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Vậy (*) đúng với n = k + 1. Kết luận (*) đúng với mọi số nguyên dương n.

    Chọn đáp án B

    Bài 3: Xét tính tăng giảm của dãy số (un) biết: Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    A. Dãy số giảm.

    B. Dãy số không tăng không giảm

    C. Dãy số không đổi.

    D. Dãy số tăng

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án D

    Bài 4: Cho dãy số Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11. Tìm mệnh đề đúng?

    A. Dãy số tăng và bị chặn.

    B. Dãy số giảm và bị chặn.

    C. Dãy số tăng và bị chặn dưới

    D. Dãy số giảm và bị chặn trên.

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án A

    Bài 5: Xét tính bị chặn của dãy số (un) biết: Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    A. Dãy số bị chặn trên

    B. Dãy số bị chặn dưới.

    C. Dãy số bị chặn

    D. Tất cả sai.

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án C

    Bài 6: Cho dãy số (un) xác định bởi 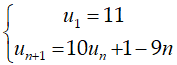Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11. Tìm số hạng tổng quát un theo n.

    A. un = 100 + 2n

    B.un = 10n + n

    C. un = 100n – n2

    D. Đáp án khác

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án B

    Bài 7: Xét tính tăng giảm của dãy số (un) với Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    A. Dãy số tăng

    B. Dãy số giảm

    C. Dãy số không tăng, không giảm

    D. Dãy số không đổi.

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án A

    Bài 8: Cho dãy số (un) biết Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 . Mệnh đề nào sau đây đúng?

    A. Dãy số tăng

    B. Dãy số giảm

    C. Dãy số không tăng, không giảm

    D. Dãy số là dãy hữu hạn

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án A

    Bài 9: Cho dãy số (un) biết Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 . Mệnh đề nào sau đây đúng ?

    A. Dãy số bị chặn dưới.

    B. Dãy số bị chặn trên.

    C. Dãy số bị chặn.

    D. Không bị chặn

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án C

    Bài 10: Xét tính tăng, giảm và bị chặn của dãy số (un), biết: Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    A. Dãy số tăng, bị chặn

    B. Dãy số giảm, bị chặn

    C. Dãy số không tăng không giảm, không bị chặn

    D. Cả A, B, C đều sai

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án A

    II. Bài tập tự luận có lời giải

    Bài 1: Chứng minh rằng với mọi số nguyên n, ta có:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Vậy (1) đúng với n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

    Bài 2: Với mỗi số nguyên dương n, gọi un = 9n - 1. Chứng minh rằng với mọi số nguyên dương n thì un luôn chia hết cho 8.

    Lời giải:

    * Ta có u1 = 9.1 - 1 = 8 chia hết cho 8 (đúng với n = 1).

    * Giả sử uk = 9k - 1 chia hết cho 8.

    Ta cần chứng minh uk + 1 = 9k + 1 - 1 chia hết cho 8.

    Thật vậy, ta có:

    uk + 1 = 9k + 1 - 1 = 9.9k - 1 = 9(9k - 1) + 8 = 9uk + 8.

    Vì 9uk và 8 đều chia hết cho 8, nên uk + 1 cũng chia hết cho 8.

    Vậy với mọi số nguyên dương n thì un chia hết cho 8.

    Bài 3: Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có: 2n + 1 > 2n + 3 (*)

    Lời giải:

    * Với n = 2 ta có 2.2+1 > 2.2 + 3 ⇔ 8 > 7 (đúng).

    Vậy (*) đúng với n = 2 .

    * Giả sử với n = k, k ≥ 2 thì (*) đúng, có nghĩa ta có: 2k + 1 > 2k + 3 (1).

    * Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh:

    2k + 2 > 2(k + 1) + 3

    Thật vậy, nhân hai vế của (1) với 2 ta được:

    2.2k + 1 > 2(2k + 3) ⇔ 2k + 2 > 4k + 6 > 2k + 5.

    (vì 4k + 6 > 4k + 5 > 2k + 5)

    Hay 2k + 2 > 2(k + 1)+ 3

    Vậy (*) đúng với n = k + 1.

    Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương n ≥ 3 .

    Bài 4: Tìm công thức tính số hạng tổng quát un theo n của dãy số sau Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 5: Xét tính tăng giảm của dãy số (un) biết: Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án B

    Bài 6: Xét tính tăng hay giảm và bị chặn của dãy số : Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Chọn đáp án C

    Bài 7: Cho dãy số (un) có số hạng tổng quát Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11. Số 16784 là số hạng thứ mấy?

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 8: Chứng minh bằng quy nạp:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Lời giải:

    Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Vậy (1) đúng khi n= k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

    Bài 9:

    Chứng minh rằng với n ∈ N*, ta có các đẳng thức:

    a. 2+5+8+...+3n-1=\frac{n\left( 3n+1 \right)}{2}   (1)

    b. \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{{{2}^{6}}}=\frac{{{2}^{n-2}}}{{{2}^{n}}}              (2)

    c. {{1}^{2}}+{{2}^{2}}+{{3}^{2}}+...+{{n}^{2}}=\frac{n\left( n+1 \right)\left( 2n+1 \right)}{6}       (3)

    Lời giải:

    a. Với n = 1, ta có:

    VT = 3 – 1 = 2

    VP = \dfrac{3 + 1}{2}

    Vậy VT = VP (1) đúng với n = 1

    Giả thiết (1) đúng với n = k ≥ 1 nghĩa là:

    2 + 5 + 8 + …+3k – 1 = \dfrac{k(3k+1)}{2} (1a)

    Ta chứng minh (1a) đúng với n = k + 1 nghĩa là chứng minh:

    2+5+8+...+3k-1+3(k+1)-1=\dfrac{(k+1)[3(k+1)+1]}{2}

    \begin{align} & \left( 1a \right)\Leftrightarrow 2+5+8+...+3k-1+3\left( k+1 \right)-1 \\ & =\frac{k\left( 3k+1 \right)}{2}+3\left( k+1 \right)-1 \\ & =\frac{3{{k}^{2}}+7k+4}{2}=\frac{\left( k+1 \right)\left( 3k+4 \right)}{2} \\ \end{align}

    \Rightarrow(1) đúng với n = k +1, vậy (1a) đúng với n\in \mathbb{N}

    b. \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{{{2}^{n}}}=\frac{{{2}^{n}}-1}{{{2}^{n}}}

    Với n = 1 thì \left\{ \begin{matrix} VT=\dfrac{1}{2} \\ VP=\dfrac{1}{2} \\ \end{matrix}\Rightarrow VT=VP \right.

    Vậy (2) đúng với n = 1

    Giả sử đẳng thức đúng với n = k, tức là:

    \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{{{2}^{k}}}=\frac{{{2}^{k}}-1}{{{2}^{k}}}

    Khi đó ta chứng minh (2) đúng với n = k +1

    Ta có :

    \begin{align} & \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{{{2}^{k}}}+\frac{1}{{{2}^{k+1}}}=\frac{{{2}^{k}}-1}{{{2}^{k}}}+\frac{1}{{{2}^{k+1}}} \\ & =\frac{{{2}^{k+1}}-2}{{{2}^{k+1}}}+\frac{1}{{{2}^{k+1}}}=\frac{{{2}^{k+1}}-1}{{{2}^{k+1}}} \\ \end{align}

    (2) đúng với n = k + 1. Vậy nó đúng với mọi n ∈ N*

    c. {{1}^{2}}+{{2}^{2}}+{{3}^{2}}+...+{{n}^{2}}=\frac{n\left( n+1 \right)\left( 2n+1 \right)}{6} (3)

    Khi n = 1 vế trái bằng 1

    VP=\frac{1\left( 1+1 \right)\left( 2+1 \right)}{6}=1\Rightarrow VT=VP

    Vậy (3) đúng với n = 1

    Giả sử đẳng thức (3) đúng với n = k nghĩa là:

    {{1}^{2}}+{{2}^{2}}+{{3}^{2}}+...+{{k}^{2}}=\frac{k\left( k+1 \right)\left( 2k+1 \right)}{6} (3a)

    Ta phải chứng minh (3a) đúng khi n = k + 1

    + Ta cộng 2 vế của (3) cho (k + 1)2

    \begin{align} & {{1}^{2}}+{{2}^{2}}+{{3}^{2}}+...+{{k}^{2}}+{{\left( k+1 \right)}^{2}} \\ & =\frac{k\left( k+1 \right)\left( 2k+1 \right)}{6}+{{\left( k+1 \right)}^{2}} \\ & =\frac{\left( k+1 \right)}{6}\left[ k\left( 2k+1 \right)+6\left( k+1 \right) \right] \\ & =\frac{\left( k+1 \right)}{6}\left( 2{{k}^{2}}+7k+6 \right) \\ & =\frac{\left( k+1 \right)\left( k+2 \right)\left( 2k+3 \right)}{6} \\ & =\frac{\left( k+1 \right)\left[ \left( k+1 \right)+1 \right]\left[ 2\left( k+1 \right)+1 \right]}{6} \\ \end{align}

    Vậy đẳng thức đúng với n = k + 1. Do đó, đẳng thức đúng với mọi n ∈ N*

    Bài 10 Chứng minh rằng với n ∈ N*

    a. n3 + 3n2 + 5n chia hết cho 3.

    b. 4^n + 15n – 1 chia hết cho 9

    c. n3 + 11n chia hết cho 6.

    Lời giải:

    Đặt An = n^3 + 3n^2 + 5n

    + Ta có: với n = 1

    A_1 = 1 + 3 + 5 = 9 chia hết 3

    + Giả sử với n = k ≥ 1 ta có:

    A_k = (k^3 + 3k^2 + 5k) chia hết 3 (giả thiết quy nạp)

    + Ta chứng minh A_{k + 1} chia hết 3

    Thật vậy, ta có:

    A_{k + 1} = (k + 1)^3 + 3(k + 1)^2 + 5(k + 1)

    = k^3 + 3k^2 + 3k + 1 + 3k^2 + 6k + 3 + 5k + 5

    = (k^3 + 3k^2 + 5k) + 3k^2 + 9k + 9

    Theo giả thiết quy nạp A_k chia hết 3, hơn nữa 9(k + 1) chia hết 3

    Nên A_n = n3 + 3n2 + 5n chia hết cho 3 với mọi ∀n ∈ N*

    b. 4n + 15n – 1 chia hết cho 9

    Đặt A_n = 4^n + 15n – 1

    với n = 1 => A_1 = 4 + 15 – 1 = 18 chia hết 9

    + Giả sử với n = k ≥ 1 ta có:

    A_k = (4^k + 15k – 1) chia hết 9 (giả thiết quy nạp)

    + Ta chứng minh: A_{k+1} chia hết 9

    Thật vậy, ta có:

    Ak+1 = (4k+1 + 15(k + 1) – 1) = 4k.41 + 15k + 15 – 1

    = (4k + 15k – 1) + (3.4k + 15) = Ak + 3(4k + 5)

    Theo giả thiết quy nạp A_k chia hết 9, hơn nữa:

    3(4k + 5) chia hết 9 ( chứng minh tương tự) ∀k ≥ 1 nên A_{k+1} chia hết 9

    Vậy An = 4n + 15n – 1 chia hết cho 9 ∀n ∈ N*

    c. n3 + 11n chia hết cho 6.

    Đặt Un = n3 + 11n

    + Với n = 1 => U1 = 12 chia hết 6

    + Giả sử với n = k ≥ 1 ta có:

    U_k = (k^3 + 11k) chia hết 6 (giả thiết quy nạp)

    Ta chứng minh: Uk+1 chia hết 6

    Thật vậy ta có:

    Uk+1 = (k + 1)3 + 11(k +1) = k^3 + 3k^2 + 3k + 1 + 11k + 11

    = (k^3 + 11k) + 3k^2 + 3k + 12 = U_k + 3(k^2 + k + 4)

    + Theo giả thiết quy nạp thì:

    U_k chia hết 6, hơn nữa 3(k^2 + k + 4) = 3(k(k+1)+4) chia hết 6 ∀k ≥ 1 (2 số liên tiếp nhân với nhau chia hết cho 2)

    Do đó: Uk+1 chia hết 6

    Vậy: Un = n3 + 11n chia hết cho 6 ∀n ∈ N*

    III. Bài tập vận dụng

    Bài 1 Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có các bất đẳng thức:

    a. 3n > 3n + 1

    b. 2n+1 > 2n + 3

    Bài 2 Cho tổng {{S}_{n}}=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{n\left( n+1 \right)} với n\in {{\mathbb{N}}^{*}}

    a. Tính S1, S2, S3

    b. Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.

    Bài 3 Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là \dfrac{n(n-3)}{2}

    Bài 4 Chứng minh rằng với n Є N*, ta có đẳng thức:

    a) 2 + 5+ 8+.... + 3n - 1 = n(3n+1)2;

    b) 12+14+18+...+12n=2n−12n;

    c) 12 + 22 + 32 +….+ n2 = n(n+1)(2n+1)6.

    Bài 5 Chứng minh rằng với n ε  N*    ta luôn có:

    a) n3 + 3n2 + 5n chia hết cho 3;

    b) 4n + 15n - 1 chia hết cho 9;

    c) n3 + 11n chia hết cho 6.

    Bài 6 Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta có các bất đẳng thức:

    a) 3n > 3n + 1;                  

    b) 2n + 1 > 2n + 3

    Bài 7

    Giải Bài 1: Phương pháp quy nạp toán học

    a) Tính S1, S2, S3.

    b) Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.

    Bài 8 Tìm công thức tính số hạng tổng quát un theo n của dãy số sau Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 9 Xét tính tăng giảm của dãy số (un) biết: Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

    Bài 10 Cho dãy số 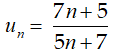Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11. Tìm mệnh đề đúng?

    Xem thêm các bài Bài tập Toán lớp 11 hay, chi tiết khác:

    Bài tập Cấp số cộng

    Bài tập Cấp số nhân

    Bài tập Giới hạn của dãy số

    Bài tập Giới hạn của hàm số

    Bài tập Hàm số liên tục

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,151 29/08/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: