25 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Cung và góc lượng giác cơ bản (P3)

Câu 1:

18/07/2024

Một đường tròn có bán kính R = 10. Độ dài cung 40⁰ trên đường tròn gần bằng:

A. 7

B. 9

C. 10

D. 8

Xem đáp án

Chọn A.

Độ dài của cung 40⁰ trên đường tròn được tính bằng công thức:

Câu 2:

20/07/2024

Một đường tròn có bán kính 20 cm. Hỏi độ dài của cung trên đường tròn đó có số đo π/15 gần với giá trị nào nhất.

A. 4,1

B. 4,2

C. 4,3

D. 4,4

Xem đáp án

Chọn B.

Độ dài của cung trên đường tròn được tính bằng công thức:

Câu 3:

18/07/2024

Chọn điểm A(1 ; 0) là điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm cuối M của cung lượng giác có số đo 25π/4.

A. M là điểm chính giữa của cung phần tư thứ I.

B. M là điểm chính giữa của cung phần tư thứ II.

C. M là điểm chính giữa của cung phần tư thứ III.

D. M là điểm chính giữa của cung phần tư thứ IV.

Xem đáp án

Chọn A.

Theo giả thiết ta có:

suy ra điểm M là điểm chính giữa của cung phần tư thứ I.

Câu 4:

22/07/2024

Cho góc α thỏa mãn $\cos a = \frac{3}{5} v à \frac{- π}{2} < a < 0$ .Tính $\sqrt{5 + 3 \tan α} + \sqrt{6 - 4 c o t α}$

A. 4

B. -2

C. -6

D. 3

Xem đáp án

Chọn A.

Ta có

Thay vào P ta được P = 4.

Câu 5:

23/07/2024

Biểu thức $A = \frac{\cos 750^{o} + \sin 420^{o}}{\sin (- 330^{o}) - \cos (- 390^{o})}$ có giá trị rút gọn bằng

A. $- 3 - \sqrt{3}$

B. $2 - 3 \sqrt{3}$

C. $\frac{2 \sqrt{3}}{\sqrt{3} - 1}$

D.Tất cả sai

Xem đáp án

Chọn A.

Ta có: 750⁰= 2.360⁰+ 30⁰; 420⁰= 360⁰+ 60⁰; -330⁰= -360⁰+ 30⁰; -390⁰= -360⁰- 30⁰

Nên từ giả thiết ta suy ra:

Câu 6:

10/11/2024

Đơn giản biểu thức $A = \cos (a - \frac{π}{2}) + \sin (a - π)$ ta được:

A. A = cos + sina

B. A = 2sina

C. A = 0

D. Tất cả sai

Xem đáp án

Đáp án đúng là C.

Lời giải

Do hai góc phụ nhau thì sin góc này bằng cos góc kia; hai góc bù nhau thì sin bằng nhau nên ta có:

Hay A= sin α - sinα = 0.

*Phương pháp giải:

Sử dụng công thức chu kì và hai góc phụ nhau, bù nhaun để tính giá trị của biểu thức.

*Lý thuyết:

Đối với hai góc bù nhau, α và 180° – α, ta có:

sin (180° – α) = sin α;

cos (180° – α) = - cos α;

tan (180° – α) = - tan α (α ≠ 90°);

cot (180° – α) = - cot α (0° < α < 180°).

Chú ý:

- Hai góc bù nhau có sin bằng nhau ; có côsin , tang, côtang đối nhau.

Xem thêm

Tổng hợp lý thuyết Chương 3 – Toán 10 Kết nối tri thức

TOP 30 câu Trắc nghiệm Ôn tập chương 7 (Cánh diều 2024) có đáp án - Toán 7

Câu 7:

20/10/2024

Đơn giản biểu thức A = (1 - sin²x) .cot²x + (1 - cot²x) ta được :

A. sin²x

B. 2

C. 1

D. cot²x

Xem đáp án

Đáp án đúng: A.

* Phương pháp giải

- Áp dụng các công thức lượng giác cơ bản để biến đổi và giải:

sin2α + cos2α = 1

* Lời giải

* Lý thuyết và các dạng bài về giá trị lượng giác của một cung:

Các công thức lượng giác cơ bản:

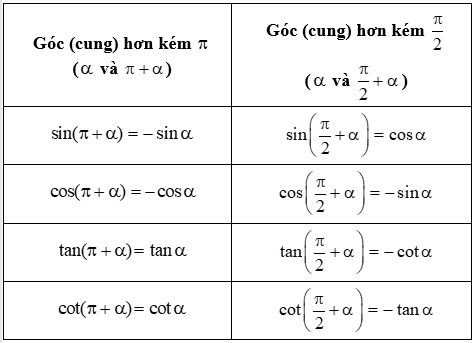
CÁC DẠNG BÀI:

Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị

Phương pháp giải:

Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.

Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác

Phương pháp giải:

Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.

Ta lựa chọn một trong các cách biến đổi sau:

* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)

* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.

* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.

Dạng 3: Rút gọn biểu thức lượng giác

Phương pháp giải:

Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.

Xem thêm các bài viết liên quan hay, chi tiết:

Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất

Trắc nghiệm Cung và góc lượng giác có đáp án – Toán lớp 10

Toán 10 Bài 2 giải SGK: Giá trị lượng giác của một cung

Câu 8:

22/07/2024

Biểu thức $A = \frac{\sin 515^{o} . \cos (- 475^{o}) + c o t 222^{o} . c o t 408^{o}}{c o t 415^{o} . c o t (- 505^{o}) + \tan 197^{o} . \tan 73^{o}}$ có kết quả rút gọn bằng

Xem đáp án

Chọn C.

Ta có :

Câu 9:

18/07/2024

Đơn giản biểu thức $A = \cos (\frac{π}{2} - α) + \sin (\frac{π}{2} - α) - \cos (\frac{π}{2} + α) - \sin (\frac{π}{2} + α)$ ta có :

A. A = 2sin α.

B. A = 2cos α.

C. A = sin α - cos α.

D. A = 0.

Xem đáp án

Thay vào biểu thức A ta được: A=2sin $α$ .

Chọn A.

Câu 10:

02/12/2024

Tính giá trị biểu thức P = sin²10⁰+ sin²20⁰+ sin²30⁰+ ..+ sin²80⁰

A. P = 1

B. P = 2

C. P = 4

D. P = 6

Xem đáp án

Đáp án đúng: C.

*Lời giải:

Ta có nhận xét sau:

10⁰+ 80⁰= 20⁰+ 70⁰= 30⁰+ 60⁰ = 40⁰+ 50⁰= 90⁰

nên các cung lượng giác tương ứng đôi một phụ nhau.

Do các góc phụ nhau thì sin góc này bằng cosin góc kia nên ta có:

P = (sin²10⁰+ sin²80⁰) + ( sin²20⁰+ sin²70⁰) + ...+ ( sin²40⁰+ sin²50⁰)

= (sin²10⁰+ cos²10⁰) + ( sin²20⁰+ cos²20⁰) + ...+ ( sin²40⁰+ cos²40⁰)

= 1 + 1 + 1 + 1= 4

*Phương pháp giải:

Áp dụng các công thức lượng giác sau để biến đổi biểu thức

* Lý thuyết và các dạng bài về góc và cung lượng giác:

Công thức nhân đôi:

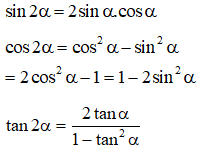
* Công thức hạ bậc:

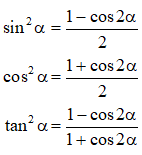
Phương trình lượng giác cơ bản

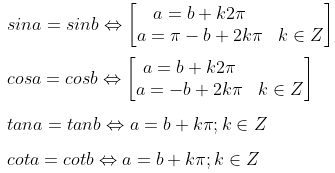
Phương trình lượng giác đặc biệt

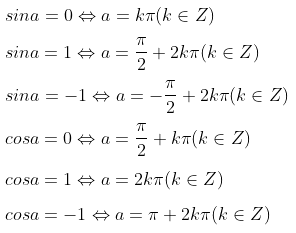
Hệ quả:

+) $\sin α, \cos α$ xác định với mọi giá trị của $α$ và $- 1 \leq \sin α \leq 1, - 1 \leq \cos α \leq 1$ .

+) $\tan α$ được xác định khi $α \neq \frac{π}{2} + k π$ , xác định khi $α \neq k π$

+) $\sin α = \sin (α + k 2 π), \cos α = \cos (α + k 2 π)$

$\tan α = \tan (α + k π), \cot α = \cot (α + k π)$

+) Dấu của các giá trị lượng giác phụ thuộc vào vị trí điểm M nằm trên đường tròn lượng giác.

Ta có bảng xác định dấu của các giá trị lượng giác:

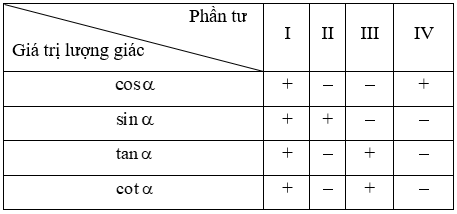
Xem thêm các bài viết liên quan hay, chi tiết:

Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất

Giải Toán 10 Chương 6: Cung và góc lượng giác. Công thức lượng giác

Trắc nghiệm Cung và góc lượng giác (có đáp án)

Câu 11:

27/10/2024

Rút gọn biểu thức $A = \frac{2 \cos^{2} x - 1}{\sin x + \cos x}$

A. A = cosx + sinx.

B. A = cos x - sinx.

C. A = sinx - cosx.

D. A = -sinx - cosx.

Xem đáp án

Đáp án đúng: B.

* Lời giải:

Ta có:

* Phương pháp giải:

- sử dụng công thức lượng giác cở bản để biến đổi biểu thức, rút gọn tử và mẫu: $\sin^{2} x + \cos^{2} x = 1$

* Lý thuyết và các dạng bài về góc và cung lượng giác:

Công thức nhân đôi:

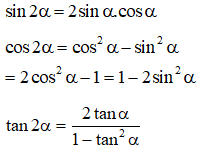
* Công thức hạ bậc:

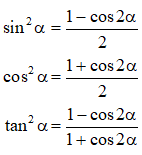
Phương trình lượng giác cơ bản

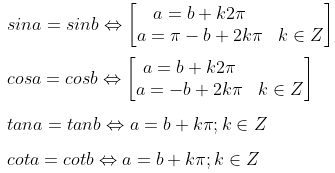
Phương trình lượng giác đặc biệt

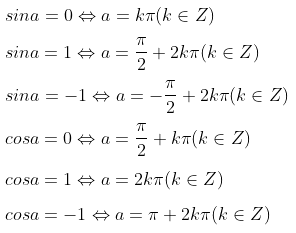
Xem thêm các bài viết liên quan hay, chi tiết:

Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất

Giải Toán 10 Chương 6: Cung và góc lượng giác. Công thức lượng giác

Trắc nghiệm Cung và góc lượng giác (có đáp án)

Câu 12:

23/07/2024

Cho P = sin(π + α).cos(π - α) và $Q = \sin (\frac{π}{2} - α) . \cos (\frac{π}{2} + α)$ .Mệnh đề nào dưới đây là đúng ?

A. P – Q = 1

B. P + Q = 2

C. P + Q = 0

D. P – Q = 0

Xem đáp án

Chọn C.

Ta có :

P = sin(π + α).cos(π - α) = -sin α.(-cos α) = sin α.cos α.

Và = cos α.(-sin α) = -sin α.cos α.

Do đó; P + Q = 0.

Câu 13:

19/09/2024

Biết A ; B ; C là các góc của tam giác ABC , mệnh đề nào sau đây đúng:

A. sin( A + C) = - sinB

B. cos( A + B) = - cos C

C. tan (A + C) = tanB

D. cot( A+ C) = cot B

Xem đáp án

Chọn B.

Tổng số đo 3 góc của 1 tam giác là π nên A + B + C = π

Suy ra : A + B = π - C

Do đó cos(A + B) = cos( π - C) = -cosC.

* Lý thuyết liên quan

1. Định lí Côsin

Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

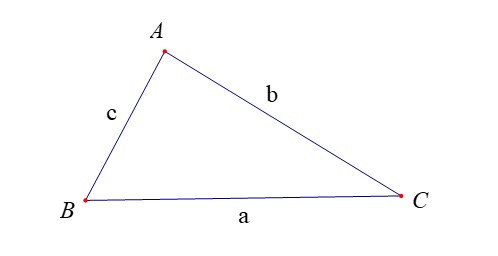
Định lí Côsin. Trong tam giác ABC:

a² = b² + c² – 2bc.cosA.

b² = c² + a² – 2ca.cosB.

c² = a² + b² – 2ab.cosC.

2. Định lí sin

Trong tam giác ABC: $\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2 R$ .

Câu 14:

23/07/2024

Cho tam giác ABC. Hãy tìm hệ thức sai:

A. sinA = -sin( 2A + B + C)

B. $\sin A = - \cos \frac{3 A + B + C}{2}$

C. $\cos C = \sin \frac{A + B + 3 C}{2}$

D. sin C = sin( A + B + 2C)

Xem đáp án

Chọn D.

Do A; B; C là ba góc của một tam giác nên A + B + C = 180⁰

Suy ra: A + B= 180⁰- C nên A + B + 2C = 180⁰+ C

Ta có : sin( A + B + 2C) = sin( 180⁰+ C) = - sinC.

Câu 15:

23/07/2024

Cho $7 π < α < \frac{15 π}{2}$ . Xác định dấu của biểu thức $M = \sin α . \tan (\frac{π}{2} + α)$

A. M ≥ 0

B. M < 0

C. M > 0

D. M ≤ 0

Xem đáp án

Chọn C.

Ta có ; 7π = 2.3π + π và ; do đó góc đang xét nằm trong góc phần tư thứ ba.

Suy ra ; sinα < 0 và .

Vậy

Câu 16:

07/12/2024

Tính giá trị của $\cos [\frac{π}{3} + (2 k + 1) π]$

Xem đáp án

Đáp án đúng là C.

Lời giải

=

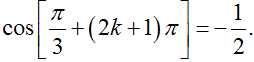
*Phương pháp giải:

- thu gọn trong ngoặc lại trước.

- Rồi dùng: góc(cung) hơn kém $π$ : cos( $π + α)$ = $- \cos α$

*Lý thuyết

Các công thức lượng giác cơ bản:

CÁC DẠNG BÀI:

Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị

Phương pháp giải:

Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.

Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác

Phương pháp giải:

Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.

Ta lựa chọn một trong các cách biến đổi sau:

* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)

* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.

* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.

Dạng 3: Rút gọn biểu thức lượng giác

Phương pháp giải:

Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.

Xem thêm

Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất

Trắc nghiệm Cung và góc lượng giác có đáp án – Toán lớp 10

cos(π3+(2k+1)π)=cos(π3+π)=−cosπ3=−12

Câu 17:

19/07/2024

Cho góc α thỏa mãn $\sin α = \frac{3}{5} v à \frac{π}{2} < α < π$ .Tính $P = \frac{\tan α}{1 + \tan^{2} α}$

A. $P = \frac{9}{25}$

B. $P = \frac{3}{25}$

C. $P = \frac{14}{25}$

D. $P = - \frac{12}{25}$

Xem đáp án

Chọn D.

Ta có suy ra :

Thay vào P ta được

Câu 18:

17/07/2024

Cho góc α thỏa mãn tanα = 2. Tính $P = \frac{2 \sin^{2} α + 3 \sin α . \cos α + 4 \cos^{2} α}{5 \sin^{2} α + 6 \cos^{2} α}$

A. $P = \frac{9}{13}$

B. $P = \frac{9}{65}$

C. $P = \frac{12}{13}$

D. $P = \frac{8}{13}$

Xem đáp án

Chọn A.

Chia cả tử và mẫu của P cho cos²α ta được

Câu 19:

22/07/2024

Tính giá trị của biểu thức A = sin⁶x + cos⁶x + 3sin²xcos²x.

A. A = 1

B. A = 2

C. A = 3

D. A = 4

Xem đáp án

Đáp án A.

Câu 20:

23/07/2024

Cho $\sin a + \cos a = \frac{5}{4}$ . Khi đó sina.cos a có giá trị bằng

A. 1

B. $\frac{9}{32}$

C. $\frac{3}{16}$

D. $\frac{5}{4}$

Xem đáp án

Chọn B.

Ta có

Câu 21:

17/07/2024

Cho cota = 3. Khi đó $\frac{3 \sin a - 2 c o s a}{12 \sin^{3} a + 4 \cos^{3} a}$ có giá trị bằng

A. $- \frac{1}{4}$

B. $- \frac{5}{4}$

C. $\frac{3}{4}$

D. $\frac{1}{4}$

Xem đáp án

Chọn A.

Câu 22:

06/01/2025

Cho tana + cota = m. Khi đó cot³a + tan³a có giá trị bằng

A. m³+ 3m

B. m³- 3m

C. 3m³+ m

D. 3m³+ 3m

Xem đáp án

Đáp án đúng là B.

Lời giải

Ta có cot³a + tan³a = ( tan a + cota) ³- 3tan a.cot a ( cot a + tan a)

= m³- 3.1.m = m³- 3m

*Phương pháp giải:

+ Tách một hạng tử thành tổng ( hiệu ) nhiều hạng tử, rồi nhóm các hạng tử thích hợp để xuất hiện nhân tử chung.

+ Hoặc thêm ( bớt) cùng 1 hạng tử, nhóm các hạng tử thích hợp để xuất hiện nhân tử chung.

*Lý thuyết:

- Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

- Phương pháp đặt nhân tử chung là một phương pháp để phân tích đa thức thành nhân tử bằng cách nhóm các hạng tử có chung nhân tử:

A.B + A.C = A.(B + C)

Dạng 1: Phân tích đa thức thành nhân tử:

a. Phương pháp giải:

Phân tích các hạng tử của đa thức để chọn nhân tử chung thích hợp, sau đó áp dụng tính chất phân phối của phép nhân với phép cộng

2. Dạng 2: Các bài toán liên quan

a. Phương pháp giải:

Phân tích các hạng tử của đa thức để chọn nhân tử chung thích hợp, sau đó áp dụng tính chất phân phối của phép nhân với phép cộng để làm một số bài toán tính nhanh, tính giá trị biểu thức, tìm x,…

3. Dạng 3: Chứng minh các bài toán số nguyên:

a. Phương pháp giải:

Phân tích các biểu thức đã cho một cách hợp lí thành các tích và sử dụng tính chất chia hết của số nguyên.

Xem thêm

200 bài tập về những hằng đẳng thức đáng nhớ (có đáp án ) và cách giải

Các phương pháp phân tích đa thức thành nhân tử, bài tập và cách giải () – Toán 8

Câu 23:

17/07/2024

Kết quả rút gọn của biểu thức ${(\frac{\sin a + \tan a}{c o s a + 1})}^{2} + 1$ bằng

A. cos²a

B. tan²a

C. $\frac{1}{\cos^{2} a}$

D. $\frac{1}{\sin^{2} a}$

Xem đáp án

Chọn C.

Ta có

Câu 24:

18/07/2024

Đẳng thức nào trong các đẳng thức sau là sai.

Xem đáp án

Chọn C.

Ta xét các phương án:

suy ra A đúng

+ Tương tự ta có B đúng.

nên D đúng.

nên C sai.

Câu 25:

18/07/2024

Rút gọn biểu thức $A = \frac{\cos^{2} x - \sin^{2} x}{c o t^{2} x - \tan^{2} x}$ ta được.

A. $A = - \frac{1}{4} \sin^{2} 2 x$

B. $A = \frac{1}{4} \sin^{2} 2 x$

C. $A = \frac{1}{4} c o s^{2} 2 x$

D. A = cos²2x

Xem đáp án

Chọn B.

Ta có:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3