200 bài tập về những hằng đẳng thức đáng nhớ (có đáp án 2024) và cách giải
Với cách giải các dạng toán về những hằng đẳng thức đáng nhớ lớp 8 môn Toán lớp 8 Đại số gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về những hằng đẳng thức đáng nhớ lớp 8 lớp 8. Mời các bạn đón xem:
Những hằng đẳng thức đáng nhớ lớp 8 và cách giải các dạng bài tập
A. Bình phương của một tổng, bình phương của một hiệu và hiệu hai bình phương
I. Lý thuyết
1. Bình phương của một tổng
2. Bình phương của một hiệu
3. Hiệu hai bình phương
= (A – B)(A + B)
II. Các dạng bài
Dạng 1: Thực hiện phép tính
a. Phương pháp giải:
Sử dụng trực tiếp các hằng đẳng thức đã học để khai triển các biểu thức
b, Ví dụ minh họa:
VD1: Thực hiện phép tính:
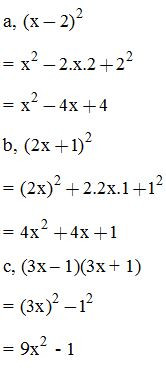
VD2: Viết các biểu thức sau dưới dạng bình phương một tổng hoặc bình phương một hiệu:
a,
b,
Giải:
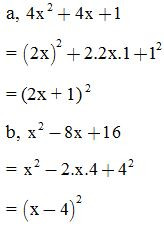
Dạng 2: Chứng minh các đẳng thức
a. Phương pháp giải:
Áp dụng linh hoạt các hằng đẳng thức, lựa chọn vế có thể dễ dàng áp dụng các hằng đẳng thức.
b. Ví dụ minh họa:
Chứng minh các đẳng thức sau:
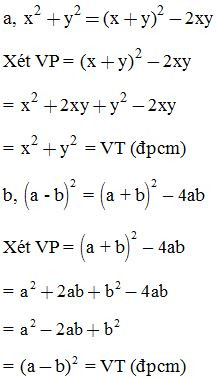
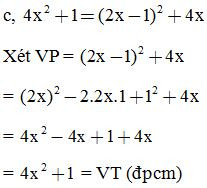
Dạng 3: Tính nhanh
a. Phương pháp giải:
Áp dụng linh hoạt các hằng đẳng thức cho các số tự nhiên
b. Ví dụ minh họa:
Tính nhanh:
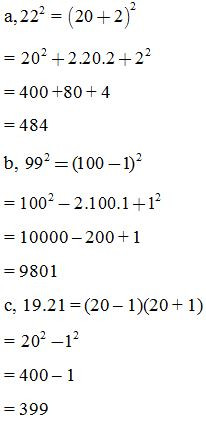
Dạng 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
a. Phương pháp giải:
Sử dụng các hằng đẳng thức và cần chú ý:
và
b. Ví dụ minh họa:
a, Chứng minh luôn dương với mọi x
Giải:
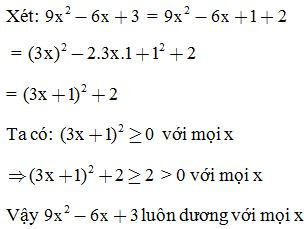
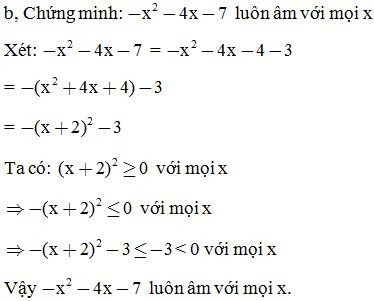
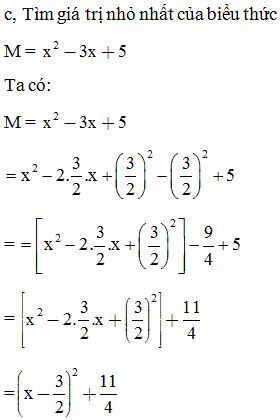
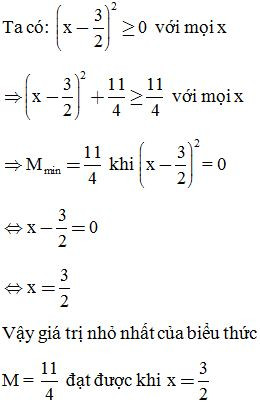
B. Lập phương của một tổng hoặc một hiệu
I. Lý thuyết
4. Lập phương của một tổng
5. Lập phương của một hiệu
II. Các dạng bài
Dạng 1: Sử dụng hằng đẳng thức để khai triển và rút gọn biểu thức và tính giá trị biểu thức
a. Phương pháp giải:
Sử dụng hằng đẳng thức đã học để khai triển và rút gọn biểu thức.
b. Ví dụ minh họa:
VD1: Thực hiện phép tính:
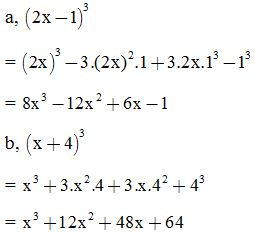
VD2: Rút gọn biểu thức:
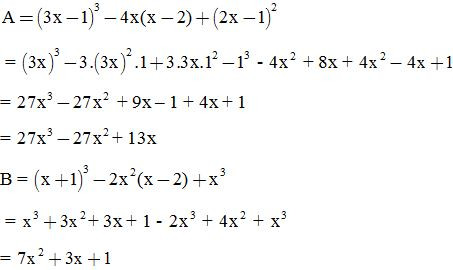
VD3: Viết các biểu thức sau dưới dạng lập phương một tổng hoặc lập phương một hiệu:
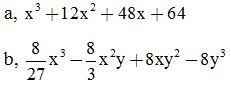
Giải:
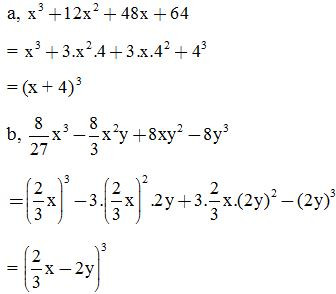
VD4: Tính giá trị các biểu thức sau:
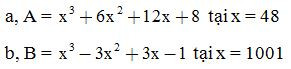
Giải:
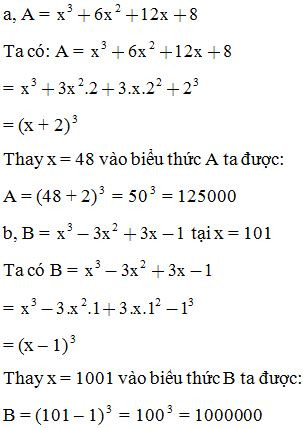
Dạng 2: Sử dụng hằng đẳng thức để tính nhanh
a. Phương pháp giải:
Sử dụng linh hoạt các hằng đẳng thức để tính nhanh
b. Ví dụ minh họa:
Tính nhanh:
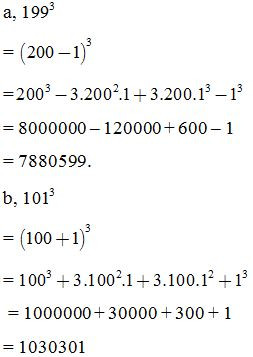
C. Tổng hoặc hiệu hai lập phương
I. Lý thuyết
6. Tổng hai lập phương
7. Hiệu hai lập phương
II. Các dạng bài
Dạng 1: Sử dụng hằng đẳng thức để rút gọn và khai triển biểu thức
a. Phương pháp giải:
Sử dụng các hằng đẳng thức đã học để khai triển hoặc rút gọn biểu thức.
b. Ví dụ minh họa:
VD1: Thực hiện phép tính:
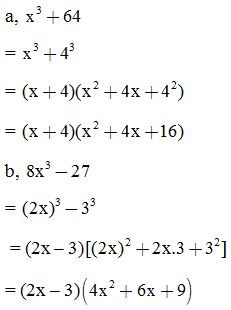
VD2: Rút gọn biểu thức:
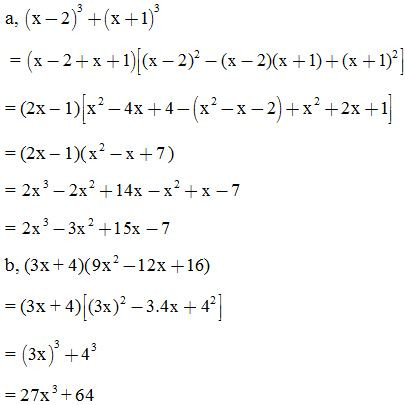
Dạng 2: Sử dụng hằng đẳng thức để tính nhanh
a, Phương pháp giải:
Sử dụng các hằng đẳng thức đã học để phân tích và tính
Chú ý thêm:
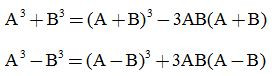
b, Ví dụ minh họa:
Tính nhanh:
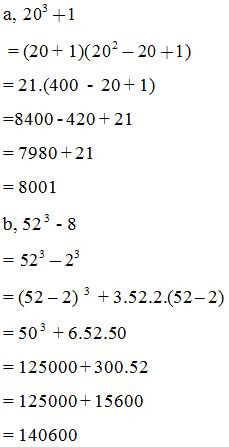
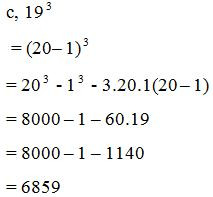
III. Bài tập vận dụng
Bài 1: Thực hiện phép tính:
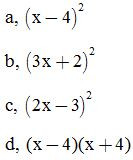
ĐS:
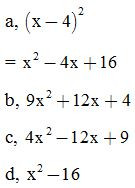
Bài 2: Thực hiện phép tính:
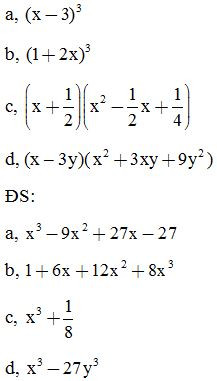
Bài 3: Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:
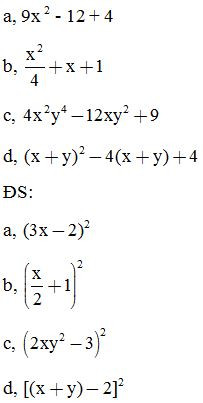
Bài 4: Chứng minh các đẳng thức sau:
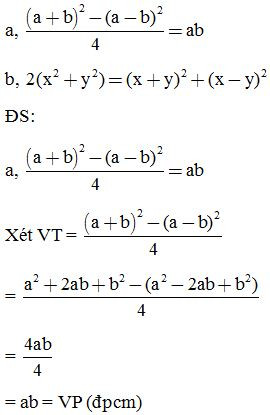
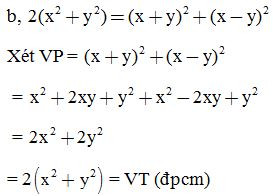
Bài 5: Rút gọn biểu thức:
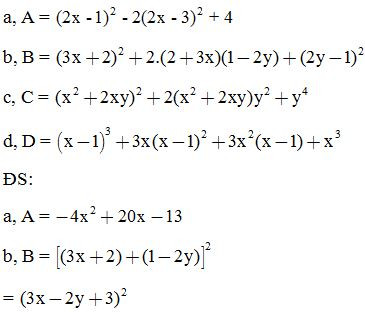
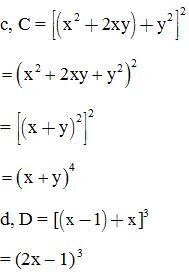
Bài 6: Rút gọn biểu thức:
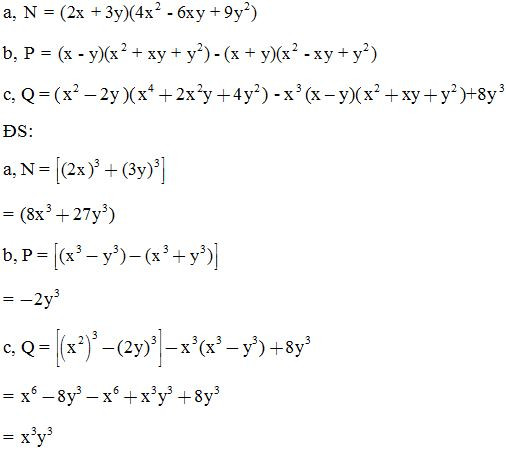
Bài 7: Tính giá trị của các biểu thức sau:
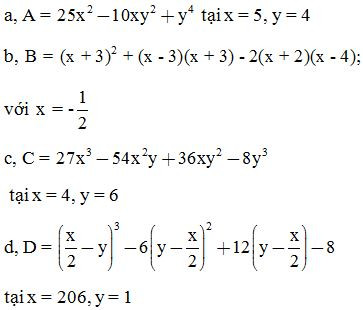
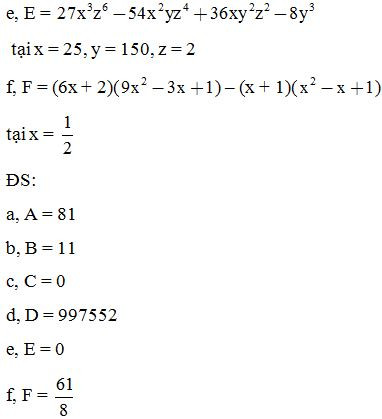
Bài 8: Tính nhanh:
a, 292
b, 62.58
c, 1022
d, 1013
e, 913 + 3.912 .9 + 3.91.92 + 93
f, 183 - 3.182 .8 + 3.18.82 - 2
g, 183+23
h, 233 - 27
ĐS:
a, 292
= (30 – 1)2
= 841
b, 62.58
= (60 + 2)(60 – 2)
= 602 - 22
= 3596
c, 1022
= (100 + 2)2
= 10404
d, 1013
= (100 + 1)3
= 1030301
e, 913 + 3.912 .9 + 3.91.92 + 93
= (91 + 9)3
= 1003
= 1000000
f, 183 - 3.182 .8 + 3.18.82 - 29
= (18 – 8)3
= 103
= 1000
g, 183 + 23
= (18 + 2)3 – 3.18.2(18 + 2)
= 203 - 6.18.20
= 5840
h, 233 - 27
= 233 - 33
= (23 – 3)3 + 3.23.3.(23 – 3)
= 203 + 9.23.20
= 12140
Bài 9: Tính giá trị biểu thức:
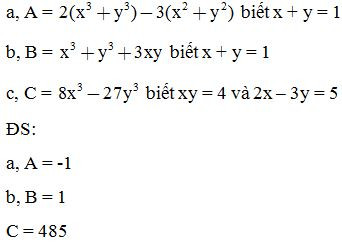
Bài 10: Chứng minh các biểu thức sau không phụ thuộc vào giá trị của biến x:
a, A =3(x – 1)2 - (x + 1)2 + 2(x – 3)(x + 3) – (2x + 3)2 - (5 – 20x)
b, B = -x(x + 2)2 + (2x + 1)2 + (x + 3)(x2 - 3x + 9) – 1
ĐS:
a, A = - 30
b, B = 27
Bài 11: Tính giá trị nhỏ nhất của biểu thức:
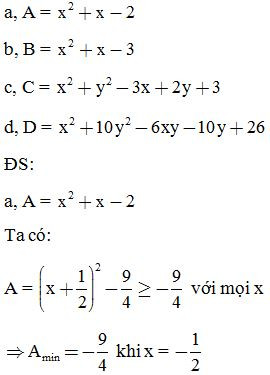
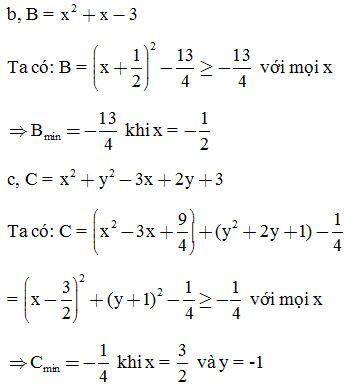
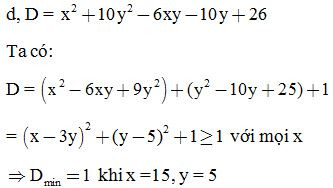
Bài 12: Tìm giá trị lớn nhất của biểu thức:
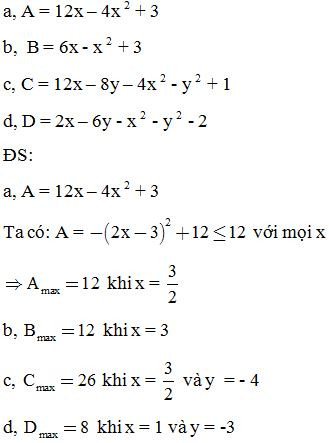
Bài 13: Chứng minh rằng với mọi a, b, c ta luôn có:
(a + b + c)3 = a3 + b3 + c3 + 3(a + b)(b + c)(c + a)
ĐS: Hướng dẫn:
Đặt a + b = A, B = c
Ta có: VT = (a + b + c)3
= (A + B)3 = A3 + B + 3A2B + 3AB2
Thay vào ta được:
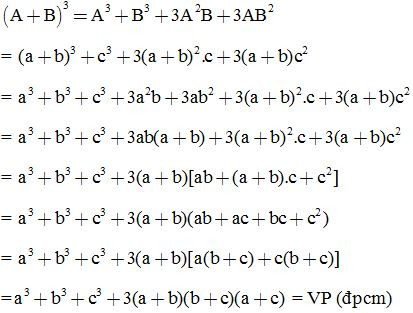
Xem thêm các dạng bài tập Toán lớp 8 có đáp án và lời giải chi tiết khác:
Các phương pháp phân tích đa thức thành nhân tử chi tiết nhất
Cách chia đơn thức cho đơn thức, chia đa thức cho đơn thức chi tiết
Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải
Góc trong tứ giác và cách giải các dạng bài tập
Hình thang, hình thang vuông, hình thang cân lớp 8 và cách giải
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8