50 bài tập về diện tích hình thang (có đáp án 2024) – Toán 8

Diện tích hình thang và cách giải bài tập - Toán lớp 8

I. Lý thuyết

1. Công thức tính diện tích hình thang

- Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao

$S=\frac{1}{2}\left(a+b\right).h$ trong đó: a, b là độ dài hai đáy, h là độ dài đường cao.

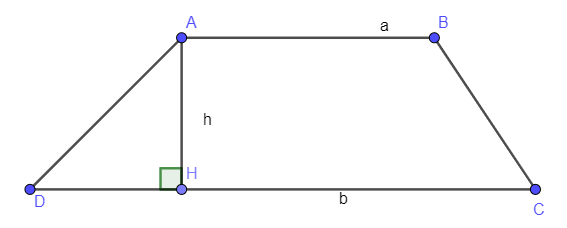
Cho hình thang ABCD có AB // CD, AB = a, DC = b. Đường cao AH = h. Khi đó:

$S_{ABCD}=\frac{1}{2}\left(AB+CD\right)AH=\frac{1}{2}\left(a+b\right).h$

2. Diện tích hình bình hành

Diện tích hình bình hành bằng tích của một cạnh nhân với chiều cao ứng với cạnh đó

S = a.h với a là độ dài đáy, h là độ dài chiều cao tương ứng.

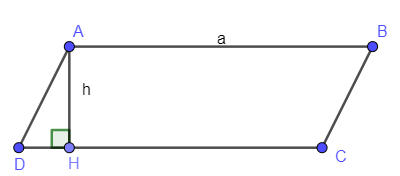
Cho hình bình hành ABCD có CD = a, đường cao AH = h. Diện tích hình bình hành là:

$S_{ABCD}=CD.AH=a.h$

II. Dạng bài tập

Dạng 1: Tính diện tích hình thang

Phương pháp giải: Sử dụng công thức tính diện tích hình thang

trong đó: a, b là độ dài hai đáy, h là đường cao.

Ví dụ 1: Tính diện tích hình thang ABCD biết $\widehat{A}=\widehat{D}=90°$ ,$\widehat{C}=45°$, AB = 1cm, DC = 3cm.

Lời giải:

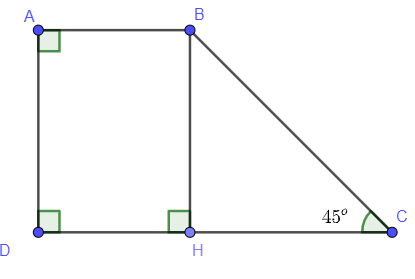
Vẽ $BH\perp CD$ tại H, BH là đường cao của hình thang ABCD$\Rightarrow \widehat{BHD}=90°$

Xét tứ giác ABHD có:

$\widehat{A}=\widehat{D}=\widehat{BHD}=90°$

$\Rightarrow$Tứ giác ABHD là hình chữ nhật (Dấu hiệu nhận biết)

$\Rightarrow$AB = DH = 1cm

Lại có:

CD = DH + HC

$\iff$3 = 1 + HC

$\Rightarrow$HC = 3 – 1 = 2cm

Xét tam giác BHC vuông tại H ta có: $\widehat{C}=45°$(giả thuyết)

$\Rightarrow$tam giác BHC là tam giác vuông cân tại H (dấu hiệu nhận biết tam giác vuông cân)

$\Rightarrow$BH = HC = 2cm (tính chất)

Diện tích hình thang ABCD là:

$S_{ABCD}=\frac{1}{2}\left(AB+CD\right).BH=\frac{1}{2}\left(1+3\right).2=4c{m}^2$.

Ví dụ 2: Cho hình thang cân ABCD có AB // CD và AB < CD. Kẻ đường cao AH. Biết AH = 8cm, HC = 12cm. Tính diện tích hình thang ABCD.

Lời giải:

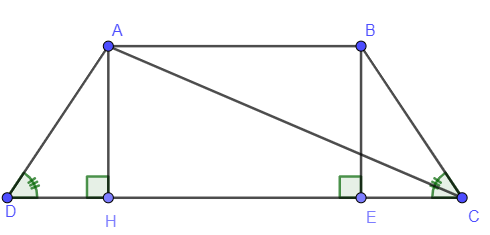
Kẻ BE vuông góc với DC tại E$\Rightarrow \widehat{BEC}=90°$

Vì AH là đường cao của hình thang nên AH vuông góc với DC$\Rightarrow \widehat{AHD}=90°$

Ta có: AH và BE cùng vuông góc với CD nên AH // BE (quan hệ từ vuông góc đến song song)

Vì ABCD là hình thang cân $\Rightarrow \left\{\begin{array}{l}AD=BC\\ \widehat{ADH}=\widehat{BCE}\end{array}\right.$ (tính chất)

Xét tứ giác ABEH có:

AB // HE (do ABCD là hình thang)

AH // BE (chứng minh trên)

Do đó tứ giác ABEH là hình bình hành.

$\Rightarrow$HE = AB (tính chất)

Xét tam giác AHD và tam giác BEC có:

$\widehat{AHD}=\widehat{BEC}=90°$ (chứng minh trên)

$\widehat{ADH}=\widehat{BCE}$ (chứng minh trên)

$AD=BC$ (chứng minh trên)

Do đó $\Delta AHD=\Delta BEC$ (cạnh huyền – góc nhọn)

$\Rightarrow$DH = EC (hai cạnh tương ứng)

Đặt DH = EC = x (0 < x < 12)

Khi đó: HE = HC – EC = 12 – x

Ta có: AB + DC = HE + DH + HE + EC (do AB = HE đã chứng minh ở trên)

$\Rightarrow$AB + DC = 12 – x + x + 12 – x + x = 24cm

Diện tích hình thang ABCB là:

$S_{ABCD}=\frac{1}{2}\left(AB+CD\right)AH=\frac{1}{2}\mathrm{.24.8}=96c{m}^2$.

Dạng 2: Tính diện tích hình bình hành

Phương pháp giải: Sử dụng công thức tính diện tích hình bình hành

Diện tích hình bình hành bằng tích của một cạnh nhân với chiều cao ứng với cạnh đó

S = a.h

Ví dụ 1: Cho hình bình hành ABCD với cạnh $AB=10\sqrt{3}cm$ , AD = 8cm, $\widehat{A}=60°$. Tính diện tích hình bình hành.

Lời giải:

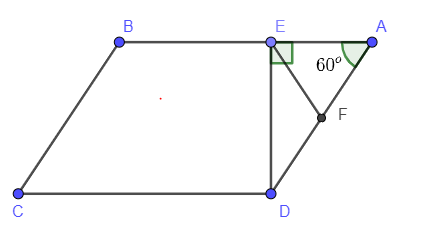
Kẻ DE vuông góc với AB tại E, DE là đường cao của hình bình hành ABCD ứng với cạnh AB$\Rightarrow \widehat{DEA}=90°$

Gọi F là trung điểm của AD.

Xét tam giác AED vuông tại E ta có:

EF là đường trung tuyến

$\Rightarrow E\text{}F=FA=\frac{1}{2}DA$(định lý đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

$\Rightarrow$tam giác AFE cân tại F, mà góc $\widehat{A}=60°$ $\Rightarrow$tam giác AFE là tam giác đều (đấu hiệu nhận biết)

AF = EF = EA =$\frac{1}{2}DA$ = 4cm

Xét tam giác DEA vuông tại E ta có:

$E{A}^2+E{D}^2=A{D}^2$(định lý Py – ta – go)

$\iff 4^2+E{D}^2=8^2$

$\iff E{D}^2=64-16$

$\iff E{D}^2=48$

$\Rightarrow ED=4\sqrt{3}$cm

Diện tích hình bình hành ABCD là:

$S_{ABDC}=AB.DE=10\sqrt{3}.4\sqrt{3}=120c{m}^2$

Ví dụ 2: Cho hình bình hành ABCD. Có diện tích là S. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Tính diện tích tứ giác MNDC theo S.

Lời giải:

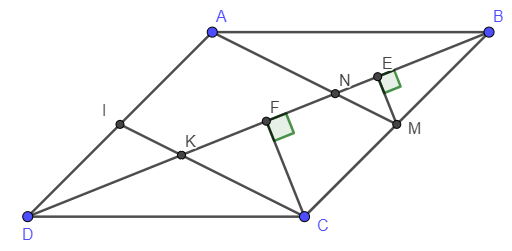
Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ ME vuông góc với BD tại E, kẻ CF vuông góc với BD tại F.

Vì I là trung điểm của AD nên AI = DI = $\frac{1}{2}$ AD

Vì M là trung điểm của BC nên BM = MC = $\frac{1}{2}$ BC.

Mà ABCD là hình bình hành nên AD = BC

Do đó AI = CM

Lại có AD // CB nên AI song song với CM

Xét tứ giác AICM có:

AI = CM

AI // CM

Do đó: tứ giác AICM là hình bình hành.

Nên CI // AM (tính chất)

Vì CI // AM nên IK // AN

Xét tam giác DAN có:

KI // AN

I là trung điểm của AN

Do đó: K là trung điểm của DN

$\Rightarrow KD=KN$(1)

Chứng minh tương tự ta được N là trung điểm của BK

$\Rightarrow KN=NB$(2)

Từ (1) và (2) $\Rightarrow$ KD = KN = NB

$\Rightarrow BN=\frac{1}{3}BD$(Do BD = KD + KN + NB) (3)

Vì ME vuông góc với BD, CF vuông góc với DB nên ME // CF.

Xét tam giác BFC có:

ME // CF

M là trung điểm của BC nên E là trung điểm của BF

$\Rightarrow$ME là đường trung bình của tam giác BFC (định lý đường trung bình trong tam giác).

$\Rightarrow ME=\frac{1}{2}CF$(4)

Ta có:

$S_{BDC}=\frac{1}{2}CF.BD$

$S_{MNB}=\frac{1}{2}ME.NB$

Tỉ số diện tích của tam giác BDC và tam giác MNB là:

$\frac{S_{BDC}}{S_{MNB}}=\frac{\frac{1}{2}CF.BD}{\frac{1}{2}ME.NB}=\frac{\frac{1}{2}CF.BD}{\frac{1}{2}.\frac{1}{2}CF.\frac{1}{3}BD}$ (do (3) và (4))

$\frac{S_{BDC}}{S_{MNB}}=6$

$\Rightarrow S_{BDC}=6S_{MNB}$

Mà $S_{BDC}=S_{NMCD}+S_{MNB}=6S_{MNB}$

$\Rightarrow S_{NMCD}=5S_{MNB}$

$\Rightarrow S_{NMCD}=\frac{5}{6}{S}_{BDC}$

Mà $S_{BDC}=\frac{1}{2}{S}_{ABCD}$ (do ABCD là hình bình hành)

$\Rightarrow S_{NMCD}=\frac{5}{6}{S}_{BDC}=\frac{5}{6}.\frac{1}{2}{S}_{ABCD}=\frac{5}{12}{S}_{ABCD}$

Hay $S_{NMCD}=\frac{5}{12}S$

III. Bài tập vận dụng

Bài 1: Cho hình thang ABCD vuông tại A và D, AB = 3cm, BC = 5cm, CD = 6cm. Tính diện tích hình thang.

Bài 2: Cho hình thang cân ABCD cân (AB // CD; AB < CD) . Biết AB = 10cm, CD = 20cm, AD = 13cm. Tính diện tích hình thang ABCD.

Bài 3: Tính các góc của hình bình hành ABCD có diện tích là 30 $c{m}^2$, AB = 10cm, AD = 6cm, góc A lớn hơn góc D.

Bài 4: Cho hình bình hành ABCD. Gọi P, Q, R, S lần lượt là trung điểm của các cạnh CD, DA, AB, BC. Đoạn DR cắt CQ, CA, SA theo thứ tự tại H, I, G. Đoạn BP cắt SA, AC, CQ theo thứ tự tại F, J, E. Chứng minh:

a) Tứ giác EFGH là hình bình hành.

b) AI = IJ = JC.

c) $S_{EFCH}=\frac{1}{5}{S}_{ABCD}$ .

Bài 5: Cho hình thang ABCD có hai đáy AB = 5cm, CD = 15cm và hai đường chéo là AC = 16cm, BD = 12cm. Tính diện tích hình thang ABCD.

Bài 6: Cho hình bình hành ABCD, M là trung điểm của AD, qua M kẻ đường thẳng d cắt AB, CD lần lượt tại E và F. Kẻ MH vuông góc với BC tại H. Chứng minh: $S_{EBCF}=MH.BC$

Bài 7: Cho hình thang ABCD (AB // CD), E là trung điểm của AD. Đường thẳng qua E và song song với BC cắt AB và CD ở I và K. Chứng minh:$S_{ABCD}=S_{BIKC}$

Bài 8: Cho hình thang ABCD có đáy AD = 4cm, đường trung bình bằng 5cm. Tính diện tích lớn nhất của hình thang.

Bài 9: Cho hình thang ABCD (AB // CD) và AB < CD. Xác định R và S lần lượt trên các cạnh AB, CD sao cho $S_{ARSD}=3S_{BCSR}$.

Bài 10: Cho hình thang ABCD (AB // CD) có AB = 2cm, BC = 8cm, CD = 9cm và $\widehat{C}=30°$ . Tính diện tích hình thang ABCD.

Xem thêm các dạng bài tập Toán lớp 8 có đáp án và lời giải chi tiết khác:

Diện tích hình thoi và cách giải bài tập

Diện tích đa giác và cách giải bài tập

Đa giác, Đa giác lồi, Đa giác đều và cách giải bài tập

Diện tích hình chữ nhật và cách giải bài tập

Diện tích tam giác và cách giải bài tập