50 bài tập về diện tích tam giác (có đáp án 2024) – Toán 8

Diện tích tam giác và cách giải bài tập - Toán lớp 8

I. Lý thuyết

+ Tam giác thường:

Diện tích tam giác bằng nửa tích một cạnh với chiều cao tương ứng.

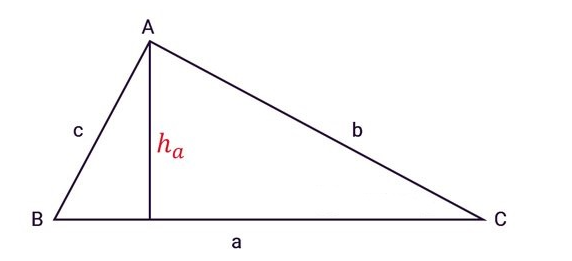
S = $\frac{1}{2}a.h_a$ (đơn vị diện tích)

Với a là độ dài cạnh BC;$h_a$ là độ dài đường cao tương ứng với cạnh BC.

+ Tam giác vuông

Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông

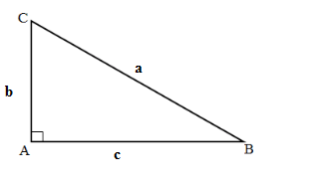
Cho tam giác ABC vuông tại A có AB = c; AC = b

Diện tích tam giác vuông ABC: S = $\frac{1}{2}bc$ (đơn vị diện tích).

Chú ý:

- Nếu hai tam giác có một cạnh bằng nhau thì tỉ số diện tích hai tam giác đó bằng tỉ số hai đường cao tương ứng với hai cạnh đó.

- Nếu hai tam giác có một đường cao bằng nhau thì tỉ số diện tích hai tam giác đó bằng tỉ số các cạnh tương ứng.

II. Dạng bài tập

Dạng 1: Tính diện tích tam giác và chứng minh hệ thức về diện tích tam giác

Phương pháp giải: Sử dụng công thức tính diện tích tam giác

+ Đối với tam giác thường.

S = $\frac{1}{2}a.h_a$ (đơn vị diện tích)

Với a là độ dài cạnh; là độ dài đường cao tương ứng.

+ Đối với tam giác vuông

S = $\frac{1}{2}bc$ (đơn vị diện tích)

Với b, c là độ dài hai cạnh góc vuông.

Ví dụ 1: Cho tam giác ABC và đường trung tuyến AM. Chứng minh .

Lời giải:

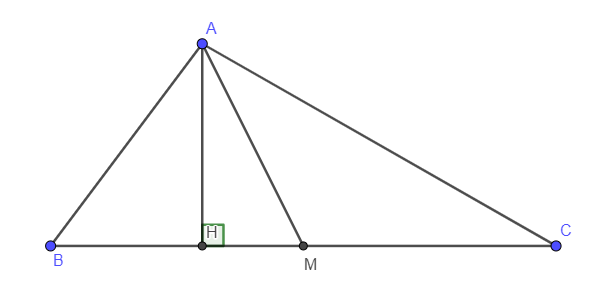
Ta có: M là trung điểm của BC nên BM = CM

Kẻ AH $\perp$ BC tại H

Xét tam giác ABM có: AH $\perp$ BC $\Rightarrow$ AH$\perp$ BM nên AH là đường cao của tam giác ABM.

Diện tích tam giác ABM là

$S_{AMB}=\frac{1}{2}AH.BM$(đơn vị diện tích) (1)

Xét tam giác AMC có: AH $\perp$ BC $\Rightarrow$ AH$\perp$CM nên AH là đường cao của tam giác ACM.

$S_{AMC}=\frac{1}{2}AH.CM$(2)

Từ (1) và (2) kết hợp với BM = CM$\Rightarrow$ $S_{AMB}$ = $S_{AMC}$

Ví dụ 2: Tính diện tích tam giác cân có độ dài cạnh bên là a độ dài cạnh đáy là b theo a, b.

Lời giải:

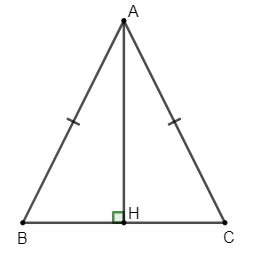
Giả sử tam giác cân cần tính diện tích là tam giác ABC cân tại A với AB = AC = a; BC = b

Gọi H là chân đường cao hạ từ A xuống BC. Vì tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến nên H là trung điểm của BC

$\Rightarrow$BH = CH = $\frac{1}{2}$BC = $\frac{1}{2}$b

Xét tam giác AHB vuông tại H ta có:

$A{B}^2=A{H}^2+B{H}^2$(định lý Py – ta – go)

$\iff a^2=A{H}^2+{\left(\frac{b}{2}\right)}^2$

$\iff A{H}^2=a^2-\frac{b^2}{4}$

$\Rightarrow AH=\sqrt{a^2-\frac{b^2}{4}}$$=\sqrt{\frac{4a^2-b^2}{4}}=\frac{\sqrt{4a^2-b^2}}{2}$

Diện tích tam giác ABC là

$S=\frac{1}{2}AH.BC=\frac{1}{2}\frac{\sqrt{4a^2-b^2}}{2}.b=\frac{b\sqrt{4a^2-b^2}}{4}$

Dạng 2: Sử dụng công thức diện tính tích tam giác để tính độ dài các đoạn thẳng, chứng minh hệ thức hình học

Phương pháp giải:

+ Từ công thức $S=\frac{1}{2}ah$ ta suy ra công thức $h=\frac{2S}{a}$ và $a=\frac{2S}{h}$

a, h là độ dài đáy và chiều cao tương ứng.

+ Phát hiện quan hệ diện tích trong hình rồi sử dụng các công thức trên.

Ví dụ 1: Cho tam giác ABC cân tại A. Có BC = 60cm. Đường cao AH = 40cm. Tính các đường cao BE và CF của tam giác.

Lời giải:

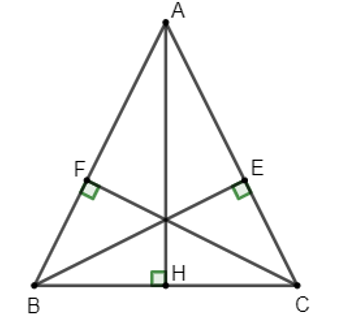
Vì tam giác ABC là tam giác cân tại A nên AH vừa là đường cao, vừa là đường trung tuyến trong tam giác nên H là trung điểm BC

$\Rightarrow BH=CH=\frac{BC}{2}=\frac{60}{2}=30cm$

Xét tam giác ABH vuông tại H ta có:

$A{B}^2=A{H}^2+B{H}^2$(định lý Py – ta – go)

$\iff A{B}^2={40}^2+{30}^2$

$\iff A{B}^2=1600+900$

$\iff A{B}^2=2500$

$\Rightarrow AB=50cm$

Mà tam giác ABC là tam giác cân

$\Rightarrow AB=AC=50cm$

Diện tích tam giác ABC là

$S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}40.60=1200c{m}^2$

Lại có: $S_{ABC}=\frac{1}{2}BE.AC=\frac{1}{2}BE.50=1200c{m}^2$

Tính toán tương tự $\Rightarrow CF=48cm$

Ví dụ 2: Cho tam giác ABC nhọn. Đường cao AD, BE, CF cắt nhau tại H.

Chứng minh $\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=1$ .

Lời giải:

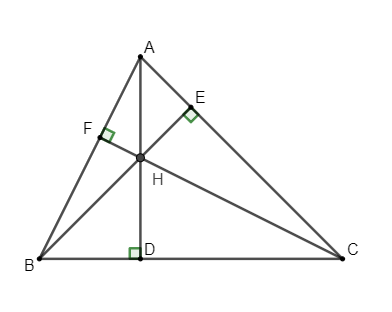
Diện tích tam giác ABC là

$S_{ABC}=\frac{1}{2}AD.BC=\frac{1}{2}BE.AC=\frac{1}{2}CF.AB$

Diện tích tam giác BHC là: $S_{BHC}=\frac{1}{2}HD.BC$

Diện tích tam giác AHC là: $S_{AHC}=\frac{1}{2}HE.AC$

Diện tích tam giác AHB là: $S_{AHB}=\frac{1}{2}HF.AB$

Tỉ số diện tích của tam giác BHC và tam giác ABC là:

$\frac{S_{BHC}}{S_{ABC}}=\frac{\frac{1}{2}HD.BC}{\frac{1}{2}AD.BC}=\frac{HD}{AD}$ (1)

Tỉ số diện tích của tam giác AHC và tam giác ABC là:

$\frac{S_{AHC}}{S_{ABC}}=\frac{\frac{1}{2}HE.AC}{\frac{1}{2}BE.AC}=\frac{HE}{BE}$ (2)

Tỉ số diện tích của tam giác AHB và tam giác ABC là:

$\frac{S_{AHB}}{S_{ABC}}=\frac{\frac{1}{2}HF.AB}{\frac{1}{2}CF.AB}=\frac{HF}{CF}$ (3)

Cộng vế với vế của (1); (2); (3) ta được:

$\frac{S_{BHC}}{S_{ABC}}+\frac{S_{AHC}}{S_{ABC}}+\frac{S_{AHB}}{S_{ABC}}=\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}$

$\iff \frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\frac{S_{BHC}+S_{AHC}+S_{AHB}}{S_{ABC}}$

$\iff \frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\frac{S_{ABC}}{S_{ABC}}=1$

Dạng 3: Tìm diện tích lớn nhất, nhỏ nhất của một hình

Phương pháp giải: Để tìm diện tích lớn nhất và nhỏ nhất của một hình ta có thể liên hệ giữa đường vuông góc và đường xiên.

Chú ý:

+ Nếu diện tích của một hình luôn lớn hơn hoặc bằng một số m và tồn tại vị trí của hình để diện tích bằng m thì m là diện tích nhỏ nhất của hình.

+ Nếu diện tích của một hình luôn nhỏ hơn hoặc bằng một số M và tồn tại vị trí của hình để diện tích bằng M thì M là diện tích lớn nhất của hình.

Ví dụ 1: Tìm diện tích lớn nhất của tam giác ABC biết AB = 3cm, BC = 4cm.

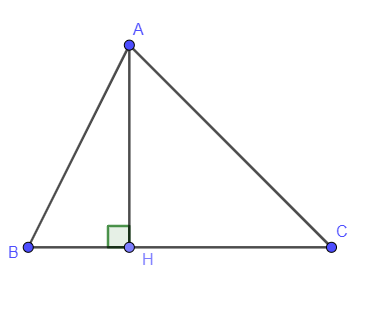
Vẽ AH vuông góc với BC tại H

Theo quan hệ đường vuông góc và đường xiên ta có:

$AH\le AB$

Khi đó diện tích tam giác ABC là

$S_{ABC}=\frac{1}{2}AH.BC\le \frac{1}{2}AB.BC$

$\Rightarrow S_{ABC}$ lớn nhất khi $S_{ABC}=\frac{1}{2}AB.BC$

Dấu “=” xảy ra khi AH$\equiv$ AB hay H$\equiv$B, tam giác ABC vuông tại B

Diện tích lớn nhất của tam giác ABC là:

$S_{ABC}=\frac{1}{2}AB.BC=\frac{1}{2}3.4=6c{m}^2$

Ví dụ 2: Tính diện tích lớn nhất của tam giác vuông ABC với cạnh huyền BC = a.

Lời giải:

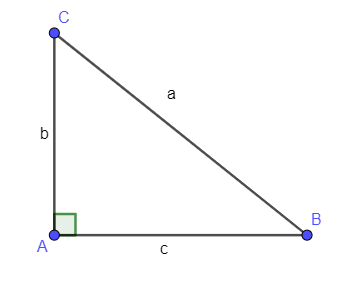
Đặt AC = b; AB = c

Xét tam giác ABC vuông tại A ta có:

$a^2=b^2+c^2$(định lý Py – ta – go)

Áp dụng bất đẳng thức cho hai số b, c ta có:

$bc\le \frac{b^2+c^2}{2}$

Diện tích tam giác ABC là:

$S_{ABC}=\frac{1}{2}bc\le \frac{1}{2}.\frac{b^2+c^2}{2}=\frac{b^2+c^2}{4}$

$S_{ABC}⩽\frac{b^2+c^2}{4}$

$\iff S_{ABC}\le \frac{a^2}{4}$

Dấu “=” xảy ra$\iff$ b = c

$\iff \Delta ABC$ vuông cân tại A

Vậy diện tích lớn nhất của tam giác ABC là $\frac{a^2}{4}$ khi tam giác ABC là tam giác vuông cân.

III. Bài tập tự luyện

Bài 1: Cho tam giác ABC, các đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm G . Chứng minh:

a) $S_{AGP}=S_{PGB}=S_{BGM}=S_{MGC}=S_{CGN}=S_{NGA}$ .

b) Các tam giác GAB; GBC và GCA có diện tích bằng nhau.

Bài 2: Cho tam giác ABC có cạnh BC = 60cm, đường cao AH; AH = 40cm. Gọi D và E theo thứ tự là trung điểm của AB và AC. Tính diện tích tứ giác BDEC.

Bài 3: Tính diện tích tam giác đều có cạnh bằng a.

Bài 4: Cho tam giác ABC. Hãy chỉ ra vị trí điểm M trong tam giác sao cho $S_{MAB}+S_{MAC}=S_{MBC}$ .

Bài 5: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh:

a)$S_{BMN}=\frac{1}{4}{S}_{ABC}$

b)$S_{MNPQ}=\frac{1}{2}{S}_{ABCD}$

Bài 6: Cho tam giác ABC có diện tích 30 $c{m}^2$ . G là trọng tâm tam giác. Tính diện tích tam giác BCG.

Bài 7: Cho tam gác ABC có AB = AC = 10cm, BC = 12cm. Tính độ dài đường cao BK.

Bài 8: Cho tam giác ABC, các đường trung tuyến BD và CE. Cho biết BC = 10cm, BD = 9cm, CE = 12cm.

a) Chứng minh BD vuông góc với CE

b) Tính diện tích tam giác ABC.

Bài 9: Cho tam giác ABC có BC = 6cm. Lấy M trên cạnh AC sao cho $AM=\frac{1}{3}AC$ . Xác định vị trí điểm N trên BC sao cho MN chia tam giác ABC thành hai phần thỏa mãn tứ giác AMNB có diện tích gấp ba lần diện tích MNC.

Bài 10: Các hình chữ nhật có độ dài đường chéo là 10cm. Hình nào có diện tích lớn nhất.

Xem thêm các dạng bài tập Toán lớp 8 có đáp án và lời giải chi tiết khác:

Diện tích hình thang và cách giải bài tập

Diện tích hình thoi và cách giải bài tập

Diện tích đa giác và cách giải bài tập

Đa giác, Đa giác lồi, Đa giác đều và cách giải bài tập

Diện tích hình chữ nhật và cách giải bài tập