Nội dung bài viết

    Xem thêm

    50 bài tập về cách chia đa thức một biến đã sắp xếp (có đáp án 2024) – Toán 8

    Với cách giải các dạng toán về cách chia đa thức một biến đã sắp xếp môn Toán lớp 8 Đại số gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về cách chia đa thức một biến đã sắp xếp lớp 8. Mời các bạn đón xem:

    1 35,071 29/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải - Toán lớp 8

    A. Lý thuyết:

    - Muốn chia đa thức một biến A cho đa thức một biến B≠0, trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên

    - Với A và B là hai đa thức tùy ý cùng một biến số (B≠0), khi đó tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R.

    Trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B.

    Nếu R = 0 thì phép chia A cho B là phép chia hết.

    R≠0 thì phép chia A cho B là phép chia có dư.

    Q được gọi là đa thức thương, R được gọi là dư trong phép chia A cho B.

    B. Các dạng bài:

    Dạng 1: Sử dụng hằng đẳng thức để thực hiện phép chia đa thức

    1. Phương pháp giải: Có thể dùng các hằng đẳng thức đấng nhớ sau để rút gọn phép chia đa thức:

    (A3+B3):(A+B)=A2−AB+B2(A3−B3):(A−B)=A2+AB+B2(A2−B2):(A+B)=A−B

    2. Ví dụ minh hoạ: Áp dụng hẳng đẳng thức đáng nhớ để thực hiện các phép chia sau:

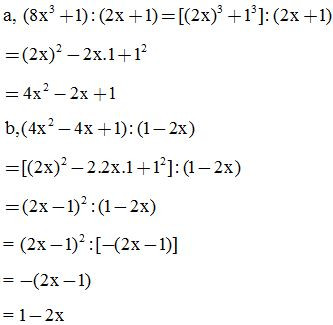
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Dạng 2: Tìm thương và số dư trong phép chia đa thức

    1. Phương pháp giải: Từ điều kiện đề bài đã cho, đặt phép chia A cho B rồi viết A dưới dạng A = B.Q + R

    2. Ví dụ minh họa:

    a, Cho hai đa thức A = x3-x2-5x-3 và B = x-3. Tìm dư R trong phép chia A cho B và viết A dưới dạng A = B.Q + R

    b, Cho đa thức A = 3x4+x3+6x−5 và B = x2+1. Tìm dư R trong phép chia A cho B và viết A dưới dạng A = B.Q + R

    Hướng dẫn giải:

    a, Ta thực hiện phép chia sau:

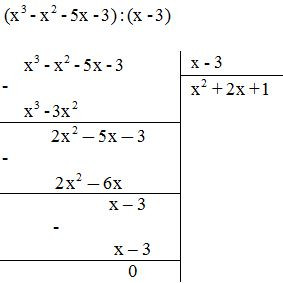
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    KL:

    - Vậy số dư trong phép chia là 0

    A = (x - 3).(x2+2x+1) + 0

    b, Ta thực hiện phép chia sau:

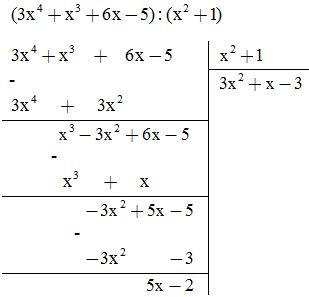
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    KL:

    - Vậy số dư trong phép chia là 5x – 2

    A = (x2+1).(3x2+x−3) + (5x – 2)

    Dạng 3: Tìm điều kiện để thực hiện phép chia đa thức

    1. Phương pháp giải:

    * Thực hiện phép chia A : B để tìm biểu thức dư R theo m

    Để A chia hết cho B thì R = 0⇒m

    * Tìm số nguyên n để A chia hết cho B (với A , B là các biểu thức theo n)

    - Thực hiện A : B tìm số dư là số nguyên k, thương là biểu thức Q

    - Viết A = Q.B + k

    - Để A chia hết cho B⇔k chia hết cho B⇔B là Ư(k)⇒n

    2. Ví dụ minh họa:

    VD1: Tìm k để f(x)=x4−9x3+21x2+x+k chia hết cho g(x) = x – 2

    Giải: Ta thực hiện phép chia sau:

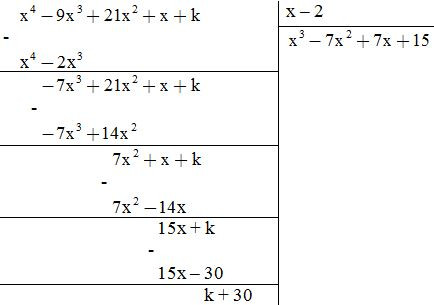
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Để f(x) chia hết cho g(x) thì k + 30 = 0⇔k = - 30.

    KL: Vậy với k = -30 thì f(x) chia hết cho g(x)

    VD2: Tìm số nguyên x để đa thức A = 8x2 - 4x +1 chia hết cho đa thức B = 2x + 1

    Giải: Ta thực hiện phép chia sau:

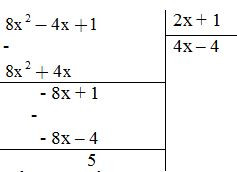
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Để A chia hết cho B thì 5 (2x + 1)⇔ (2x + 1)∈Ư(5)

    2x + 1

    5

    -5

    1

    -1

    x =

    2 (TM)

    -3 (TM)

    0 (TM)

    -1 (TM)

    KL: Vậy x = {-3, -1, 0, 2}

    3. Bài tập tự luyện

    Bài 1: Thực hiện phép chia sau:

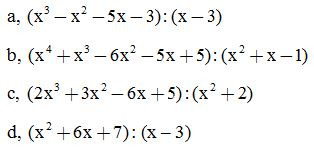
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Đs:

    a, Đây là phép chia hết với đa thức thương bằng x2+2x+1

    b, Đa thức thương bằng x2−5

    c, Đây là phép chia dư với đa thức thương bằng 2x + 3 và dư ( - 10x -1)

    d, Đây là phép chia dư với đa thức thương bằng x + 9 và dư 34

    Bài 2: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi tính:

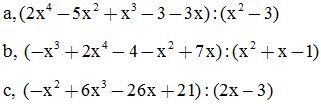
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Đs:

    a, Đây là phép chia hết với đa thức thương bằng 2x2+x+1

    b, Đây là phép chia hết với đa thức thương bằng 2x2−3x+4

    c, Đây là phép chia hết với đa thức thương bằng 3x2+4x−7

    Bài 3: Sử dụng hẳng đẳng thức để thực hiện các phép chia sau:

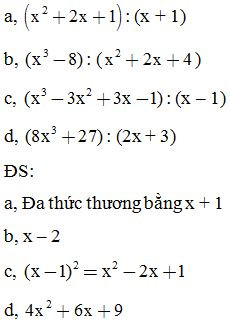
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Bài 4: Phân tích đa thức thành nhân tử rồi thực hiện phép chia:

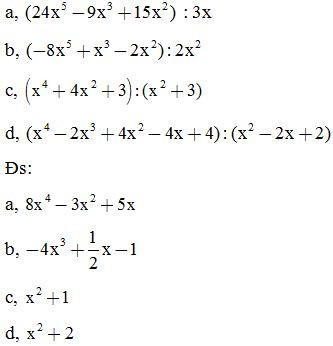
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Bài 5: Tìm thương Q và dư R sao cho A = B.Q + R, biết:

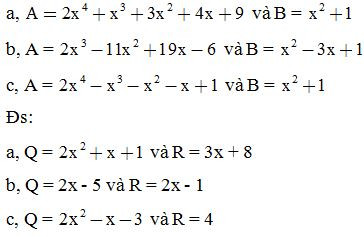
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Bài 6: Tìm k để:

    a, f(x) = x4 – 10x3 + 21x2 + 8x + k chia hết cho g(x) = x + 2

    b, f(x) = x4 – 19x3 + 25x2 - 6x + k chia hết cho g(x) = x – 3

    c, f(x) = x4 – 8x3 + 24x2 + 7x + k chia hết cho g(x) = x + 4

    d, f(x) = 3x4 – 7x3 + 11x2 + x + k chia hết cho g(x) = x – 4

    ĐS:

    a, k = - 164

    b, k = 225

    c, k = -1124

    d, k = 500

    Bài 7: Tìm a và b để đa thức A chia hết cho đa thức B, biết:

    a) A = x4 – 3x3 + 3x2 + ax + b và B = x2 - 3x + 4

    b) A = x4 – 9x3 + 21x2 + ax + b và B = x2 - x - 2

    ĐS:

    a, a = 3, b = -4

    b, a = 1, b = -30

    Bài 8: Tìm giá trị nguyên của x để đa thức A chia hết cho đa thức B, biết:

    a, A = 3x3 + 8x2 - 15x + 6 và B = 3x – 1

    b, A = x3 + 4x2 + ax - 7 và B = x + 4

    ĐS:

    a, x = 0, x = 1

    b, x = {-23, -5, -3, 15}

    Bài 9: Tìm đa thức M, biết:

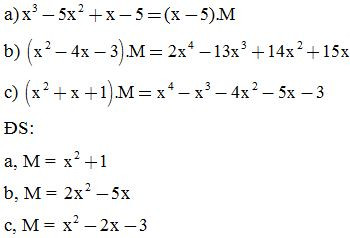
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Bài 10: Tìm x biết:

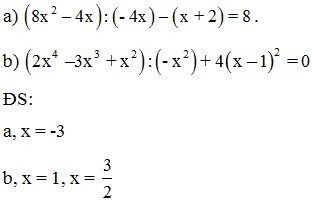
    Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải – Toán lớp 8 (ảnh 1)

    Xem thêm các dạng bài tập Toán lớp 8 có đáp án và lời giải chi tiết khác:

    Góc trong tứ giác và cách giải các dạng bài tập

    Hình thang, hình thang vuông, hình thang cân lớp 8 và cách giải

    Đối xứng trục, đối xứng tâm lớp 8 và cách giải bài tập

    Đường trung bình của tam giác, của hình thang và cách giải

    Các dạng toán về Hình bình hành và cách giải

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 35,071 29/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: