50 bài tập về hình thang, hình thang vuông, hình thang cân (có đáp án 2024) và cách giải

Hình thang, hình thang vuông, hình thang cân và cách giải

I. Lý thuyết về hình thang

1. Hình thang

- Tứ giác lồi có hai cạnh đối song song là hình thang.

- Hai cạnh song song đó gọi là hai cạnh đáy.

- Hai cạnh còn lại là hai cạnh bên.

Ta có: tứ giác ABCD có AB // CD nên ABCD là hình thang

Hai cạnh đáy là AB và CD

Hai cạnh bên là BC và AD

- Hai góc kề một cạnh bên của hình thang có tổng bằng $180°$

$\widehat{A}+\widehat{D}=180°;\widehat{B}+\widehat{C}=180°$

2. Hình thang cân

- Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

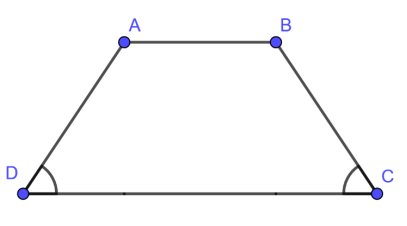
- Tính chất của hình thang cân:

Hình thang ABCD cân có AB // CD

+ Hai góc kề một đáy bằng nhau ($\widehat{A}=\widehat{B}$ ; $\widehat{C}=\widehat{D}$)

+ Hai cạnh bên bằng nhau (BC = AD)

+ Hai đường chéo bằng nhau (AC = BD)

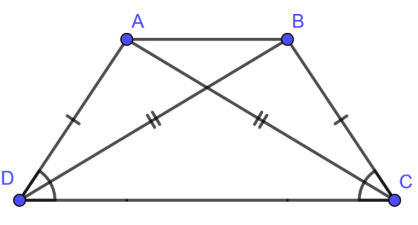
Dấu hiệu nhận biết:

+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

+ Hình thang có hai đường chéo bằng nhau là hình thang cân.

Chú ý: Hình thang có hai cạnh bên bằng nhau chưa chắc đã là hình thang cân.

3. Hình thang vuông

Hình thang vuông là hình thang có một góc vuông.

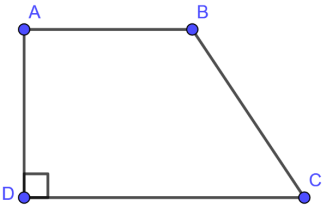
Cho hình thang ABCD có $\widehat{D}=90°$ nên hình thang ABCD là hình thang vuông

II. Công thức tính chu vi, diện tích hình thang

- Công thức tính chu vi hình thang: bằng tổng độ dài của 2 đáy và 2 cạnh bên

P = a + b + c + d

- Công thức tính diện tích hình thang: bằng trung bình cộng 2 đáy nhân với chiều cao

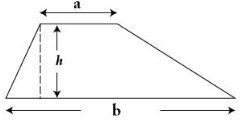
S = $\frac{a + b}{2}$.h

Muốn tính diện tích hình thang

Đáy lớn đáy nhỏ ta đem cộng vào

Cộng vào nhân với chiều cao

Chia đôi lấy nửa thế nào cũng ra

* Cách tính diện tích hình thang cân

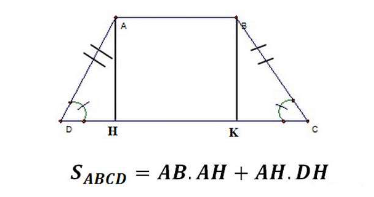
III. Các dạng bài tập và phương pháp giải

Dạng 1. Tính số đo góc

Phương pháp giải: Sử dụng tính chất hai đường thẳng song song và tổng bốn góc trong một tứ giác kết hợp với kiến thức đã học về hình thang, hình thang cân, hình thang vuông.

Ví dụ 1: Cho hình thang ABCD có AB // CD, $\widehat{A}=3\widehat{D}$, $\widehat{B}-\widehat{C}=30°$. Tính số đo các góc của hình thang.

Lời giải:

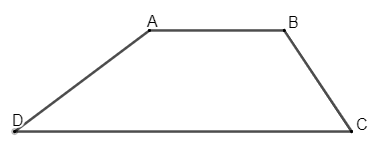
Vì AB // CD nên ta có

$\widehat{A}+\widehat{D}=180°$(hai góc trong cùng phía)

Mà $\widehat{A}=3\widehat{D}$

Nên $3\widehat{D}+\widehat{D}=180°$

$\begin{array}{l}\Rightarrow 4\widehat{D}=180°\\ \Rightarrow \widehat{D}=45°\\ \Rightarrow \widehat{A}=3\widehat{D}=45°.3=135°\end{array}$

Vì AB // CD nên ta có:

$\widehat{B}+\widehat{C}=180°$ (*)

Mà $\widehat{B}-\widehat{C}=30°$

$\Rightarrow \widehat{B}=30°+\widehat{C}$

Thay vào (*) ta được:

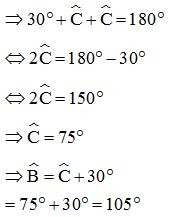
Ví dụ 2: Cho hình thang cân ABCD có AB // CD. Biết $\widehat{A}=2\widehat{D}$. Tính các góc của hình thang.

Lời giải

Vì AB // CD ta có:

$\widehat{A}+\widehat{D}=180°$ (hai góc trong cùng phía)

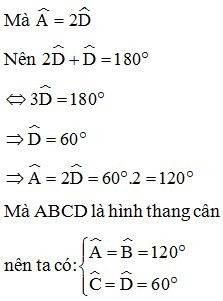
Dạng 2. Chứng minh hình thang, hình thang cân hình thang vuông

Phương pháp giải: Sử dụng định nghĩa hình thang, hình thang cân, hình thang vuông.

Ví dụ 1: Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến của tam giác. Chứng minh BCDE là hình thang cân.

Lời giải:

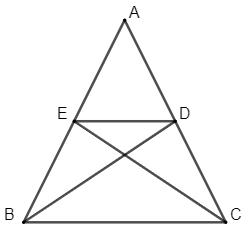
Vì BD là đường trung tuyến của tam giác ABC nên D là trung điểm của AC.

$\Rightarrow AD=\frac{1}{2}AC$

Vì CE là đườg trung tuyến của tam giác ABC nên E là trung điểm của AB

$\Rightarrow AE=\frac{1}{2}AB$

Mà AB = AC (do tam gác ABC cân tại A)

Do đó: AD = AE

Xét tam giác AED có

AD = AE ( chứng minh trên)

Do đó: $\Delta AED$ cân tại A

Ta có:

$\widehat{A}+\widehat{AED}+\widehat{ADE}=180°$ (tổng ba góc trong một tam giác)

$\widehat{A}+2\widehat{AED}=180°$ (do tam giác AED cân tại A nên $\widehat{AED}=\widehat{ADE}$)

$2\widehat{AED}=180°-\widehat{A}$

$\widehat{AED}=\frac{180°-\widehat{A}}{2}$(1)

Lại có: $\Delta ABC$ cân tại A nên:

$\widehat{A}+\widehat{ABC}+\widehat{ACB}=180°$(tổng ba góc trong một tam giác)

Suy ra: $\widehat{A}+2\widehat{ABC}=180°$

$2\widehat{ABC}=180°-\widehat{A}$

$\widehat{B}=\frac{180°-\widehat{A}}{2}$(2)

Từ (1) và (2)$\Rightarrow \widehat{ABC}=\widehat{AED}$

Mà hai góc này ở vị trí đồng vị nên ED //BC

$\Rightarrow$Tứ giác BCDE là hình thang

Mặt khác: $\Delta ABC$ cân tại A nên $\widehat{ABC}=\widehat{ACB}$ hay $\widehat{EBC}=\widehat{DCB}$

Vậy hình thang BCDE là hình thang cân (do có hai góc kề một đáy bằng nhau).

Ví dụ 2: Cho tam giác ABC vuông cân tại A. Vẽ về phía ngoài tam giác ACD vuông cân tại D. Tứ giác ABCD là hình gì? Vì sao?

Lời giải:

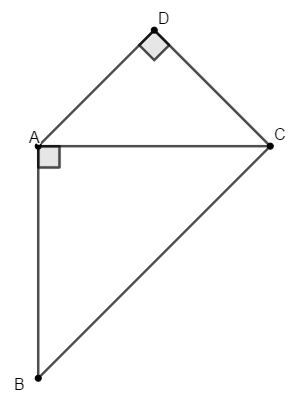
Dạng 3. Sử dụng các tính chất của hình thang, hình thang cân, hình thang vuông để chứng minh bài toán

Phương pháp giải: Áp dụng các tính chất về cạnh và góc của hình thang, hình thang cân, hình thang vuông đã học để giải quyết bài toán.

Ví dụ 1: Cho hình thang vuông ABCD có $\widehat{A}=\widehat{D}=90°$, AB = AD , DC = 2AB và BE vuông góc với CD tại E.

a) Chứng minh: $\Delta ABD=\Delta EDB$

b) Chứng minh: $∆BEC$ vuông cân tại E.

Lời giải:

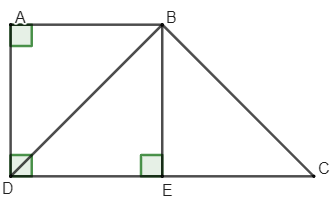
a) Do ABCD là hình thang nên AB // CD

$\Rightarrow \widehat{ABD}=\widehat{BDC}$ (hai góc so le trong)

Vì BE vuông góc với DC$\Rightarrow \widehat{BED}=90°$

Xét và tam giác $\Delta EDB$ ta có:

BD chung

$\widehat{A}=\widehat{BED}=90°$

$\widehat{ABD}=\widehat{BDC}$

Do đó: $\Delta ABD=\Delta EDB$(cạnh huyền - góc nhọn)

b) Từ hai tam giác bằng nhau ở câu a ta có:

AB = ED, AD = EB (các cặp cạnh tương ứng)

Mà $\text{AB=}\frac{1}{2}CD$$\Rightarrow ED=\frac{1}{2}CD$

Suy ra E là trung điểm của CD

$\Rightarrow$ED = AB = EC

Mà AB = AD (giả thuyết)

Nên ED = AB = EC = AD = EB

Xét tam giác BEC có

EB = EC

$\widehat{BEC}=90°$

Vậy $\Delta BEC$ là tam giác vuông cân tại E

Ví dụ 2: Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi G là giao điểm của AD và BC. Gọi F là giao điểm của AC và BD. Chứng minh:

a) Tam giác AGB cân tại G;

b) Các tam giác ABD và BAC bằng nhau;

c) FC = FD.

Lời giải:

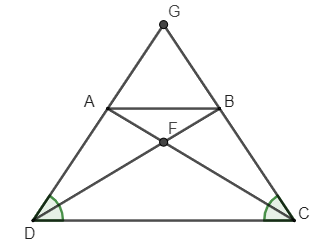
a) Vì AB // CD nên ta có:

$\widehat{GAB}=\widehat{ADC}$(hai góc đồng vị)

$\widehat{GBA}=\widehat{BCD}$(hai góc đồng vị)

Mà $\widehat{ADC}=\widehat{BCD}$ (do ABCD là hình thang cân)

Do đó: $\widehat{GAB}=\widehat{GBA}$

Xét tam giác AGB có:

$\widehat{GAB}=\widehat{GBA}$

Nên tam giác AGB là tam giác cân tại G.

b) Xét hai tam giác ABD và BAC có:

AB chung

AD = BC (do ABCD là hình thang cân)

AC = BD (do ABCD là hình thang cân)

Do đó: $\Delta ABD=\Delta BAC$ (c – c – c)

c) Ta có:

$\left\{\begin{array}{l}\widehat{ADC}=\widehat{ADB}+\widehat{BDC}\\ \widehat{BCD}=\widehat{BCA}+\widehat{ACD}\end{array}\right.$

$\iff \left\{\begin{array}{l}\widehat{ADC}-\widehat{ADB}=\widehat{BDC}\\ \widehat{BCD}-\widehat{BCA}=\widehat{ACD}\end{array}\right.$

Mà $\widehat{ADB}=\widehat{BCA}$ (do $\Delta ABD=\Delta BAC$); $\widehat{ADC}=\widehat{BCD}$ (ABCD là hình thang cân)

Do đó: $\widehat{BDC}=\widehat{ACD}$

Xét tam giác FCD có:

$\widehat{FDC}=\widehat{FCD}$ $(\widehat{BDC}=\widehat{ACD})$

Suy ra tam giác FCD cân tại F

$\Rightarrow$FC = FD (điều phải chứng minh)

IV. Bài tập tự luyện

Bài 1: Cho hình thang ABCD có AB // CD, $\widehat{A}=3\widehat{D}$. Tính các góc của hình thang.

Bài 2: Cho hình thang ABCD (AB // CD), có AH và BK là hai đường cao của hình thang.

a) Chứng minh: $DH=\frac{CD-AB}{2}$

b) Biết AB = 6cm, CD = 14cm, AD = 5cm. Tính DH, AH và diện tích hình thang ABCD.

Bài 3: Cho hình thang ABCD (AB // CD) có CD = AD + BC. Gọi K là điểm thuộc đáy CD sao cho KD = AD. Chứng minh:

a) AK là tia phân giác góc A.

b) KC = BC.

Bài 4: Cho tam giác ABC vuông cân tại A có AB = 4cm. Vẽ về phía ngoài tam giác ACD vuông cân tại D. Tính diện tích tứ giác ABCD.

Bài 5: Cho hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của góc $\widehat{BCD}$

Bài 6: Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm hai đáy AB và CD. Chứng minh EF vuông góc với AB.

Bài 7: Cho hình thang ABCD vuông tại A và D. Có AB = AD = 3cm, CD = 6cm. Tính số đo góc B, góc C.

Bài 8: Cho hình thang ABCD (AB // CD), Hai đường phân giác của góc C và góc D cắt nhau tại I thuộc đáy AB. Chứng minh rằng tổng độ dài hai cạnh bên bằng độ dài AB của hình thang.

Bài 9: Cho hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng AC là tia phân giác của góc C.

Bài 10: Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho CM = CA. Đường thẳng qua M song song với CA cắt AB tại I.

a) Tứ giác ACMI là hình gì?

b) AB + AC < AH + BC.

Xem thêm các dạng bài tập Toán lớp 8 có đáp án và lời giải chi tiết khác:

Đối xứng trục, đối xứng tâm lớp 8 và cách giải bài tập

Đường trung bình của tam giác, của hình thang và cách giải

Các dạng toán về Hình bình hành và cách giải

Các dạng toán về Hình chữ nhật và cách giải

50 bài tập về hình thoi (có đáp án 2022) – Toán 8