Nội dung bài viết

    Xem thêm

    50 bài tập về công thức diện tích hình bình hành (có đáp án 2024) – Toán 8

    Với Công thức diện tích hình bình hành hay, chi tiết Toán lớp 8 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các công thức về Công thức diện tích hình bình hành từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

    1 589 29/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức diện tích hình bình hành hay, chi tiết - Toán lớp 8

    I. Lí thuyết

    Diện tích hình bình hành bằng tích của một cạnh nhân với chiều cao ứng với cạnh đó

    S = a.h với a là độ dài cạnh đáy, h là độ dài chiều cao tương ứng.

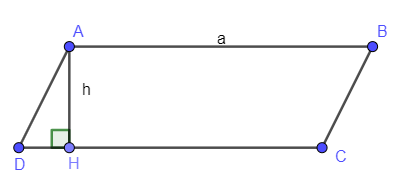
    Tài liệu VietJack

    Cho hình bình hành ABCD có CD = AB = a, đường cao AH = h. Diện tích hình bình hành là:

    SABCD=CD.AH=a.h (đơn vị diện tích)

    II. Các ví dụ

    Ví dụ 1: Tính số đo góc D^ của hình bình hành ABCD có diện tích là 30cm2 , AB = 10cm, AD = 6cm,A^>D^ .

    Lời giải:

    Tài liệu VietJack

    Kẻ AH là đường cao của hình bình hành, AH vuông góc với CD tại H.

    Vì ABCD là hình bình hành nên AB = CD = 10cm; BC = AD = 6cm.

    Ta có:

    SABCD=AH.CD

    ⇔30=AH.10

    ⇔AH=3cm (1)

    Gọi E là trung điểm của AD nên EA = ED = 3cm (2)

    Xét tam giác AHD vuông tại H, có E là trung điểm của AD nên HE là đường trung tuyến ứng với cạnh huyền.

    ⇒HE=12AD=12.6=3cm (3)

    Từ (1); (2); (3)⇒HE=AH=AE=3cm

    ⇒Tam giác AHE là tam giác đều

    ⇒EAH^=60°⇒DAH^=60°

    Xét tam giác AHD có:

    DAH^+DHA^+ADH^=180°(định lý tổng ba góc trong một tam giác).

    ⇔60°+90°+ADH^=180°

    ⇒ADH^=180°−90°−60°

    ⇔ADH^=30°

    Vậy D^=30°.

    Ví dụ 2: Cho hình bình hành ABCD, M là trung điểm của AD, qua M kẻ đường thẳng d cắt AB, CD lần lượt tại E và F. Kẻ MH vuông góc với BC tại H.

    Chứng minh: SEBCF=MH.BC .

    Lời giải:

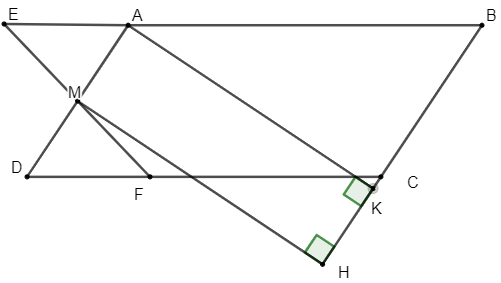
    Tài liệu VietJack

    Vì ABCD là hình bình hành nên AB // CD mà E thuộc AB, F thuộc CD nên AE // DF

    ⇒EAM^=MDF^ (hai góc so le trong)

    Vì M là trung điểm của AD nên AM = MD
    Xét tam giác AEM và tam giác DFM có:

    EAM^=MDF^(chứng minh trên)

    AM = DM (chứng minh trên)

    EMA^=FMD^(hai góc đối đỉnh)

    Do đó:ΔAEM=ΔDFM (g – c - g)

    ⇒SAEM=SDFM (1)

    Ta có:

    SEBCF=SAEM+SMABCF (2)

    SABCD=SDFM+SMABCF (3)

    Từ (1); (2); (3) ⇒SEBCF=SABCD (4)

    Kẻ AK vuông góc với BC tại K

    Vì AK vuông góc với BC nên AK là đường cao của hình bình hành ABCD.

    Lại có AK vuông góc với BC; MH vuông góc với BC nên MH // AK

    Xét tứ giác AKHM có:

    AK // MH (chứng minh trên)

    AM //HK (do ABCD là hình bình hành)

    Do đó tứ giác AKHM là hình bình hành

    ⇒AK=MH

    Ta có:

    SABCD=AK.BC(mà AK = MH)

    ⇒SABCD=MH.BC (5)

    Từ (4) và (5)⇒SEBCF=MH.BC (điều phải chứng minh).

    Xem thêm tổng hợp công thức môn Toán lớp 8 đầy đủ và chi tiết khác:

    Công thức diện tích hình thoi hay, chi tiết

    Công thức diện tích tứ giác có hai đường chéo vuông góc hay, chi tiết

    Công thức tính diện tích đa giác hay, chi tiết

    Công thức diện tích hình chữ nhật hay, chi tiết

    Công thức diện tích hình vuông hay, chi tiết

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 589 29/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: