Các phương pháp phân tích đa thức thành nhân tử, bài tập và cách giải (2024) – Toán 8

Các phương pháp phân tích đa thức thành nhân tử chi tiết nhất - Toán lớp 8

A. Phương pháp đặt nhân tử chung

I. Lý thuyết

- Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

- Phương pháp đặt nhân tử chung là một phương pháp để phân tích đa thức thành nhân tử bằng cách nhóm các hạng tử có chung nhân tử:

A.B + A.C = A.(B + C)

II. Các dạng bài

1. Dạng 1: Phân tích đa thức thành nhân tử:

a. Phương pháp giải:

Phân tích các hạng tử của đa thức để chọn nhân tử chung thích hợp, sau đó áp dụng tính chất phân phối của phép nhân với phép cộng

b, Ví dụ minh họa:

Phân tích các đa thức sau thành nhân tử:

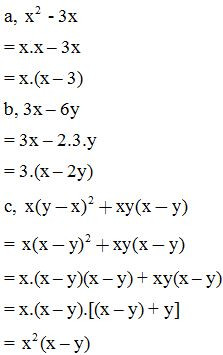
2. Dạng 2: Các bài toán liên quan

a. Phương pháp giải:

Phân tích các hạng tử của đa thức để chọn nhân tử chung thích hợp, sau đó áp dụng tính chất phân phối của phép nhân với phép cộng để làm một số bài toán tính nhanh, tính giá trị biểu thức, tìm x,…

b. Ví dụ minh họa

VD1: Tính nhanh:

a, 75.20,9 + 5² .20,9

= 20,9.(75 + 5²)

= 20,9.100

= 2090

b, 98,6.199 – 990.9,86

= 98,6.199 – 99.10.9,86

= 98,6.199 – 98,6.99

= 98,6.(199 – 99)

= 98,6.100

= 9860

VD2: Tính giá trị biểu thức:

a, A = a(b + 3) – b(3 + b) tại a = 2, b = 3

A = a(b + 3) – b(b + 3)

= (b + 3)(a – b)

Thay a = 2, b = 3 vào biểu thức A ta được:

A = (3 + 3)(2 – 3) = - 6

b, B = b² - 8b – c(8 – b) tại b = 1, c = 2

Ta có:

B = b² - 8b – c(8 – b)

= -b(8 – b) – c(8 – b)

= (8 – b)(- b – c)

Thay b = 1, c = 2 vào biểu thức B, ta được:

B = (8 – 1)(- 1 – 2)

= -21

VD3: Tìm x, biết:

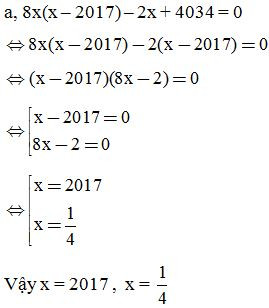
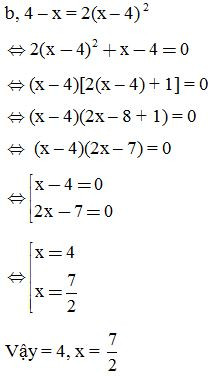
3. Dạng 3: Chứng minh các bài toán số nguyên:

a. Phương pháp giải:

Phân tích các biểu thức đã cho một cách hợp lí thành các tích và sử dụng tính chất chia hết của số nguyên.

b. Ví dụ minh họa:

Chứng minh:

a, 25ⁿ⁺¹-25ⁿ chia hết cho 100 với mọi số tự nhiên n$\ne 0$

Ta có:

25ⁿ⁺¹ - 25ⁿ

= 25ⁿ (25 – 1)

= 24.25ⁿ

Ta lại có: 24 = 4.6

25ⁿ = 25.25^n-1

$\Rightarrow$25ⁿ⁺¹ - 25ⁿ = 4.6.25.25^n-1

= 100.6.25$⋮$100 với mọi $n\in {\mathbb{N}}^{*}$

Vậy 25ⁿ⁺¹ - 25ⁿ chia hết cho 100 với mọi số tự nhiên n

b, n²(n - 1) - 2n(n - 1) chia hết cho 6 với mọi số nguyên n

Ta có:

n²(n - 1) - 2n(n - 1)

= (n – 1)(n² - 2n)

= (n – 1).n.(n – 2)

= (n – 2).(n – 1).n

Ta có: n – 2, n – 1, n là 3 số tự nhiên liên tiếp nên tích của chúng sẽ chia hết 6

$\Rightarrow$n²(n - 1) - 2n(n - 1) chia hết cho 6 với mọi số nguyên n.

c, 50ⁿ⁺² - 50ⁿ⁺¹ chia hết cho 245 với mọi số tự nhiên n.

Ta có:

50ⁿ⁺² - 50ⁿ⁺¹

= 50ⁿ (50² - 50)

= 50ⁿ (2500 – 50)

= 2450.50ⁿ

= 245.10.50ⁿ $⋮$245 với mọi STN n

Vậy 50ⁿ⁺² - 50ⁿ⁺¹ chia hết cho 245 với mọi số tự nhiên n.

B. Phương pháp dùng hằng đẳng thức

I. Lý thuyết:

- Ta có thể sử dụng các hằng đẳng thức đáng nhớ theo chiều biến đổi từ một vế là một đa thức sang vế kia là một tích của các nhân tử hoặc lũy thừa của một đơn thức đơn giản hơn.

II. Các dạng bài:

1. Dạng 1: Phân tích đa thức thành nhân tử

a. Phương pháp giải:

Chuyển các đa thức đã cho về đúng dạng của hẳng đẳng thức cần sử dụng và phân tích thành nhân tử.

b. Ví dụ minh họa:

Phân tích đa thức thành nhân tử:

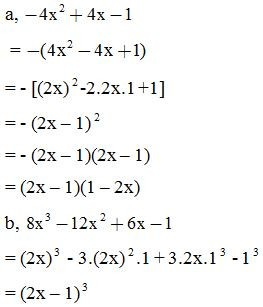
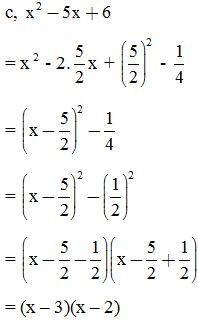
2. Dạng 2: Các bài toán liên quan

a. Phương pháp giải

Sử dụng hằng đẳng thức một cách hợp lý để phân tích các biểu thức để làm một số bài toán tính nhanh, tìm x,…

b. Ví dụ minh họa:

VD1: Tính nhanh:

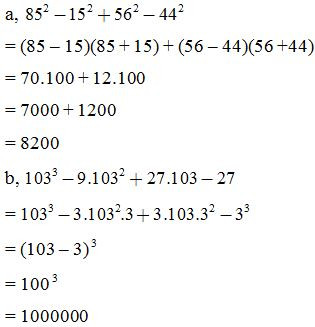
VD2: Tìm x:

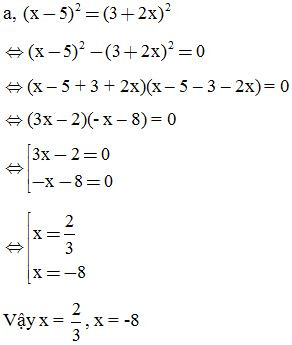
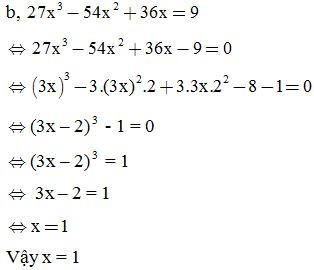
3. Dạng 3: Chứng minh các bài toán số học:

a. Phương pháp giải:

Số nguyên a chia hết cho số nguyên b nếu có số nguyên k sao cho a = b.k. Từ đó cần phân tích biểu thức ra thừa số để xuất hiện số chia.

b. Ví dụ minh họa:

Chứng minh:

a, (3n -1)² - 4 chia hết cho 3 với mọi số tự nhiên n

Ta có:

(3n -1)² - 4 = (3n -1)² - 2²

= (3n – 1 – 2)(3n – 1 + 2)

= (3n – 3)(3n + 1)

= 3.(n – 1)(3n +1)$⋮$3 với mọi STN n

b, 100 - (7n +3)² chia hết cho 7 với mọi STN n

Ta có:

100 - (7n +3)² = 10² - (7n +3)²

= (10 – 7n - 3)(10 + 7n + 3)

= (7 – 7n)(13 + 7n)

= 7.(1 – n)(13 + 7n)$⋮$7 với mọi STN n

C. Phương pháp nhóm hạng tử

I. Lý thuyết

- Khi sử dụng phương pháp nhóm hạng tử để phân tích đa thức thành nhân tử, ta cần nhận xét đặc điểm của các hạng tử, nhóm các hạng tử một cách thích hợp nhằm làm xuất hiện dạng hằng đẳng thức hoặc xuất hiện nhân tử chung của các nhóm.

II. Các dạng bài

1. Dạng 1: Phân tích đa thức thành nhân tử

a. Phương pháp giải:

Nhóm các hạng tử một cách hợp lí để xuất hiện nhân tử chung hoặc xuất hiện các hằng đẳng thức

b. Ví dụ minh họa:

Phân tích các đa thức sau thành nhân tử:

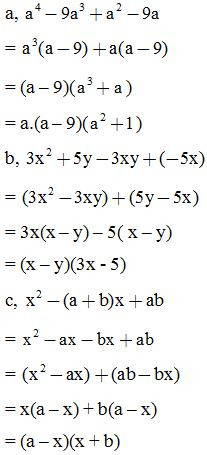
2. Dạng 2: Các bài toán liên quan

a. Phương pháp giải:

Nhóm các hạng tử một cách hợp lí để xuất hiện nhân tử chung hoặc xuất hiện các hằng đẳng thức sau đó áp dụng để tính nhanh, tính giá trị biểu thức hoặc tìm x,….

b. Ví dụ minh họa:

VD1: Tính nhanh:

VD2: Tìm x:

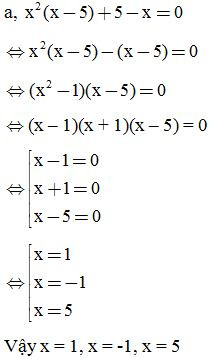
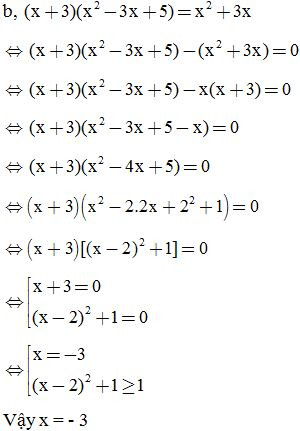
3. Dạng 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức dạng ax² + bx + c

a. Phương pháp giải:

Tách hạng tử c thành tổng $c_1+c_2$ sao cho $a{x}^2+bx+c_1$ tạo thành bình phương của một tổng hoặc bình phương của một hiệu rồi đánh giá.

b. Ví dụ minh họa:

VD1: Tìm GTNN của biểu thức:

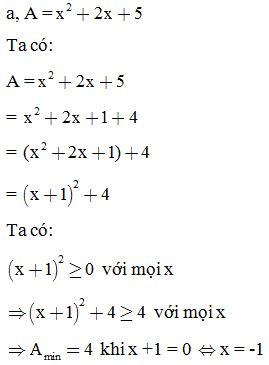
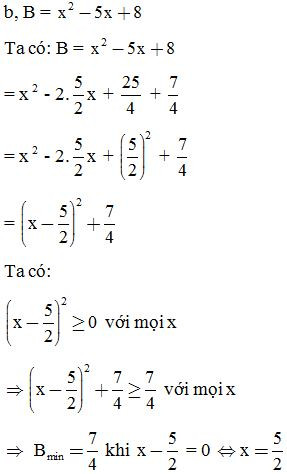
D. Phối hợp nhiều phương pháp

I. Lý thuyết

- Một số phương pháp phân tích đa thức thành nhân tử cơ bản đã học trong các bài trước:

+ Phương pháp nhân tử chung

+ Phương pháp hằng đẳng thức

+ Phương pháp nhóm hạng tử

- Trong một số bài toán thì chúng ta cần kết hợp linh hoạt cả ba phương pháp cơ bản trên để phân tích đa thức thành nhân tử

- Ngoài ra, để phân tích đa thức thành nhân tử người ta còn sử dụng một số phương pháp khác như:

+ Phương pháp tách hạng tử

+ Phương pháp thêm, bớt cùng một hạng tử

+ Phương pháp đặt biến phụ

+ Phương pháp hệ số bất định.

…

II. Các dạng bài

1. Dạng 1: Phân tích đa thức thành nhân tử bằng cách phối hợp các phương pháp cơ bản

a. Phương pháp giải:

Sử dụng phối hợp nhiều phương pháp cơ bản để phân tích đa thức thành nhân tử:

+ Phương pháp nhân tử chung

+ Phương pháp hằng đẳng thức

+ Phương pháp nhóm hạng tử

b. Ví dụ minh họa:

Phân tích các đa thức sau thành nhân tử:

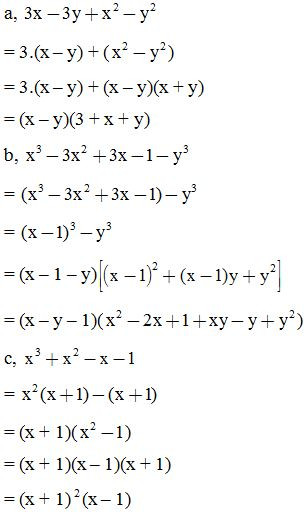
2. Dạng 2: Phân tích đa thức thành nhân tử bằng phương pháp tách hạng tử

a. Phương pháp giải:

Tách một hạng tử thành nhiều hạng tử sau đó sử dụng phương pháp nhóm hạng tử để phân tích.

Chú ý: Đối với các đa thức có dạng $a{x}^2+bx+c (a\ne 0)$ ta thường sử dụng cách tách sau để phân tích đa thức thành nhân tử:

+ Cách 1: Tách $bx=b_{1}x+b_{2}x$ sao cho $b_1{b}_2=ac$

+ Cách 2: Tách c =$c_1+c_2$ sao cho $a{x}^2+bx+c_1=$${(\mathrm{...}\pm \mathrm{...})}^2$

b. Ví dụ minh họa:

Phân tích các đa thức sau thành nhân tử:

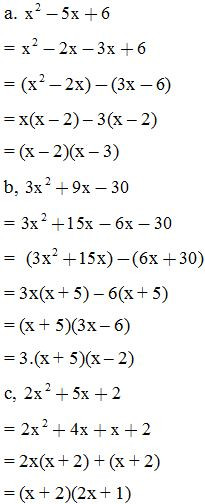
3. Dạng 3: Phân tích đa thức thành nhân tử bằng phương pháp đặt biến phụ

a. Phương pháp giải:

Đặt các hạng tử giống nhau thành biến mới để đưa các đa thức đã cho ở đề bài về một đa thức mới với biến vừa đặt sau đó sử dụng các phương pháp phân tích đã học ở trên để phân tích đa thức thành nhân tử.

b. Ví dụ minh họa:

Phân tích các đa thức sau thành nhân tử:

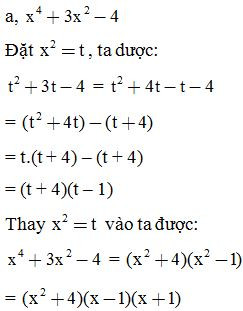
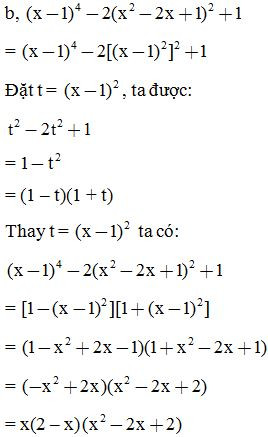
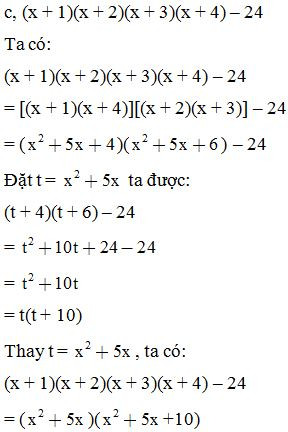
E. Phương pháp tách

Ta có thể tách 1 hạng tử nào đó của đa thức thành hai hay nhiều hạng tử thích hợp để làm xuất hiện những nhóm hạng tử mà ta có thể dùng các phương pháp khác để phân tích được

Ví dụ: Phân tích đa thức sau thành nhân tử bằng phương pháp tách hạng tử.

A = x² + 7x + 6 = x² + x + 6x + 6 = x(x + 1) + 6(x + 1) = (x + 6)(x + 1)

F. Phương pháp thêm bớt cùng một hạng tử

Ta có thể thêm bớt 1 hạng tử nào đó của đa thức để làm xuất hiện những nhóm hạng tử mà ta có thể dùng các phương pháp khác để phân tích được.

Ví dụ

A = x³ + x² - 3x + 1

= (x³ - x²) + x² + x² - 3x + 1

= x² (x - 1) + 2x (x -1) - (x - 1)

= (x - 1) (x² + 2x - 1)

G. Phương pháp đặt biến phụ

Trong một số trường hợp, để việc phân tích đa thức thành nhân tử được thuận lợi, ta phải đặt biến phụ thích hợp.

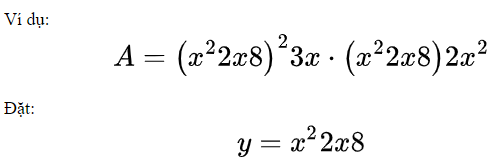
Ta có:

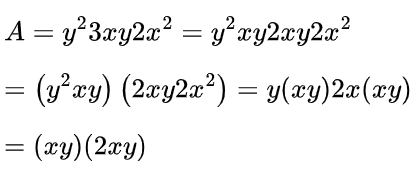
H. Phương pháp giảm dần số mũ của lũy thừa

Phương pháp này chỉ áp dụng được cho các đa thức như

là những đa thức có dạng

.

Khi phân tích các đa thức có dạng như trên thì biểu thức sau khi phân tích đều có 1 nhân tử là

a² + a + 1

Ví dụ: Phân tích đa thức thành nhân tử

A = a⁵ + a⁴+1

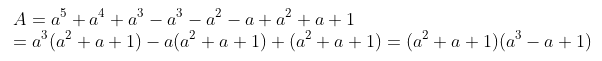
I. Phương pháp hệ số bất định

Hệ số bất định là gì? Hệ số thì chúng ta biết rồi, trong biểu thức chúng ta có các phần là [phần hệ số][phần biến]. Ví dụ như 5x thì hệ số là 5 và biến số là x. Bất định là gì, bất định là chưa xác định được. Vậy Hệ số bất định hiểu nôm na là phần hệ số chưa xác định. Vậy làm sao để chúng ta có thể xác định được phần hệ số này, thì dạng toán hệ số bất định này luôn đi kèm với dạng toán “Đồng nhất đathức”. Có thể hiểu như sau, đa thức A bằng đa thức B khi các hệ số cùng bậc của đa thức A bằng các hệ số cùng bậc của đa thức B.

Ví dụ sau khi phân tích 1 bài tìm a,b chúng ta được: 5x + 6y = (1-a)x + (b+2)y
Thì (1-a) và (b+2) ở đây đóng vai trò như các hệ số bất định. Chúng ta đi đồng nhất đa thức thì:

5x = (1-a)x và 6y = (b+2)y Hay 5 = 1- a và 6 = b+2.

K. Bài tập tự luyện

Bài 1: Phân tích các đa thức sau thành nhân tử

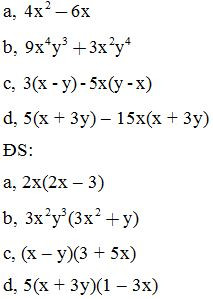
Bài 2: Phân tích đa thức thành nhân tử

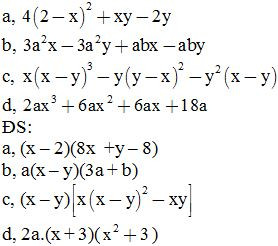
Bài 3: Tính hợp lí

Bài 4: Tính giá trị biểu thức

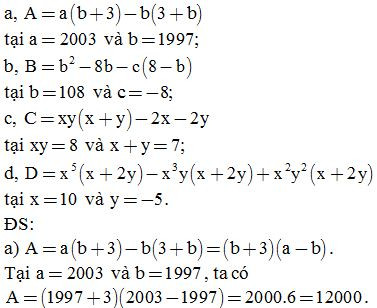
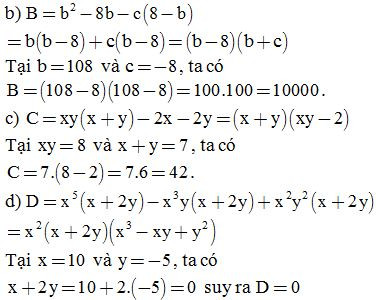
Bài 5: Tìm x, biết

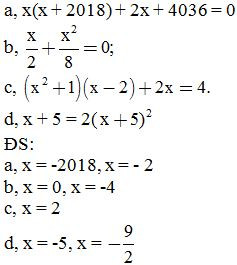
Bài 6:

a) ${15}^n+{15}^{n+2}$ chia hết cho 113 với mọi số tự nhiên

b) $n^4-n^2$ chia hết cho 4 với mọi số tự nhiên

ĐS:

Bài 7: Phân tích các đa thức sau thành nhân tử:

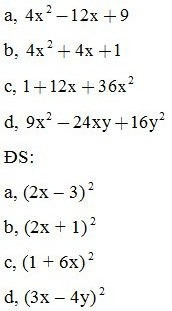
Bài 8: Phân tích các đa thức sau thành nhân tử:

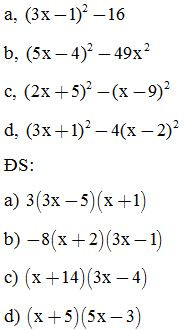
Bài 9: Phân tích các đa thức sau thành nhân tử:

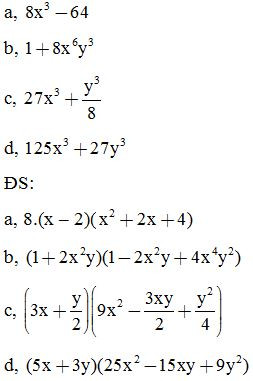
Bài 10: Phân tích các đa thức sau thành nhân tử:

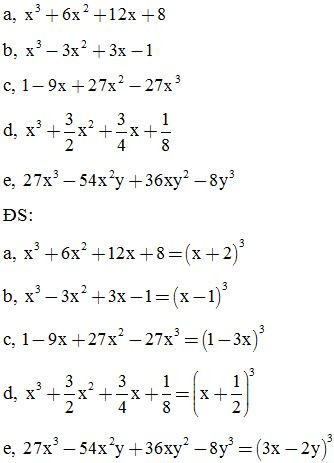
Bài 11: Phân tích các đa thức sau thành nhân tử:

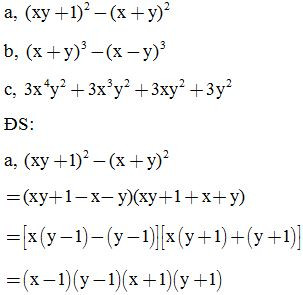
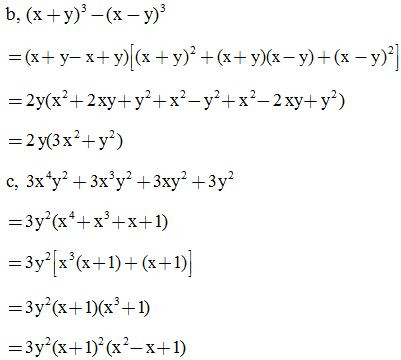
Bài 12: Phân tích các đa thức sau thành nhân tử

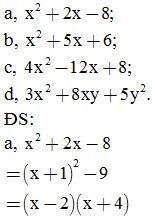
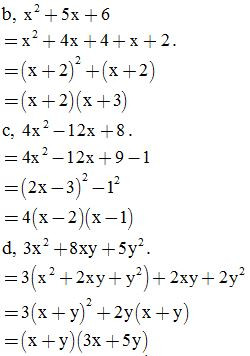
Bài 13: Tìm x, biết

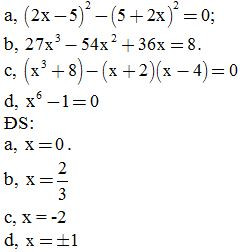
Bài 14: Chứng minh

a, $2^9-1$ chia hết cho 73

b, $5^6-{10}^4$ chia hết cho 9

c, ${\left(n+3\right)}^2-{\left(n-1\right)}^2$ chia hết cho 8 với mọi số tự nhiên n

d, ${\left(n+6\right)}^2-{\left(n-6\right)}^2$ chia hết cho 24 với mọi số tự nhiên n

ĐS:

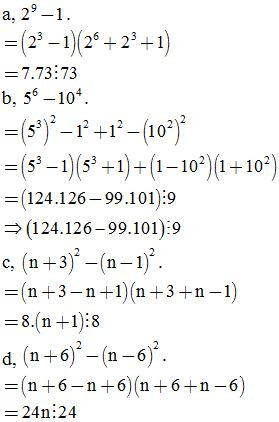
Bài 15: Tính nhanh

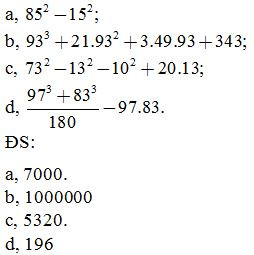
Bài 16: Phân tích các đa thức sau thành nhân tử:

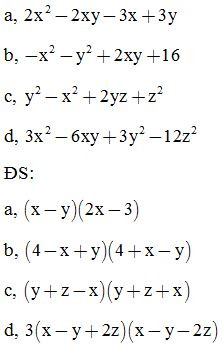
Bài 17: Phân tích các đa thức sau thành nhân tử:

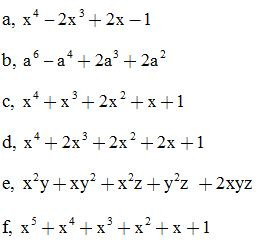
ĐS:

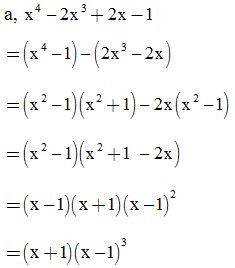
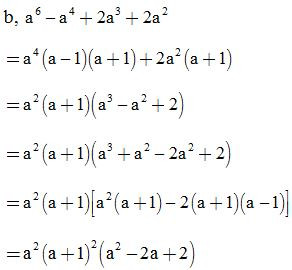
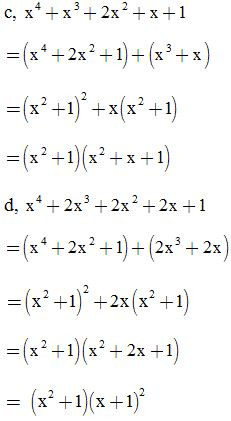
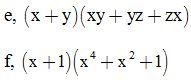
Bài 18: Phân tích đa thức thành nhân tử rồi tính giá trị của biểu thức:

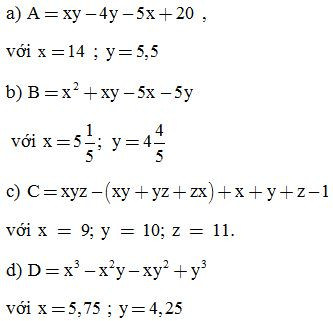
ĐS:

a, A = 5

b, B = 2

c, C = 720

d, D = 22,5

Bài 19: Tính nhanh

a, 9³ - 9² .(-1) - 9.11 + (-1).11

b, 2016.2017 - 2017²

ĐS:

a, 700

b, - 1

Bài 20: Tìm x biết

a, $3x^4-9x^3$$=-9x^2+27x$

b, $x^2\left(x+8\right)+x^2=-8x$

ĐS:

a, x = 0, x = 3

b, x = -8, x = -1, x = 0

Bài 21: Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)

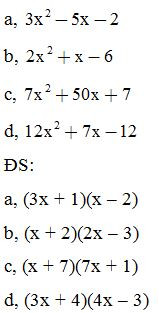
Bài 22: Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)

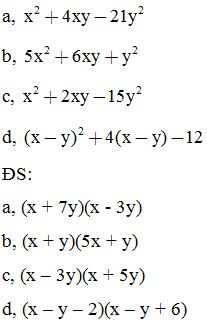
Bài 23: Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)

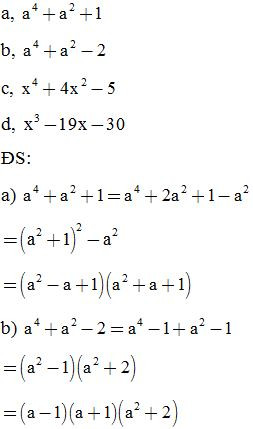
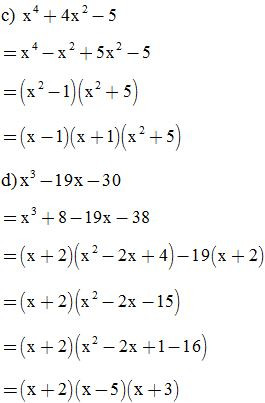
Bài 24: Phân tích các đa thức sau thành nhân tử: (thêm bớt cùng một hạng tử)

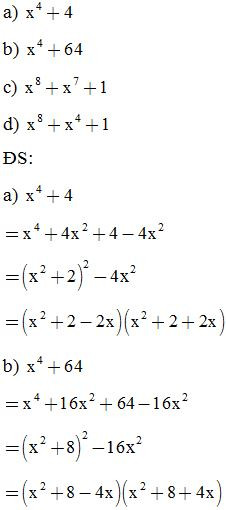
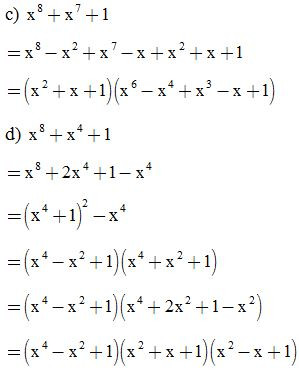
Bài 25: Phân tích các đa thức sau thành nhân tử: (đặt biến phụ)

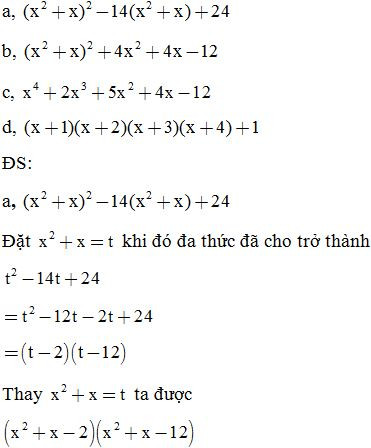
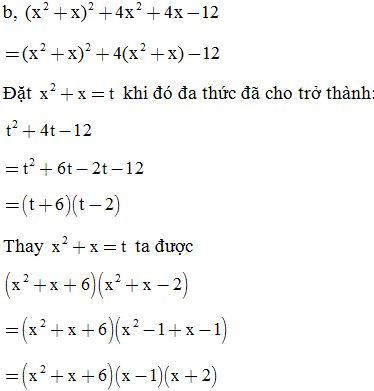
Bài 26: Phân tích các đa thức sau thành nhân tử: (đặt biến phụ)

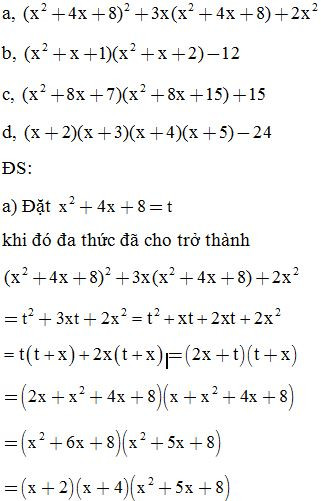
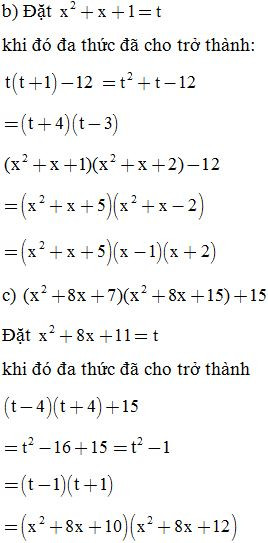
Bài 27: Tìm x biết:

a, $x^2–10x+16=0$

b, $x^2–11x–26=0$

c, $2x^2+7x–4=0$

ĐS:

a, x= 8, x = 2

b, x = -2, x =13

c, x = -4, x = $\frac{1}{2}$

Bài 28: Tìm x biết:

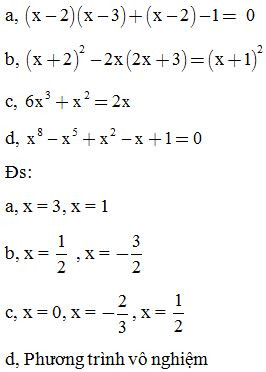
Bài 29: Chứng minh với mọi số nguyên n thì $A=n^4-2n^3-n^2+2n$ chia hết cho 24.

ĐS:

Gợi ý: $A=\left(n-2\right)\left(n^3-n\right)$$=\left(n-2\right)\left(n-1\right)n\left(n+1\right)$

A là tích của 4 số tự nguyên liên tiếp nên A chia hết cho 2, cho 3 và cho 4. Vì (2;3)=1 nên A chia hết cho 6. Suy ra A chia hết cho 4.6=24

Bài 30:

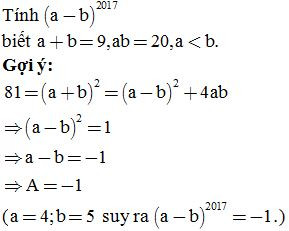
Xem thêm các dạng bài tập Toán lớp 8 có đáp án và lời giải chi tiết khác:

Cách chia đơn thức cho đơn thức, chia đa thức cho đơn thức chi tiết

Cách chia đa thức một biến đã sắp xếp lớp 8 và cách giải

Góc trong tứ giác và cách giải các dạng bài tập

Hình thang, hình thang vuông, hình thang cân lớp 8 và cách giải

Đối xứng trục, đối xứng tâm lớp 8 và cách giải bài tập