Trắc nghiệm Công thức lượng giác (có đáp án)
Trắc nghiệm Toán 10 Bài 3: Công thức lượng giác
-
2091 lượt thi
-
28 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 4:
14/12/2024Biểu thức có giá trị đúng bằng :
 Xem đáp án
Xem đáp án
Đáp án đúng là : A
Lời giải.
*Phương pháp giải:
Sử dụng công thức lượng giác
*Lý thuyết:
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm
Lý thuyết Công thức lượng giác – Toán 11 Kết nối tri thứcCâu 5:
06/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : C
Lời giải.
*Phương pháp giải:
Sử dụng công thức chu kì và hai góc phụ nhau, bù nhaun để tính giá trị của biểu thức.
*Lý thuyết:
Đối với hai góc bù nhau, α và 180° – α, ta có:
sin (180° – α) = sin α;
cos (180° – α) = - cos α;
tan (180° – α) = - tan α (α ≠ 90°);
cot (180° – α) = - cot α (0° < α < 180°).
Chú ý:
- Hai góc bù nhau có sin bằng nhau ; có côsin , tang, côtang đối nhau.
Xem thêm
Tổng hợp lý thuyết Chương 3 – Toán 10 Kết nối tri thức
Câu 7:
06/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : D
Lời giải.
*Phương pháp giải:
Sử dụng công thức lượng giác cơ bản Tan x =Sinx/cos x
*Lý thuyết:
1. Công thức lượng giác cơ bản
Xem thêm
Tổng hợp bảng giá trị lượng giác (2024) đầy đủ, chi tiết nhất
Câu 9:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
Suy ra .
Câu 10:
25/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng: B
* Lời giải:
.
suy ra
* Phương pháp giải:
- áp dụng công thức lượng giác tan(a+b) để tính toán ra giá trị của a + b
* Lý thuyết cần nắm thêm về công thức lượng giác:
1. Công thức cộng lượng giác
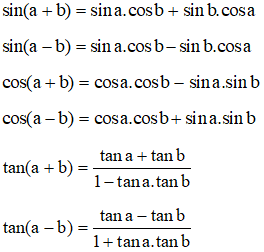
2. Công thức nhân, hạ bậc lượng giác
* Công thức nhân đôi:
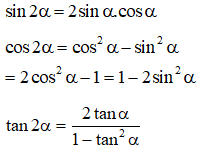
* Công thức hạ bậc:
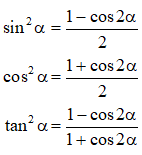
* Công thức nhân ba:
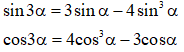
3. Công thức biến đổi tích thành tổng
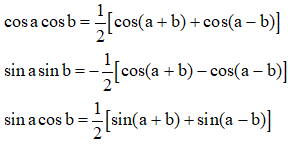
4. Công thức biển đổi tổng thành tích

5. Công thức nghiệm của phương trình lượng giác
a) Phương trình lượng giác cơ bản
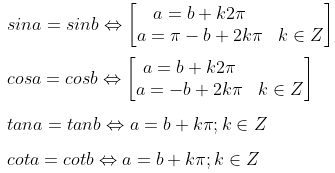
b) Phương trình lượng giác đặc biệt
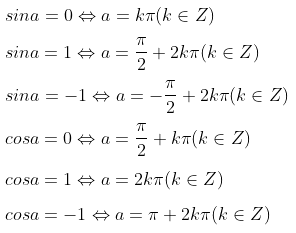
Các dạng bài tập lượng giác
Dạng 1: Tính giá trị lượng giác của góc đặc biệt
a. Phương pháp giải:
- Sử dụng định nghĩa giá trị lượng giá của một góc.
- Sử dụng tính chất và bảng giá trị lượng giác đặc biệt.
- Sử dụng các công thức lượng giác.
Dạng 2: Chứng minh đẳng thức lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Dùng hệ thức lượng giác biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
Xem thêm các bài viết liên quan hay, chi tiết:
Công thức lượng giác (2024) và cách giải bài tập chi tiết nhất
Câu 11:
05/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng: B
* Phương pháp giải:
- Áp dụng công thức lượng giác cơ bản: tanx.cotx = 1 để đưa cotx, coty thành tanx và tany
- Áp dụng công thức cộng lượng giác về tan: tan(x+y) =
- Thay giá trị tanx và tan y ở phía trên vào công thức để tính ra giá trị
* Lời giải:
Ta có: tan (x+y) =
(1)
Ta lại có:
tanx.cotx = 1 mà cotx = nên tanx =
tany.coty = 1 mà coty = nên tany = 7
Thay vào (1) ta được:
tan(x + y) =
x + y =
Vậy giá trị x + y =
* Các dạng bài tập lượng giác lớp 10
a) Dạng 1: Tính giá trị lượng giác của góc đặc biệt
* Phương pháp giải:
+ Sử dụng định nghĩa giá trị lượng giá của một góc.
+ Sử dụng tính chất và bảng giá trị lượng giác đặc biệt.
+ Sử dụng các công thức lượng giác.
b) Dạng 2: Chứng minh đẳng thức lượng giác
* Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
+ Cách 1: Dùng hệ thức lượng giác biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
+ Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
+ Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
c) Dạng 3: Thu gọn biểu thức lượng giác
* Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
d) Dạng 4: Tính giá trị biểu thức
* Phương pháp giải:
Sử dụng hệ thức cơ bản, các công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt.
Xem thêm các bài viết liên quan hay, chi tiết:
TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án 2023) – Toán 11
TOP 12 câu Trắc nghiệm Công thức lượng giác (Kết nối tri thức 2024) có đáp án - Toán 11
Câu 12:
23/07/2024Cho , giá trị có thể nhận giá trị nào dưới đây:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
Câu 13:
15/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : C
Ta có:
→ C đúng.A,B,D sai.
* Giá trị lượng giác của một góc từ 0° đến 180°
1.1 Định nghĩa
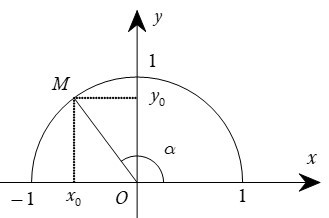
Với mỗi góc α (0 ≤ α ≤ 180°) ta xác định một điểm M (x0, y0) trên nửa đường tròn
đơn vị sao cho góc = α. Khi đó ta có định nghĩa:
+) sin của góc α, kí hiệu là sinα, được xác định bởi: sinα = y0;
+) côsin của góc α, kí hiệu là cosα, được xác định bởi: cosα = x0;
+) tang của góc α, kí hiệu là tanα, được xác định bởi: tanα = (x0 ≠ 0);
+) côtang của góc α, kí hiệu là cotα, được xác định bởi: cotα = (y0 ≠ 0).
Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.
Chú ý:
tanα = (α ≠ 90°);
cotα = (0 < α < 180°).
sin(90° – α) = cosα (0° ≤ α ≤ 90°);
cos(90° – α) = sinα (0° ≤ α ≤ 90°);
tan(90° – α) = cotα (0° ≤ α ≤ 90°);
cot(90° – α) = tanα (0° ≤ α ≤ 90°).
1.2. Tính chất
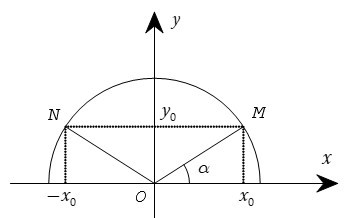
Trên hình bên ta có dây cung NM song song với trục Ox và nếu = α thì = 180o – α. Với 0° ≤ α ≤ 180° thì:
sin(180° – α) = sinα,
cos(180° – α) = – cosα,
tan(180° – α) = – tanα (α ≠ 90°),
cot(180° – α) = – cotα (α ≠ 0°, α ≠ 180°).
Xem thêm các bài viết liên quan,chi tiết khác:
Câu 14:
12/09/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
Ta có:
* Giải thích
1. Đồ thị và tính chất của hàm số y = cosx
Tập xác định là .
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2.
Đồng biến trên mỗi khoảng và nghịch biến trên mỗi khoảng .
Có đồ thị là một đường hình sin đối xứng qua trục tung.
Câu 15:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
Công thức đúng là
Câu 16:
04/09/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Giải thích:
Lời giải.
Ta có:
* Công thức lượng giác:
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
2. Định lí sin
Trong tam giác ABC:

Xem thêm các bài viết liên quan hay, chi tiết khác:
Lý thuyết Toán 10 Bài 6. Hệ thức lượng trong tam giác – Kết nối tri thức
Giải sách bài tập Toán lớp 10 Bài 6: Hệ thức lượng trong tam giác - Kết nối tri thức
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
Ta có :
Câu 18:
23/07/2024Biết và theo thứ tự lập thành một cấp số cộng. Tích số bằng :
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
Ta có:
suy ra:
Câu 19:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
Ta có :
Câu 20:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
Ta có:
Câu 21:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
Ta có
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
Ta có
Câu 25:
12/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : A
Lời giải.
Ta có :
*Phương pháp giải:
Áp dụng công thức lượng giác
*Lý thuyết:
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm
Lý thuyết Công thức lượng giác – Toán 11 Kết nối tri thứcCâu 27:
06/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : D
Lời giải.
Ta có :
*Phương pháp giải:
-Áp dụng công thức hạ bậc :
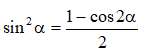
*Lý thuyết:
1. Công thức cộng lượng giác
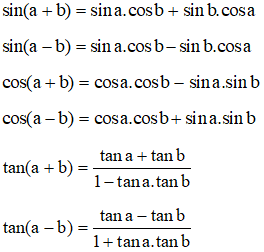
2. Công thức nhân, hạ bậc lượng giác
* Công thức nhân đôi:
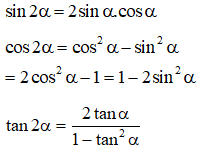
* Công thức hạ bậc:
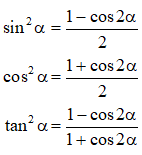
* Công thức nhân ba:
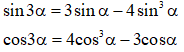
3. Công thức biến đổi tích thành tổng
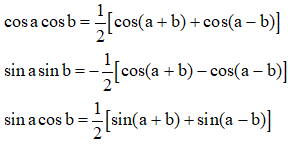
4. Công thức biển đổi tổng thành tích

5. Công thức nghiệm của phương trình lượng giác
a) Phương trình lượng giác cơ bản
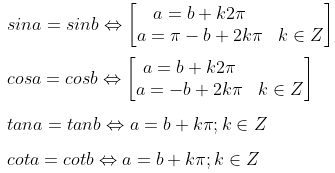
b) Phương trình lượng giác đặc biệt
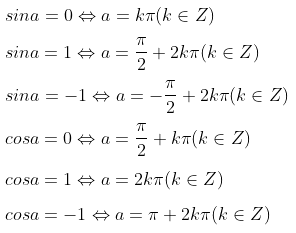
6. Bảng xét dấu của các giá trị lượng giác
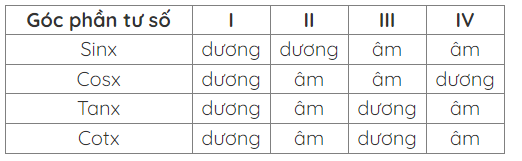
7. Bảng giá trị lương giác của các góc đặc biệt
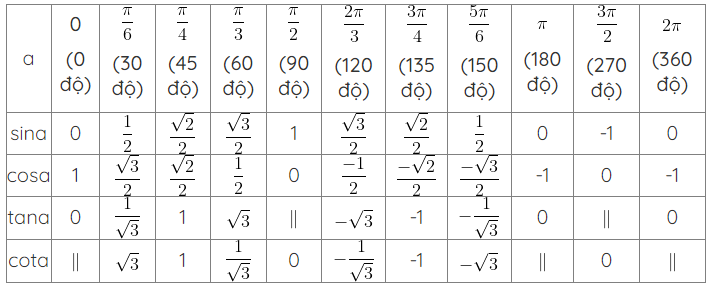
Xem thêm
Công thức lượng giác (2024) và cách giải bài tập chi tiết nhấtCó thể bạn quan tâm
- Trắc nghiệm Công thức lượng giác (có đáp án) (2090 lượt thi)
- Trắc nghiệm Công thức lượng giác có đáp án (348 lượt thi)
- Trắc nghiệm Công thức lượng giác có đáp án (Nhận biết) (443 lượt thi)
- Trắc nghiệm Công thức lượng giác có đáp án (Thông hiểu) (290 lượt thi)
- Trắc nghiệm Công thức lượng giác có đáp án (Vận dụng) (334 lượt thi)
- Trắc nghiệm Công thức lượng giác có đáp án (Tổng hợp) (332 lượt thi)
Các bài thi hot trong chương
- 100 câu trắc nghiệm Cung và góc lượng giác nâng cao (1826 lượt thi)
- 100 câu trắc nghiệm Cung và góc lượng giác cơ bản (1405 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một cung (có đáp án) (1213 lượt thi)
- Trắc nghiệm Cung và góc lượng giác (có đáp án) (832 lượt thi)
- Trắc nghiệm Ôn tập chương 6 (có đáp án) (617 lượt thi)
- Trắc nghiệm: Giá Trị lượng giác của một cung có đáp án (506 lượt thi)
- Trắc nghiệm Giá trị có lượng giác của một cung có đáp án (501 lượt thi)
- Trắc nghiệm Góc và cung lượng giác có đáp án (493 lượt thi)
- Trắc nghiệm Ôn tập chương 6 Cung và góc lượng giác công thức lượng giác có đáp án (486 lượt thi)
- Trắc nghiệm Cung và góc lượng giác có đáp án (Nhận biết) (450 lượt thi)
