100 câu trắc nghiệm Cung và góc lượng giác cơ bản
100 câu trắc nghiệm Cung và góc lượng giác cơ bản (P2)
-
1512 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Cho .Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn A.
Ta có nên điểm cuối của cung α thuộc góc phần tư thứ I.
Câu 2:
10/10/2024Cho .Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: D.
*Phương pháp giải:
- Ta trừ cả 3 vế cho để tìm ra điểm cuối rồi xét xem điểm cuối đang ở góc phần tư nào trong đường tròn lượng giác để xét dấu
*Lời giải:
Ta có
Do đó; điểm cuối cùng α – π thuộc góc phần tư thứ 3 nên sin(α – π) < 0.
*Một số dạng bài/lý thuyết cần nắm thêm:
a. Đơn vị đo góc và cung tròn, độ dài cung tròn:
* Đơn vị rađian: Cung tròn có độ dài bằng bán kính gọi là cung có số đo 1 rađian, gọi tắt là cung 1 rađian. 1 rađian còn viết tắt là 1 rad.
Vì tính thông dụng của đơn vị rađian người ta thường không viết rađian hay rad sau số đo của cung và góc.
* Độ dài cung tròn. Quan hệ giữa độ và rađian:
180o=πrad suy ra 1o=π180rad và1rad=(180π)o
* Độ dài cung tròn
Một cung của đường tròn bán kính R có số đo αrad thì độ dài l=Rα.
b. Góc và cung lượng giác:
* Đường tròn định hướng: Đường tròn định hướng là một đường tròn trên đó ta đã chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại gọi là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ gọi là chiều dương (cùng chiều kim đồng hồ là chiều âm).
Dạng 1.1: Cách đổi độ sang rađian và rađian sang độ
* Phương pháp giải: + Đổi độ sang rađian:
Áp dụng lý thuyết: 1o=π180rad, ta suy ra: αo=α.π180rad.
+ Đổi rađian sang độ:
Áp dụng lý thuyết: 1rad=(180π)o, ta suy ra βrad=(β.180π)o
Dạng 1.2: Cách tính độ dài cung tròn
* Phương pháp giải: Áp dụng công thức: l=Rα, trong đó: l là độ dài cung tròn, R là bán kính đường tròn,α là số đo bằng rad của cung.
Trường hợp α có số đo bằng độ, ta có công thức: l=R.π.α180
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Cung và góc lượng giác có đáp án – Toán lớp 10
Câu 3:
22/11/2024Cho .Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: D.
* Lời giải:
Ta có :
* Phương pháp giải:
-Sử dụng bảng dấu giá trị lượng giác và giá trị lượng giác các góc đặc biệt để xét:
Bảng xác định dấu của các giá trị lượng giác
| Giá trị lượng giác |Góc phần tư | I | II | III | IV |
| cos α | + | - | - | + |
| sin α | + | + | - | - |
| tan α | + | - | + | - |
| cot α | + | - | + | - |
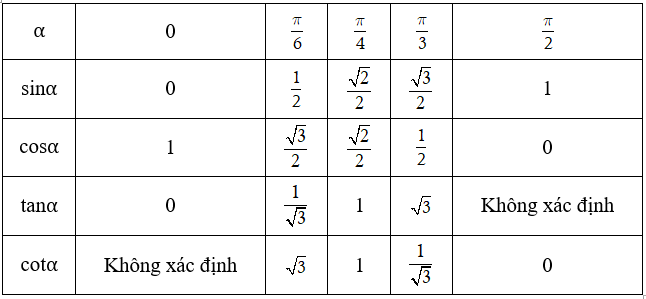
Giá trị lượng giác của các cung đặc biệt
*Một số lý thuyết và dạng bài tập về giá trị lượng giác của một cung:
1. Đồ thị và tính chất của hàm số y = sinx
- Tập xác định là R.
- Tập giá trị là [-1;1].
- Là hàm số lẻ và tuần hoàn chu kì 2π.
- Đồng biến trên mỗi khoảng (−π2+k2π;π2+k2π) và nghịch biến trên mỗi khoảng (π2+k2π;3π2+k2π)
- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
2. Đồ thị và tính chất của hàm số y = cosx
Tập xác định là R.
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2π.
Đồng biến trên mỗi khoảng (−π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π;π+k2π).
Có đồ thị là một đường hình sin đối xứng qua trục tung.
Hệ quả:
+) sinα,cosα xác định với mọi giá trị của α và −1≤sinα≤1,−1≤cosα≤1.
+) tanα được xác định khi α≠π2+kπ, xác định khi α≠kπ
+) sinα=sin(α+k2π),cosα=cos(α+k2π)
tanα=tan(α+kπ),cotα=cot(α+kπ)
+) Dấu của các giá trị lượng giác phụ thuộc vào vị trí điểm M nằm trên đường tròn lượng giác.
Ta có bảng xác định dấu của các giá trị lượng giác:
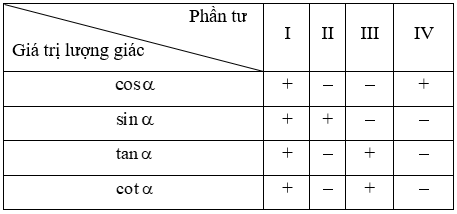
Các công thức lượng giác cơ bản:

Các dạng bài
Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị
a. Phương pháp giải:
Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.
Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
Dạng 3: Rút gọn biểu thức lượng giác
a. Phương pháp giải:
Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
Xem thêm các bài viết liên quan hay, chi tiết
Toán 10 Bài 2 giải vở bài tập: Giá trị lượng giác của một cung
Câu 4:
22/11/2024Cho Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: B.
* Lời giải:
Ta có
Nên suy ra
* Phương pháp giải:
-Sử dụng bảng dấu giá trị lượng giác và giá trị lượng giác các góc đặc biệt để xét:
Bảng xác định dấu của các giá trị lượng giác
| Giá trị lượng giác |Góc phần tư | I | II | III | IV |
| cos α | + | - | - | + |
| sin α | + | + | - | - |
| tan α | + | - | + | - |
| cot α | + | - | + | - |
Giá trị lượng giác của các cung đặc biệt
*Một số lý thuyết và dạng bài tập về giá trị lượng giác của một cung:
1. Đồ thị và tính chất của hàm số y = sinx
- Tập xác định là RRR.
- Tập giá trị là [-1;1].
- Là hàm số lẻ và tuần hoàn chu kì 2πππ.
- Đồng biến trên mỗi khoảng (−π2+k2π;π2+k2π)(−π2+k2π;π2+k2π)(−π2+k2π;π2+k2π) và nghịch biến trên mỗi khoảng (π2+k2π;3π2+k2π)(π2+k2π;3π2+k2π)(π2+k2π;3π2+k2π)
- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
2. Đồ thị và tính chất của hàm số y = cosx
Tập xác định là RRR.
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2πππ.
Đồng biến trên mỗi khoảng (−π+k2π;k2π)(−π+k2π;k2π)(−π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π;π+k2π)(k2π;π+k2π)(k2π;π+k2π).
Có đồ thị là một đường hình sin đối xứng qua trục tung.
Hệ quả:
+) sinα,cosαsinα,cosαsinα,cosα xác định với mọi giá trị của ααα và −1≤sinα≤1,−1≤cosα≤1−1≤sinα≤1,−1≤cosα≤1−1≤sinα≤1,−1≤cosα≤1.
+) tanαtanαtanα được xác định khi α≠π2+kπα≠π2+kπα≠π2+kπ, xác định khi α≠kπα≠kπα≠kπ
+) sinα=sin(α+k2π),cosα=cos(α+k2π)sinα=sin(α+k2π),cosα=cos(α+k2π)sinα=sin(α+k2π),cosα=cos(α+k2π)
tanα=tan(α+kπ),cotα=cot(α+kπ)tanα=tan(α+kπ),cotα=cot(α+kπ)tanα=tan(α+kπ),cotα=cot(α+kπ)
+) Dấu của các giá trị lượng giác phụ thuộc vào vị trí điểm M nằm trên đường tròn lượng giác.
Ta có bảng xác định dấu của các giá trị lượng giác:

Các công thức lượng giác cơ bản:

Các dạng bài
Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị
a. Phương pháp giải:
Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.
Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
Dạng 3: Rút gọn biểu thức lượng giác
a. Phương pháp giải:
Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
Xem thêm các bài viết liên quan hay, chi tiết
Toán 10 Bài 2 giải vở bài tập: Giá trị lượng giác của một cung
Câu 5:
18/10/2024Cho .Khi đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là C
*Phương pháp giải
sin( a - b ) = sin a cos b - cos a sin b
*Lời giải
Cách 1:
Cách 2:
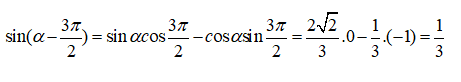
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180°
Tổng hợp bảng giá trị lượng giác
Câu 8:
27/11/2024Cho góc α thỏa mãn và .Tính cosα.
 Xem đáp án
Xem đáp án
Đáp án đúng là C.
Lời giải
Ta có
*Phương pháp giải:
Sử dụng công thức sin bình cộng cos bình bằng 1
*Lý thuyết:
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Câu 9:
22/07/2024Cho đường tròn có bán kính 6cm . Tìm số đo (rad) của cung có độ dài là 3cm :
 Xem đáp án
Xem đáp án
Chọn A.
Theo công thức tính độ dài cung tròn ta có nên
Ta có .
Câu 10:
18/07/2024Cung của đường tròn có bán kính 8,43cm có số đó bằng 3,85 rad có độ dài xấp xỉ bằng bao nhiêu? (làm tròn kết quả đến hàng phần chục)
 Xem đáp án
Xem đáp án
Chọn D.
Theo công thức tính độ dài cung ta có độ dài cung có số đo 3,85 rad là
l = R.α = 8,43.3,85 = 32,4555 cm.
Câu 11:
17/07/2024Xét góc lượng giác (OA; OM) = α, trong đó M là điểm không nằm trên các trục tọa độ Ox và Oy. Khi đó M thuộc góc phần tư nào để sinα và cosα cùng dấu
 Xem đáp án
Xem đáp án
Chọn B.
Dựa theo định nghĩa các giá trị lượng giác trên đường tròn lượng giác.
Khi M nằm trong góc phần tư thứ nhất thì sin α và cosα cùng dương hoặc khi M nằm trong góc phần tư thứ ba thì sinα và cosα cùng âm.
Câu 12:
21/11/2024Cho α là góc tù. Điều khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: C.
* Lời giải:
Vì α là góc tù, nên sinα > 0 và cos α < 0 do đó tan α < 0 và cotα < 0.
* Phương pháp giải:
- Áp dụng bảng dấu của các giá trị lượng giác để xét dấu
* Lý thuyết cần nắm và dạng bài toán về cung và giá trị lượng giác:
Dấu của các giá trị lượng giác của góc α
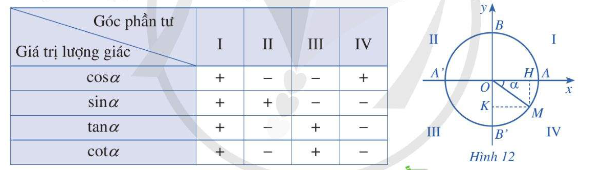
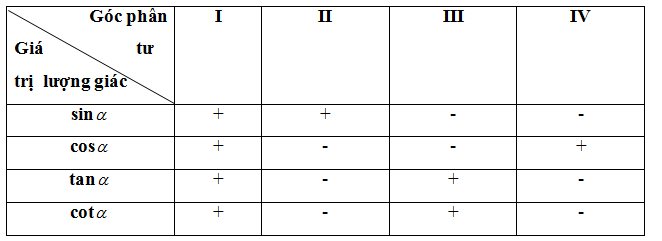
Công thức nhân đôi:
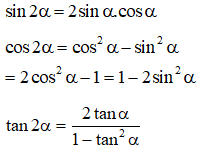
* Công thức hạ bậc:
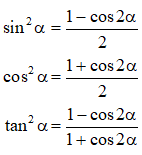
Phương trình lượng giác cơ bản
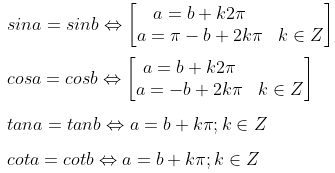
Phương trình lượng giác đặc biệt
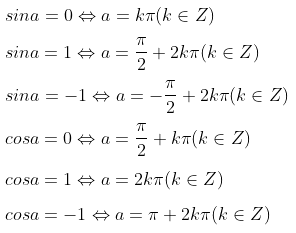
Xem thêm các bài viết liên quan hay, chi tiết:
Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất
TOP 40 câu Trắc nghiệm Tỉ số lượng giác của góc nhọn và Bảng lượng giác (có đáp án 2024) - Toán
Câu 13:
07/11/2024Cho góc α thỏa mãn và .Tính tanα.
 Xem đáp án
Xem đáp án
Đáp án đúng: B.
*Lời giải:
Ta có
*Phương pháp giải:
- áp dụng công thức cung lượng giác cơ bản:
sin2x + cos2x = 1
- Do từ đây ta sẽ tìm ra được sinx và tìm ra tanx
* Lý thuyết và các dạng bài về góc và cung lượng giác:
Công thức nhân đôi:
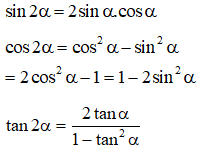
* Công thức hạ bậc:
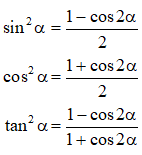
Phương trình lượng giác cơ bản
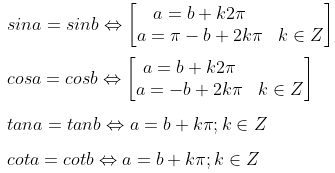
Phương trình lượng giác đặc biệt
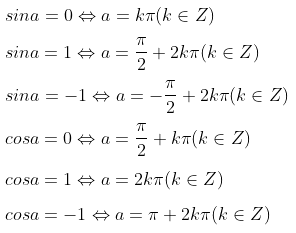
Xem thêm các bài viết liên quan hay, chi tiết:
Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất
Giải Toán 10 Chương 6: Cung và góc lượng giác. Công thức lượng giác
Câu 16:
27/11/2024Cho góc α thỏa sin α = 3/5 và 900 < α < 1800.Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là D.
Lời giải
Ta có
*Phương pháp giải:
Sử dụng công thức sin bình cộng cos bình bằng 1
*Lý thuyết:
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Câu 17:
23/07/2024Cho góc α thỏa cotα = và 00 < α < 900. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
Câu 18:
22/09/2024Cho cos α = 2/3. Tính giá trị của biểu thức
 Xem đáp án
Xem đáp án
Chọn D.
Ta có
Suy ra
* Một số công thức cần nhớ để áp dụng
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Câu 19:
26/12/2024Cho góc α thỏa mãn và .Tính .
 Xem đáp án
Xem đáp án
Đáp án đúng là C.
Lời giải
Ta có
Thay α = π vào P ta được
*Phương pháp giải:
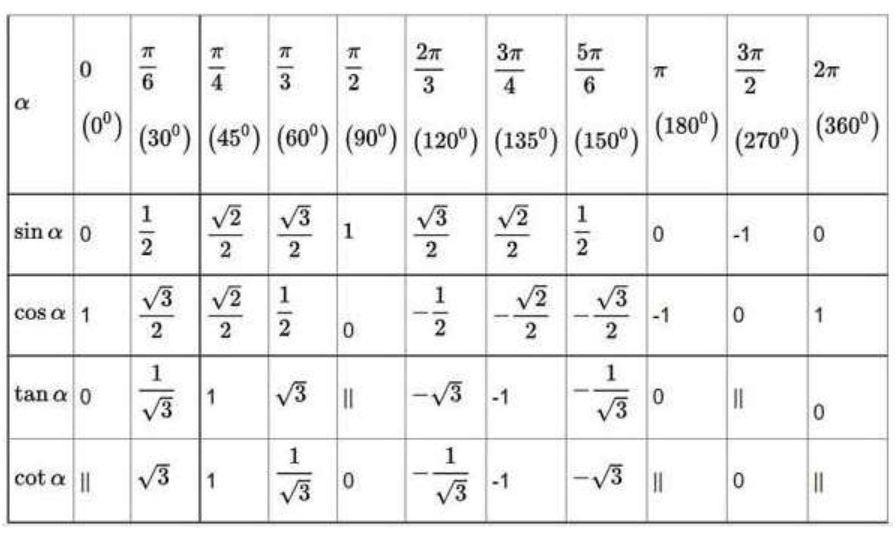
*Lý thuyết:
1. Công thức lượng giác cơ bản
2. Công thức cộng lượng giác
3. Công thức các cung liên kết trên đường tròn lượng giác
Mẹo nhớ: cos đối, sin bù, phụ chéo, tan hơn kém π
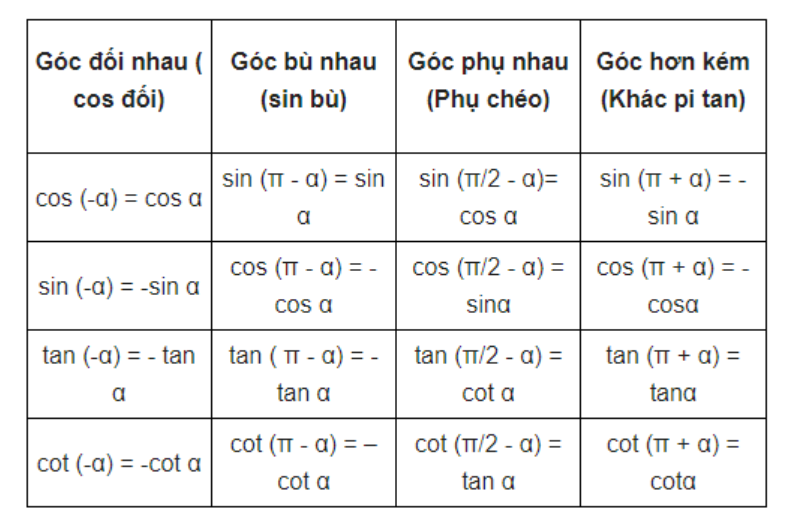
Cung hơn kém
+ cos( + x) = - sinx
+ sin( + x) = cosx
4. Công thức nhân
Công thức nhân đôi
Công thức nhân ba
Công thức nhân bốn
5. Công thức hạ bậc
Thực ra những công thức này đều được biến đổi ra từ công thức lượng giác cơ bản
Ví dụ như: sin2a=1 - cos2a = 1 - = .
6. Công thức biến đổi tổng thành tích
Xem thêm
Tổng hợp bảng giá trị lượng giác (2024) đầy đủ, chi tiết nhất
TOP 10 câu Trắc nghiệm Số đo góc. Các góc đặc biệt có đáp án
Câu 20:
23/07/2024Cho góc α thỏa mãn và Tính giá trị của biểu thức
 Xem đáp án
Xem đáp án
Chọn D.
Ta có
Thay vào P ta được
.
Câu 21:
27/11/2024Cho góc α thỏa mãn và .Tính
 Xem đáp án
Xem đáp án
Đáp án đúng là B.
Lời giải
Ta có
Suy ra cos α =- 3/5 và sinα = cosα.tanα = 4/5.
Thay sin α = 4/5 và cosα = -3/5 vào P, ta được P = 31/11.
*Phương pháp giải
Sử dụng công thức 1 phần 1+ tan bình bằng cos bình
*Lý thuyết:
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Câu 22:
20/07/2024Cho góc α thỏa mãn tanα = 2. Tính
 Xem đáp án
Xem đáp án
Chọn D.
Chia cả tử và mẫu của biểu thức P cho cosα ta được
Câu 23:
23/07/2024Cho góc α thỏa mãn cotα = 1/3 .Tính
 Xem đáp án
Xem đáp án
Chọn D.
Chia cả tử và mẫu của P cho sinα ta được
Câu 24:
23/07/2024Cho góc α thỏa mãn tanα + cotα = 5.Tính P = tan3α + cot3α
 Xem đáp án
Xem đáp án
Chọn B.
Ta có P = tan3α + cot3α = (tanα + cotα) 3 - 3tanα.cotα( tanα + cotα)
= 53 - 3.5 = 110
Câu 25:
18/07/2024Một đường tròn có bán kính .Tìm độ dài của cung có số đo π/2 trên đường tròn.
 Xem đáp án
Xem đáp án
Chọn B.
Độ dài của cung trên đường tròn được tính bằng công thức:
Bài thi liên quan
-
100 câu trắc nghiệm Cung và góc lượng giác cơ bản (P1)
-
25 câu hỏi
-
30 phút
-
-
100 câu trắc nghiệm Cung và góc lượng giác cơ bản (P3)
-
25 câu hỏi
-
30 phút
-
-
100 câu trắc nghiệm Cung và góc lượng giác cơ bản (P4)
-
25 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập chương 6 (có đáp án) (646 lượt thi)
- 100 câu trắc nghiệm Cung và góc lượng giác cơ bản (1511 lượt thi)
- 100 câu trắc nghiệm Cung và góc lượng giác nâng cao (1923 lượt thi)
- Trắc nghiệm Ôn tập chương 6 Cung và góc lượng giác công thức lượng giác có đáp án (514 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (Nhận biết) (279 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (Thông hiểu) (339 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (Vận dụng) (389 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 6 có đáp án (319 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Công thức lượng giác (có đáp án) (2157 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một cung (có đáp án) (1248 lượt thi)
- Trắc nghiệm Cung và góc lượng giác (có đáp án) (862 lượt thi)
- Trắc nghiệm Giá trị có lượng giác của một cung có đáp án (527 lượt thi)
- Trắc nghiệm: Giá Trị lượng giác của một cung có đáp án (526 lượt thi)
- Trắc nghiệm Góc và cung lượng giác có đáp án (515 lượt thi)
- Trắc nghiệm Cung và góc lượng giác có đáp án (Nhận biết) (486 lượt thi)
- Trắc nghiệm Công thức lượng giác có đáp án (Nhận biết) (469 lượt thi)
- Trắc nghiệm Giá trị có lượng giác của một cung có đáp án (Nhận biết) (460 lượt thi)
- Trắc nghiệm Cung và góc lượng giác có đáp án (Thông hiểu) (451 lượt thi)