Toán 11 Bài 2 (Kết nối tri thức): Công thức lượng giác

Giải Toán 11 Bài 2: Công thức lượng giác

Bài giảng Toán 11 Bài 2: Công thức lượng giác

Giải Toán 11 trang 17 Tập 1

Mở đầu trang 17 Toán 11 Tập 1: Một thiết bị trễ kĩ thuật số lặp lại tín hiệu đầu vào bằng cách lặp lại tín hiệu đó trong một khoảng thời gian cố định sau khi nhận được tín hiệu. Nếu một thiết bị như vậy nhận được nốt thuần f₁(t) = 5sin t và phát lại được nốt thuần f₂(t) = 5cos t thì âm kết hợp là f(t) = f₁(t) + f₂(t), trong đó t là biến thời gian. Chứng tỏ rằng âm kết hợp viết được dưới dạng f(t) = ksin (t + φ), tức là âm kết hợp là một sóng âm hình sin. Hãy xác định biên độ âm k và pha ban đầu φ (– π ≤ φ ≤ π) của sóng âm.

Lời giải:

Sau bài học này ta sẽ giải quyết được bài toán trên như sau:

Ta có: f(t) = = f₁(t) + f₂(t) = 5sin t + 5 cos t = 5(sin t + cos t)

Theo Ví dụ 2 trang 18 SGK Toán lớp 11 Tập 1, ta chứng minh được

sin t + cos t = $\sqrt{2}\sin \left(t+\frac{\pi }{4}\right)$.

Do đó, $f\left(t\right)=5\sqrt{2}\sin \left(t+\frac{\pi }{4}\right)$.

Vậy âm kết hợp viết được dưới dạng f(t) = ksin (t + φ), trong đó biên độ âm $k=5\sqrt{2}$ và pha ban đầu của sóng âm là $\phi =\frac{\pi }{4}$.

HĐ1 trang 17 Toán 11 Tập 1: Nhận biết công thức cộng

a) Cho $a=\frac{\pi }{4}$ và $b=\frac{\pi }{6}$, hãy chứng tỏ cos(a – b) = cos a cos b + sin a sin b.

b) Bằng cách viết a + b = a – (– b) và từ công thức ở HĐ1a, hãy tính cos(a + b).

c) Bằng cách viết sin(a – b) = $\cos \left[\frac{\pi }{2}-\left(a-b\right)\right]=\cos \left[\left(\frac{\pi }{2}-a\right)+b\right]$ và sử dụng công thức vừa thiết lập ở HĐ1b, hãy tính sin(a – b).

Lời giải:

a) Ta có: a – b = $\frac{\pi }{4}-\frac{\pi }{6}=\frac{\pi }{12}$ nên cos(a – b) = $\cos \frac{\pi }{12}=\frac{\sqrt{6}+\sqrt{2}}{4}$.

cos a cos b + sin a sin b

= $\cos \frac{\pi }{4}\cos \frac{\pi }{6}+\sin \frac{\pi }{4}\sin \frac{\pi }{6}=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot \frac{1}{2}$

$=\frac{\sqrt{6}}{4}+\frac{\sqrt{2}}{4}=\frac{\sqrt{6}+\sqrt{2}}{4}$.

Vậy cos(a – b) = cos a cos b + sin a sin b.

b) Ta có: cos(a + b) = cos[a – (– b)] = cos a cos(– b) + sin a sin(– b)

Mà cos(– b) = cos b, sin(– b) = – sin b (hai góc đối nhau).

Do đó, cos(a + b) = cos a cos b + sin a . (– sin b) = cos a cos b – sin a sin b.

c) Ta có: sin(a – b) = $\cos \left[\frac{\pi }{2}-\left(a-b\right)\right]=\cos \left[\left(\frac{\pi }{2}-a\right)+b\right]$

$=\cos \left(\frac{\pi }{2}-a\right)\cos b-\sin \left(\frac{\pi }{2}-a\right)\sin b$

$=\sin a\cos b-\cos a\sin b$ (do $\cos \left(\frac{\pi }{2}-a\right)=\sin a$, $\sin \left(\frac{\pi }{2}-a\right)=\cos a$).

Vậy sin(a – b) = sin a cos b – cos a sin b.

Giải Toán 11 trang 18 Tập 1

Luyện tập 1 trang 18 Toán 11 Tập 1: Chứng minh rằng:

a) sin x – cos x = $\sqrt{2}\sin \left(x-\frac{\pi }{4}\right)$;

b) $\tan \left(\frac{\pi }{4}-x\right)=\frac{1-\tan x}{1+\tan x}$$\left(x\ne \frac{\pi }{2}+k\pi ,x\ne \frac{3\pi }{4}+k\pi ,k\in \mathbb{Z}\right)$.

Lời giải:

a) Ta có: $VP=\sqrt{2}\sin \left(x-\frac{\pi }{4}\right)=\sqrt{2}\left(\sin x\cos \frac{\pi }{4}-\cos x\sin \frac{\pi }{4}\right)$

$=\sqrt{2}\sin x.\frac{\sqrt{2}}{2}-\sqrt{2}\cos x.\frac{\sqrt{2}}{2}=\sin x-\cos x=VT$ (đpcm).

b) Ta có: $VT=\tan \left(\frac{\pi }{4}-x\right)=\frac{\tan \frac{\pi }{4}-\tan x}{1+\tan \frac{\pi }{4}\tan x}=\frac{1-\tan x}{1+\tan x}=VP$$\left(do\tan \frac{\pi }{4}=1\right)$.

Vận dụng 1 trang 18 Toán 11 Tập 1: Giải bài toán trong tình huống mở đầu.

Lời giải:

Ta có: f(t) = = f₁(t) + f₂(t) = 5sin t + 5 cos t = 5(sin t + cos t)

Theo Ví dụ 2 trang 18 SGK Toán lớp 11 Tập 1, ta chứng minh được

sin t + cos t = $\sqrt{2}\sin \left(t+\frac{\pi }{4}\right)$.

Do đó, $f\left(t\right)=5\sqrt{2}\sin \left(t+\frac{\pi }{4}\right)$.

Vậy âm kết hợp viết được dưới dạng f(t) = ksin (t + φ), trong đó biên độ âm $k=5\sqrt{2}$ và pha ban đầu của sóng âm là $\phi =\frac{\pi }{4}$.

HĐ2 trang 18 Toán 11 Tập 1: Xây dựng công thức nhân đôi

Lấy b = a trong các công thức cộng, hãy tìm công thức tính: sin 2a; cos 2a; tan 2a.

Lời giải:

Ta có:

+) sin 2a = sin(a + a) = sin a cos a + cos a sin a = sin a cos a + sin a cos a = 2 sin a cos a.

+) cos 2a = cos (a + a) = cos a cos a – sin a sin a = cos² a – sin² a

Mà sin² a + cos² a = 1, suy ra sin² a = 1 – cos² a và cos² a = 1 – sin² a.

Do đó, cos 2a = cos² a – sin² a = 2cos² a – 1 = 1 – 2sin² a.

+) tan 2a = tan (a + a) = $\frac{\tan a+\tan a}{1-\tan a\tan a}=\frac{2\tan a}{1-{\tan }^{2}a}$.

Giải Toán 11 trang 19 Tập 1

Luyện tập 2 trang 19 Toán 11 Tập 1: Không dùng máy tính, tính $\cos \frac{\pi }{8}$.

Lời giải:

Ta có: $\frac{\sqrt{2}}{2}=\cos \frac{\pi }{4}=\cos \left(2.\frac{\pi }{8}\right)=2{\cos }^2\frac{\pi }{8}-1$.

Suy ra $2{\cos }^2\frac{\pi }{8}=1+\frac{\sqrt{2}}{2}$. Do đó, ${\cos }^2\frac{\pi }{8}=\frac{2+\sqrt{2}}{4}$.

Vì $\cos \frac{\pi }{8}>0$ nên suy ra $\cos \frac{\pi }{8}=\frac{\sqrt{2+\sqrt{2}}}{2}$.

HĐ3 trang 19 Toán 11 Tập 1: Xây dựng công thức biến đổi tích thành tổng

a) Từ các công thức cộng cos(a + b) và cos(a – b), hãy tìm: cos a cos b; sin a sin b.

b) Từ các công thức cộng sin(a + b) và sin(a – b), hãy tìm: sin a cos b.

Lời giải:

a) Ta có: cos(a + b) = cos a cos b – sin a sin b (1);

cos(a – b) = cos a cos b + sin a sin b (2).

Lấy (1) và (2) cộng vế theo vế, ta được: cos(a + b) + cos(a – b) = 2cos a cos b.

Từ đó suy ra, cos a cos b = $\frac{1}{2}$[cos(a + b) + cos(a – b)].

Lấy (2) trừ vế theo vế cho (1), ta được: cos(a – b) – cos(a + b) = 2sin a sin b.

Từ đó suy ra, sin a sin b = $\frac{1}{2}$[cos(a – b) – cos(a + b)].

b) Ta có: sin(a + b) = sin a cos b + cos a sin b (3);

sin(a – b) = sin a cos b – cos a sin b (4).

Lấy (3) và (4) cộng vế theo vế, ta được: sin(a + b) + sin(a – b) = 2sin a cos b.

Từ đó suy ra, sin a cos b = $\frac{1}{2}$[sin(a + b) + sin(a – b)].

Luyện tập 3 trang 19 Toán 11 Tập 1: Không dùng máy tính, tính giá trị của các biểu thức:

A = cos 75° cos 15°; B = $\sin \frac{5\pi }{12}\cos \frac{7\pi }{12}$.

Lời giải:

Ta có:

A = cos 75° cos 15° = $\frac{1}{2}$[cos(75° – 15°) + cos(75° + cos 15°)]

= $\frac{1}{2}$(cos 60° + cos 90°) = $\frac{1}{2}\left(\frac{1}{2}+0\right)=\frac{1}{4}$.

B = $\sin \frac{5\pi }{12}\cos \frac{7\pi }{12}$ = $\frac{1}{2}\left[\sin \left(\frac{5\pi }{12}-\frac{7\pi }{12}\right)+\sin \left(\frac{5\pi }{12}+\frac{7\pi }{12}\right)\right]$

$=\frac{1}{2}\left[\sin \left(-\frac{\pi }{6}\right)+\sin \pi \right]=\frac{1}{2}\left(-\sin \frac{\pi }{6}+\sin \pi \right)$$=\frac{1}{2}\left(-\frac{1}{2}+0\right)=-\frac{1}{4}$.

Giải Toán 11 trang 20 Tập 1

HĐ4 trang 20 Toán 11 Tập 1: Xây dựng công thức biến đổi tổng thành tích

Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt u = a – b, v = a + b và viết các công thức nhận được.

Lời giải:

Ta có: cos a cos b = $\frac{1}{2}$[cos(a – b) + cos(a + b)] (1);

sin a sin b = $\frac{1}{2}$[cos(a – b) – cos(a + b)] (2);

sin a cos b = $\frac{1}{2}$[sin(a – b) + sin(a + b)] (3).

Đặt u = a – b, v = a + b.

Ta có: u + v = (a – b) + (a + b) = 2a và u – v = (a – b) – (a + b) = – 2b.

Suy ra, $a=\frac{u+v}{2},b=-\frac{u-v}{2}$.

Khi đó:

+) (1) trở thành $\cos \frac{u+v}{2}\cos \left(-\frac{u-v}{2}\right)=\frac{1}{2}\left(\cos u+\cos v\right)$

$\iff \cos u+\cos v=2\cos \frac{u+v}{2}\cos \frac{u-v}{2}$ (do $\cos \left(-\frac{u-v}{2}\right)=\cos \frac{u-v}{2}$).

+) (2) trở thành $\sin \frac{u+v}{2}\sin \left(-\frac{u-v}{2}\right)=\frac{1}{2}\left(\cos u-\cos v\right)$

$\iff \cos u-\cos v=-2\sin \frac{u+v}{2}\sin \frac{u-v}{2}$ (do $\sin \left(-\frac{u-v}{2}\right)=-\sin \frac{u-v}{2}$).

+) (3) trở thành $\sin \frac{u+v}{2}\cos \left(-\frac{u-v}{2}\right)=\frac{1}{2}\left(\sin u+\sin v\right)$

$\iff \sin u+\sin v=2\sin \frac{u+v}{2}\cos \frac{u-v}{2}$.

Luyện tập 4 trang 20 Toán 11 Tập 1: Không dùng máy tính, tính giá trị của biểu thức

$B = \cos \frac{\pi }{9}+\cos \frac{5\pi }{9}+\cos \frac{11\pi }{9} .$

Lời giải:

Ta có: B = $\cos \frac{\pi }{9}+\cos \frac{5\pi }{9}+\cos \frac{11\pi }{9}$

$=\left(\cos \frac{\pi }{9}+\cos \frac{11\pi }{9}\right)+\cos \frac{5\pi }{9}$

$=2\cos \frac{\frac{\pi }{9}+\frac{11\pi }{9}}{2}\cos \frac{\frac{\pi }{9}-\frac{11\pi }{9}}{2}+\cos \frac{5\pi }{9}$

$=2\cos \frac{2\pi }{3}\cos \left(-\frac{5\pi }{9}\right)+\cos \frac{5\pi }{9}$

$=2\cos \frac{2\pi }{3}\cos \frac{5\pi }{9}+\cos \frac{5\pi }{9}$

$=2.\left(-\frac{1}{2}\right)\cos \frac{5\pi }{9}+\cos \frac{5\pi }{9}$

$=-\cos \frac{5\pi }{9}+\cos \frac{5\pi }{9}=0$.

Vận dụng 2 trang 20 Toán 11 Tập 1: Khi nhấn một phím trên điện thoại cảm ứng, bàn phím sẽ tạo ra hai âm thuần, kết hợp với nhau để tạo ra âm thanh nhận dạng duy nhất phím. Hình 1.13 cho thấy tần số thấp f₁ và tần số cao f₂ liên quan đến mỗi phím. Nhấn một phím sẽ tạo ra sóng âm y = sin(2πf₁t) + sin(2πf₂t), ở đó t là biến thời gian (tính bằng giây).

a) Tìm hàm số mô hình hóa âm thanh được tạo ra khi nhấn phím 4.

b) Biến đổi công thức vừa tìm được ở câu a về dạng tích của một hàm số sin và một hàm số côsin.

Lời giải:

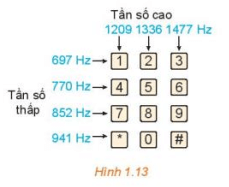
a) Quan sát Hình 1.13, ta nhận thấy khi nhấn phím 4, âm thanh được tạo ra có tần số thấp f₁ = 770 Hz và tần số cao f₂ = 1 209 Hz.

Khi đó, hàm số mô hình hóa âm thanh được tạo ra khi nhấn phím 4 là

y = sin(2π . 770t) + sin(2π . 1 209t) hay y = sin(1 540πt) + sin(2 418πt).

b) Ta có:

sin(1 540πt) + sin(2 418πt)

= $2\sin \frac{1540\pi t+2418\pi t}{2}\cos \frac{1540\pi t-2418\pi t}{2}$

= 2sin(1 979πt) cos(– 439πt)

= 2sin(1 979πt) cos(439πt).

Vậy ta có hàm số y = 2sin(1 979πt) cos(439πt).

Giải Toán 11 trang 21 Tập 1

Bài tập

Bài 1.7 trang 21 Toán 11 Tập 1: Sử dụng 15° = 45° – 30°, hãy tính các giá trị lượng giác của góc 15°.

Lời giải:

Ta có:

+) sin 15° = sin(45° – 30°) = sin 45° cos 30° – cos 45° sin 30°

= $\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}.\frac{1}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$.

+) cos 15° = cos(45° – 30°) = cos 45° cos 30° + sin 45° sin 30°

= $\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}.\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$.

+) tan 15° = tan(45° – 30°) = $\frac{\tan 45°-\tan 30°}{1+\tan 45°.\tan 30°}$ = $\frac{1-\frac{\sqrt{3}}{3}}{1+1.\frac{\sqrt{3}}{3}}=2-\sqrt{3}$.

+) cot 15° = $\frac{1}{\tan 15°}=\frac{1}{2-\sqrt{3}}=2+\sqrt{3}$.

Bài 1.8 trang 21 Toán 11 Tập 1: Tính:

a) $\cos \left(a+\frac{\pi }{6}\right)$, biết $\sin a=\frac{1}{\sqrt{3}}$ và $\frac{\pi }{2}<a<\pi$;

b) $\tan \left(a-\frac{\pi }{4}\right)$, biết $\cos a=-\frac{1}{3}$ và $\pi <a<\frac{3\pi }{2}$.

Lời giải:

a) Vì $\frac{\pi }{2}<a<\pi$ nên cos a < 0.

Mặt khác, từ sin² a + cos² a = 1 suy ra

cos a = $-\sqrt{1-{\sin }^{2}a}=-\sqrt{1-{\left(\frac{1}{\sqrt{3}}\right)}^2}=-\frac{\sqrt{6}}{3}$.

Ta có: $\cos \left(a+\frac{\pi }{6}\right)$$=\cos a\cos \frac{\pi }{6}-\sin a\sin \frac{\pi }{6}$

$=\left(-\frac{\sqrt{6}}{3}\right).\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{3}}.\frac{1}{2}=\frac{-\sqrt{6}-1}{2\sqrt{3}}=-\frac{\sqrt{3}+3\sqrt{2}}{6}$.

b) Vì $\pi <a<\frac{3\pi }{2}$ nên sin a < 0, do đó $\tan a=\frac{\sin a}{\cos a}>0$.

Mặt khác từ $1+{\tan }^{2}a=\frac{1}{{\cos }^{2}a}$

Suy ra $\tan a=\sqrt{\frac{1}{{\cos }^{2}a}-1}=\sqrt{\frac{1}{{\left(-\frac{1}{3}\right)}^2}-1}=2\sqrt{2}$.

Ta có: $\tan \left(a-\frac{\pi }{4}\right)$$=\frac{\tan a-\tan \frac{\pi }{4}}{1+\tan a\tan \frac{\pi }{4}}$$=\frac{2\sqrt{2}-1}{1+2\sqrt{2}.1}=\frac{9-4\sqrt{2}}{7}$.

Bài 1.9 trang 21 Toán 11 Tập 1: Tính sin 2a, cos 2a, tan 2a, biết:

a) $\sin a=\frac{1}{3}$ và $\frac{\pi }{2}<a<\pi$;

b) sin a + cos a = $\frac{1}{2}$ và $\frac{\pi }{2}<a<\frac{3\pi }{4}$.

Lời giải:

a) Vì $\frac{\pi }{2}<a<\pi$ nên cos a < 0.

Mặt khác, từ sin² a + cos² a = 1 suy ra

cos a = $-\sqrt{1-{\sin }^{2}a}=-\sqrt{1-{\left(\frac{1}{3}\right)}^2}=-\frac{2\sqrt{2}}{3}$.

Ta có: sin 2a = 2sin a cos a = $2.\frac{1}{3}.\left(-\frac{2\sqrt{2}}{3}\right)=-\frac{4\sqrt{2}}{9}$.

$\cos 2a=1-2{\sin }^{2}a=1-2.{\left(\frac{1}{3}\right)}^2=\frac{7}{9}$.

$\tan 2a=\frac{\sin 2a}{\cos 2a}=\frac{-\frac{4\sqrt{2}}{9}}{\frac{7}{9}}=-\frac{4\sqrt{2}}{7}$.

b) Ta có: (sin a + cos a)² = ${\left(\frac{1}{2}\right)}^2$$\iff {\sin }^{2}a+{\cos }^{2}a+2\sin a\cos a=\frac{1}{4}$

$\iff 1+\sin 2a=\frac{1}{4}\iff \sin 2a=-\frac{3}{4}$.

Vì $\frac{\pi }{2}<a<\frac{3\pi }{4}$ nên $\pi <2a<\frac{3\pi }{2}$, do đó cos 2a < 0. Mặt khác từ sin² (2a) + cos² (2a) = 1

Suy ra $\cos 2a=-\sqrt{1-{\sin }^2\left(2a\right)}=-\sqrt{1-{\left(-\frac{3}{4}\right)}^2}=-\frac{\sqrt{7}}{4}$.

Do đó, $\tan 2a=\frac{\sin 2a}{\cos 2a}=\frac{-\frac{3}{4}}{-\frac{\sqrt{7}}{4}}=\frac{3}{\sqrt{7}}=\frac{3\sqrt{7}}{7}$.

Bài 1.10 trang 21 Toán 11 Tập 1: Tính giá trị của các biểu thức sau:

a) $A=\frac{\sin \frac{\pi }{15}\cos \frac{\pi }{10}+\sin \frac{\pi }{10}\cos \frac{\pi }{15}}{\cos \frac{2\pi }{15}\cos \frac{\pi }{5}-\sin \frac{2\pi }{15}\sin \frac{\pi }{5}}$;

b) $B=\sin \frac{\pi }{32}\cos \frac{\pi }{32}\cos \frac{\pi }{16}\cos \frac{\pi }{8}$.

Lời giải:

a) Ta có:

$A=\frac{\sin \frac{\pi }{15}\cos \frac{\pi }{10}+\sin \frac{\pi }{10}\cos \frac{\pi }{15}}{\cos \frac{2\pi }{15}\cos \frac{\pi }{5}-\sin \frac{2\pi }{15}\sin \frac{\pi }{5}}$$=\frac{\sin \frac{\pi }{15}\cos \frac{\pi }{10}+\cos \frac{\pi }{15}\sin \frac{\pi }{10}}{\cos \frac{2\pi }{15}\cos \frac{\pi }{5}-\sin \frac{2\pi }{15}\sin \frac{\pi }{5}}$

$=\frac{\sin \left(\frac{\pi }{15}+\frac{\pi }{10}\right)}{\cos \left(\frac{2\pi }{15}+\frac{\pi }{5}\right)}$$=\frac{\sin \frac{\pi }{6}}{\cos \frac{\pi }{3}}=\frac{\frac{1}{2}}{\frac{1}{2}}=1$.

b) Ta có:

$B=\sin \frac{\pi }{32}\cos \frac{\pi }{32}\cos \frac{\pi }{16}\cos \frac{\pi }{8}$$=\left(\frac{1}{2}.2\sin \frac{\pi }{32}\cos \frac{\pi }{32}\right)\cos \frac{\pi }{16}\cos \frac{\pi }{8}$

$=\frac{1}{2}\sin \left(2.\frac{\pi }{32}\right)\cos \frac{\pi }{16}\cos \frac{\pi }{8}$$=\frac{1}{2}\sin \frac{\pi }{16}\cos \frac{\pi }{16}\cos \frac{\pi }{8}$

$=\frac{1}{4}.2\sin \frac{\pi }{16}\cos \frac{\pi }{16}\cos \frac{\pi }{8}$$=\frac{1}{4}\sin \frac{\pi }{8}\cos \frac{\pi }{8}=\frac{1}{8}.2\sin \frac{\pi }{8}\cos \frac{\pi }{8}$

$=\frac{1}{8}\sin \frac{\pi }{4}=\frac{1}{8}.\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{16}$.

Bài 1.11 trang 21 Toán 11 Tập 1: Chứng minh đẳng thức sau:

sin(a + b) sin(a – b) = sin² a – sin² b = cos² b – cos² a.

Lời giải:

Ta có: sin(a + b) sin(a – b) = $\frac{1}{2}$[cos(a + b – a + b) – cos(a + b + a – b)]

= $\frac{1}{2}$[cos 2b – cos 2a] = $\frac{1}{2}$[(2cos² b – 1) – (2cos² a – 1)] = cos² b – cos² a.

Vậy sin(a + b) sin(a – b) = cos² b – cos² a (1).

Lại có, cos 2b – cos 2a = (1 – 2sin² b) – (1 – 2sin² a) = 2(sin² a – sin² b)

Do đó, $\frac{1}{2}$[cos 2b – cos 2a] = $\frac{1}{2}$. 2(sin² a – sin² b) = sin² a – sin² b.

Vậy sin(a + b) sin(a – b) = sin² a – sin² b (2).

Từ (1) và (2), suy ra sin(a + b) sin(a – b) = sin² a – sin² b = cos² b – cos² a (đpcm).

Bài 1.12 trang 21 Toán 11 Tập 1: Cho tam giác ABC có $\widehat{B}=75°$; $\widehat{C}=45°$ và a = BC = 12 cm.

a) Sử dụng công thức $S=\frac{1}{2}ab\sin C$ và định lí sin, hãy chứng minh diện tích của tam giác ABC cho bởi công thức

$S=\frac{a^2\sin B\sin C}{2\sin A}$.

b) Sử dụng kết quả ở câu a và công thức biến đổi tích thành tổng, hãy tính diện tích S của tam giác ABC.

Lời giải:

a) Định lí sin trong tam giác ABC với BC = a, AC = b và AB = c là: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

Từ đó suy ra $b=\frac{a\sin B}{\sin A}$.

Diện tích tam giác ABC là $S=\frac{1}{2}ab\sin C$$=\frac{1}{2}a.\frac{a\sin B}{\sin A}.\sin C=\frac{a^2\sin B\sin C}{2\sin A}$.

Vậy $S=\frac{a^2\sin B\sin C}{2\sin A}$ (đpcm).

b) Ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong tam giác ABC).

$\Rightarrow \widehat{A}=180°-\left(\widehat{B}+\widehat{C}\right)=180°-\left(75°+45°\right)=60°$.

Ta có: $S=\frac{a^2\sin B\sin C}{2\sin A}=\frac{{12}^2\sin 75°\sin 45°}{2\sin 60°}$

$=\frac{144.\frac{1}{2}\left[\cos \left(75°-45°\right)-\cos \left(75°+45°\right)\right]}{2.\frac{\sqrt{3}}{2}}$

$=\frac{72\left(\cos 30°-\cos 120°\right)}{\sqrt{3}}$$=\frac{72\left(\frac{\sqrt{3}}{2}-\left(-\frac{1}{2}\right)\right)}{\sqrt{3}}=36+12\sqrt{3}$.

Vậy diện tích của tam giác ABC là $S=36+12\sqrt{3}$ (đvdt).

Bài 1.13 trang 21 Toán 11 Tập 1: Trong Vật lí, phương trình tổng quát của một vật dao động điều hòa cho bởi công thức x(t) = Acos(ωt + φ), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là biên độ dao động (A > 0) và φ ∈ [–π; π] là pha ban đầu của dao động.

Xét hai dao động điều hòa có phương trình:

$x_1\left(t\right)=2\cos \left(\frac{\pi }{3}t+\frac{\pi }{6}\right)$ (cm),

$x_2\left(t\right)=2\cos \left(\frac{\pi }{3}t-\frac{\pi }{3}\right)$ (cm).

Tìm dao động tổng hợp x(t) = x₁(t) + x₂(t) và sử dụng công thức biến đổi tổng thành tích để tìm biên độ và pha ban đầu của dao động tổng hợp này.

Lời giải:

Dao động tổng hợp x(t) = x₁(t) + x₂(t)

Suy ra x(t) = $2\cos \left(\frac{\pi }{3}t+\frac{\pi }{6}\right)+2\cos \left(\frac{\pi }{3}t-\frac{\pi }{3}\right)$ (cm).

Ta có: $2\cos \left(\frac{\pi }{3}t+\frac{\pi }{6}\right)+2\cos \left(\frac{\pi }{3}t-\frac{\pi }{3}\right)$

$=2\left[\cos \left(\frac{\pi }{3}t+\frac{\pi }{6}\right)+\cos \left(\frac{\pi }{3}t-\frac{\pi }{3}\right)\right]$

$=2.2\cos \frac{\left(\frac{\pi }{3}t+\frac{\pi }{6}\right)+\left(\frac{\pi }{3}t-\frac{\pi }{3}\right)}{2}\cos \frac{\left(\frac{\pi }{3}t+\frac{\pi }{6}\right)-\left(\frac{\pi }{3}t-\frac{\pi }{3}\right)}{2}$

$=4\cos \left(\frac{\pi }{6}t-\frac{\pi }{12}\right)\cos \frac{\pi }{4}$$=4\cos \left(\frac{\pi }{6}t-\frac{\pi }{12}\right).\frac{\sqrt{2}}{2}=2\sqrt{2}\cos \left(\frac{\pi }{6}t-\frac{\pi }{12}\right)$.

Vậy dạo động tổng hợp có phương trình là $x\left(t\right)=2\sqrt{2}\cos \left(\frac{\pi }{6}t-\frac{\pi }{12}\right)$ với biên độ $A=2\sqrt{2}$ và pha ban đầu là $\phi =-\frac{\pi }{12}$.

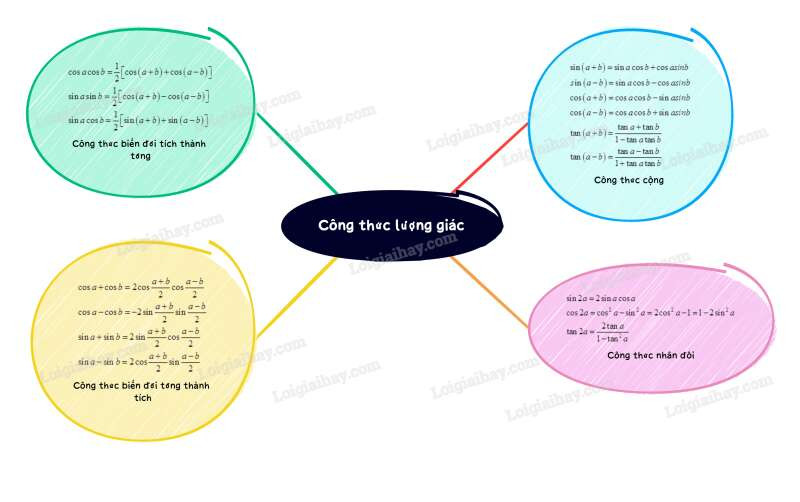
Lý thuyết Công thức lượng giác

1. Công thức cộng

$\begin{array}{l}\sin \left(a+b\right)=\sin a\cos b+\cos asinb\\ sin\left(a-b\right)=\sin a\cos b-\cos asinb\\ \cos \left(a+b\right)=\cos a\cos b-\sin asinb\\ \cos \left(a-b\right)=\cos a\cos b+\sin asinb\\ \tan \left(a+b\right)=\frac{\tan a+\tan b}{1-\tan a\tan b}\\ \tan \left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a\tan b}\end{array}$

2. Công thức nhân đôi

$\begin{array}{l}\sin 2a=2\sin a\cos a\\ \cos 2a={\cos }^{2}a-{\sin }^{2}a=2{\cos }^{2}a-1=1-2{\sin }^{2}a\\ \tan 2a=\frac{2\tan a}{1-{\tan }^{2}a}\end{array}$

Suy ra, công thức hạ bậc:

${\sin }^{2}a=\frac{1-\cos 2a}{2},{\cos }^{2}a=\frac{1+\cos 2a}{2}$

3. Công thức biến đổi tích thành tổng

$\begin{array}{l}\cos a\cos b=\frac{1}{2}\left[\cos \left(a+b\right)+\cos \left(a-b\right)\right]\\ \sin a\sin b=\frac{1}{2}\left[\cos \left(a-b\right)-\cos \left(a+b\right)\right]\\ \sin a\cos b=\frac{1}{2}\left[\sin \left(a+b\right)+\sin \left(a-b\right)\right]\end{array}$

4. Công thức biến đổi tổng thành tích

$\begin{array}{l}\cos a+\cos b=2\cos \frac{a+b}{2}\cos \frac{a-b}{2}\\ \cos a-\cos b=-2\sin \frac{a+b}{2}\sin \frac{a-b}{2}\\ \sin a+\sin b=2\sin \frac{a+b}{2}\cos \frac{a-b}{2}\\ \sin a-\sin b=2\cos \frac{a+b}{2}\sin \frac{a-b}{2}\end{array}$

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Bài 1: Giá trị lượng giác của góc lượng giác

Bài 2: Công thức lượng giác

Bài 3: Hàm số lượng giác

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1