Toán 11 Bài 15 (Kết nối tri thức): Giới hạn của dãy số
Với giải bài tập Toán lớp 11 Bài 15: Giới hạn của dãy số sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 Bài 15.
Giải Toán 11 Bài 15: Giới hạn của dãy số
Bài giảng Toán 11 Bài 15: Giới hạn của dãy số
1. Giới hạn hữu hạn của dãy số
HĐ1 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn là 0
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ un đến 0 nhỏ hơn 0,01?
Lời giải:
a) Năm số hạng đầu của dãy số (un) đã cho là ; ; ; ; .
Biểu diễn các số hạng này trên trục số, ta được:
b) Khoảng cách từ un đến 0 là 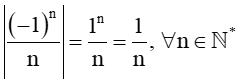
Ta có: .
Vậy bắt đầu từ số hạng thứ 101 của dãy thì khoảng cách từ un đến 0 nhỏ hơn 0,01.
Luyện tập 1 trang 105 Toán 11 Tập 1: Chứng minh rằng .
Lời giải:
Xét dãy số (un) có .
Ta có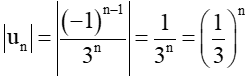
Do đó, .
HĐ2 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn hữu hạn
Cho dãy số (un) với . Xét dãy số (vn) xác định bởi vn = un – 1.
Lời giải:
Ta có: vn = un – 1 = .
Do đó, .
Luyện tập 2 trang 106 Toán 11 Tập 1: Cho dãy số (un) với . Chứng minh rằng .
Lời giải:
Ta có: khi n ⟶ +∞.
Do vây, .
Lời giải:
Một quả bóng cao su được thả từ độ cao 5 m xuống mặt sàn, sau lần chạm sàn đầu tiên, quả bỏng nảy lên một độ cao là u1 = .
Tiếp đó, bóng rơi từ độ cao u1 xuống mặt sàn và nảy lên độ cao là .
Tiếp đó, bóng rơi từ độ cao u2 xuống mặt sàn và nảy lên độ cao là và cứ tiếp tục như vậy.
Sau lần chạm sàn thứ n, quả bóng nảy lên độ cao là .
Ta có: , do đó, , suy ra điều phải chứng minh.
2. Định lí về giới hạn hữu hạn của dãy số
HĐ3 trang 106 Toán 11 Tập 1: Hình thành quy tắc tính giới hạn
Cho hai dãy số (un) và (vn) với .
Lời giải:
+) Ta có: .
Lại có khi n ⟶ +∞.
Do vậy, .
+) Ta có: khi n ⟶ +∞.
Do vậy, .
Và khi n ⟶ +∞.
Do vây, .
Khi đó, = 2 + 3 = 5 = .
Vậy = .
Luyện tập 3 trang 107 Toán 11 Tập 1: Tìm .
Lời giải:
Áp dụng các quy tắc tính giới hạn, ta được:
.
3. Tổng của cấp số nhân lùi vô hạn
HĐ4 trang 107 Toán 11 Tập 1: Làm quen với việc tính tổng vô hạn
a) Tính tổng Sn = u1 + u2 + ... + un.
Lời giải:
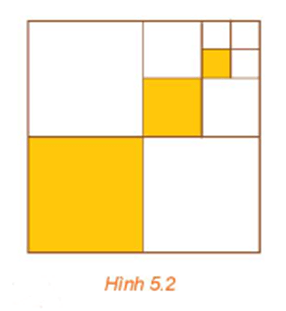
a) Ta có: u1 là độ dài cạnh của hình vuông được tô màu tạo từ việc chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau, do đó .
Cứ tiếp tục như thế, ta được: ,..., , ...
Do vậy, độ dài cạnh của các hình vuông được tô màu lập thành một cấp số nhân với số hạng đầu và công bội .
Do đó, tổng của n số hạng đầu là
Sn = u1 + u2 + ... + un = .
b) Ta có: S = = .
Luyện tập 4 trang 108 Toán 11 Tập 1: Tính tổng
Lời giải:
Đây là tổng của cấp số nhân lùi vô hạn với u1 = 2 và q = .
Do đó, .
Vận dụng 2 trang 108 Toán 11 Tập 1: (Giải thích nghịch lí Zeno)
c) Sai lầm trong lập luận của Zeno là ở đâu?
Lời giải:
Ta có: Achilles chạy với vận tốc 100 km/h, vận tốc của rùa là 1 km/h.
a) Để chạy hết quãng đường từ A1 đến A2 với A1A2 = a = 100 (km), Achilles phải mất thời gian (h). Với thời gian t1 này, rùa đã chạy được quãng đường A2A3 = 1 (km).
Để chạy hết quãng đường từ A2 đến A3 với A2A3 = 1 (km), Achilles phải mất thời gian (h). Với thời gian t2 này, rùa đã chạy được quãng đường A3A4 = (km).
Tiếp tục như vậy, để chạy hết quãng đường từ An đến An + 1 với AnAn + 1 = (km), Achilles phải mất thời gian (h). ...
b) Tổng thời gian cần thiết để Achilles chạy hết các quãng đường A1A2, A2A3, ..., AnAn + 1, ..., tức là thời gian cần thiết để Achilles đuổi kịp rùa là
(h).
Đó là tổng của một cấp số nhân lùi vô hạn với u1 = 1, công bội , nên ta có
(h).
Như vậy, Achilles đuổi kịp rùa sau giờ.
c) Nghịch lý Zeno chỉ đúng với điều kiện là tổng thời gian Achilles chạy hết các quãng đường để đuổi kịp rùa phải là vô hạn, còn nếu nó hữu hạn thì đó chính là khoảng thời gian mà anh bắt kịp được rùa.
4. Tổng của cấp số nhân lùi vô hạn
HĐ5 trang 108 Toán 11 Tập 1: Nhận biết giới hạn vô cực
a) Dự đoán công thức tính số vi khuẩn un sau chu kì thứ n.
b) Sau bao lâu, số lượng vi khuẩn sẽ vượt con số 10 000?
Lời giải:
a) Ta có số lượng ban đầu của vi khuẩn là u0 = 50.
Sau chu kì thứ nhất, số lượng vi khuẩn là u1 = 2u0 = 2 . 50.
Sau chu kì thứ hai, số lượng vi khuẩn là u2 = 2u1 = 2 . 2 . 50 = 22 . 50.
Cứ tiếp tục như vậy, ta dự đoán được sau chu kì thứ n, số lượng vi khuẩn là un = 2n . 50.
b) Giả sử sau chu kì thứ k, số lượng vi khuẩn sẽ vượt con số 10 000.
Khi đó ta có uk = 2k . 50 > 10 000 ⇔ 2k > 200.
Luyện tập 5 trang 109 Toán 11 Tập 1: Tính .
Lời giải:
Ta có: . Hơn nữa và .
Do đó, .
Bài tập
Bài 5.1 trang 109 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) .
b)
.
Bài 5.2 trang 109 Toán 11 Tập 1: Cho hai dãy số không âm (un) và (vn) với và . Tìm các giới hạn sau:
Lời giải:
a) Ta có: , do đó, .
Và nên .
Vậy .
b) Ta có: và , do đó, .
Và nên .
Vì un ≥ 0, vn ≥ 0 với mọi n nên un + 2vn ≥ 0 với mọi n và .
Do đó, .
Bài 5.3 trang 109 Toán 11 Tập 1: Tìm giới hạn của các dãy số cho bởi:
Lời giải:
a)
Chia cả tử và mẫu của un cho n2, ta được .
Vì , và với mọi n nên
.
b)
Ta có:
Vì và .
Nên
Vậy .
Bài 5.4 trang 109 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số:
Lời giải:
a) Ta có: 1,(12) = 1,121212... = 1 + 0,12 + 0,0012 + 0,000012 + ...
= 1 + 12 . 10-2 + 12 . 10-4 + 12 . 10-6 + ...
= 1 + 12 . (10-2 + 10-4 + 10-6 + ...)
Do 10-2 + 10-4 + 10-6 + ... là tổng của cấp số nhân lùi vô hạn với u1 = 10-2 và q = 10-2 nên
10-2 + 10-4 + 10-6 + ... = .
Vậy 1,(12) = .
b) Ta có: 3,(102) = 3,102102102... = 3 + 0,102 + 0,000102 + 0,000000102 + ...
= 3 + 102 . 10-3 + 102 . 10-6 + 102 . 10-9 + ...
= 3 + 102 . (10-3 + 10-6 + 10-9 + ...)
Do 10-3 + 10-6 + 10-9 + ... là tổng của cấp số nhân lùi vô hạn với u1 = 10-3 và q = 10-3 nên
10-3 + 10-6 + 10-9 + ... = .
Vậy 3,(102) = 3 + .
Lời giải:
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày đầu tiên là 150 mg.
Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%.
Do đó, lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ hai là
150 + 150 . 5% = 150(1 + 0,05).
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ ba là
150 + 150(1 + 0,05) . 5% = 150 + 150(0,05 + 0,052) = 150(1 + 0,05 + 0,052)
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ tư là
150 + 150(1 + 0,05 + 0,052) . 5% = 150(1 + 0,05 + 0,052 + 0,053)
Lượng thuốc trong cơ thể bệnh nhân sau khi uống viên thuốc của ngày thứ năm là
150 + 150(1 + 0,05 + 0,052 + 0,053) . 5% = 150(1 + 0,05 + 0,052 + 0,053 + 0,054)
= 157,8946875 (mg).
Cứ tiếp tục như vậy, ta ước tính lượng thuốc trong cơ thể bệnh nhân nếu bệnh nhân sử dụng thuốc trong một thời gian dài là
S = 150(1 + 0,05 + 0,052 + 0,053 + 0,054 + ...)
Lại có 1 + 0,05 + 0,052 + 0,053 + 0,054 + ... là tổng của cấp số nhân lùi vô hạn với số hạng đầu u1 = 1 và công bội q = 0,05.
Do đó, 1 + 0,05 + 0,052 + 0,053 + 0,054 + ... = .
Suy ra S = .
Lời giải:
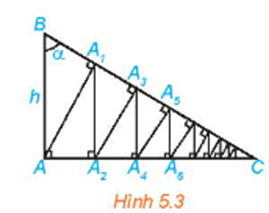
Tam giác AA1B vuông tại A1 có AB = h và .
Do đó, AA1 = AB sinB = h sin α.
Ta có: và , suy ra .
Tam giác AA1A2 vuông tại A2 nên A1A2 = AA1 sin = h sin α . sin α = h sin2 α.
Vì AB ⊥ AC và A1A2 ⊥ AC nên AB // A1A2, suy ra (2 góc đồng vị).
Tam giác A1A2A3 vuông tại A3 nên A2A3 = A1A2 . sin = h sin2 α . sin α = h sin3 α.
Vì AA1 ⊥ BC và A2A3 ⊥ BC nên AA1 // A2A3, suy ra .
Tam giác A2A3A4 vuông tại A4 nên A3A4 = A2A3 . sin = h sin3 α . sin α = h sin4 α.
Cứ tiếp tục như vậy, ta xác định được An – 1An = h sinn α.
Ta có: AA1A2A3... = AA1 + A1A2 + A2A3 + ... + An – 1An + ...
= h sin α + h sin2 α + h sin3 α + ... + h sinn α + ...
Vì góc B là góc nhọn nên sin B = sin α < 1, do đó |sin α| < 1.
Khi đó, độ dài của đường gấp khúc vô hạn AA1A2A3... là tổng của cấp số nhân lùi vô hạn với số hạng đầu u1 = h sin α và công bội q = sin α.
Do đó, AA1A2A3... = .
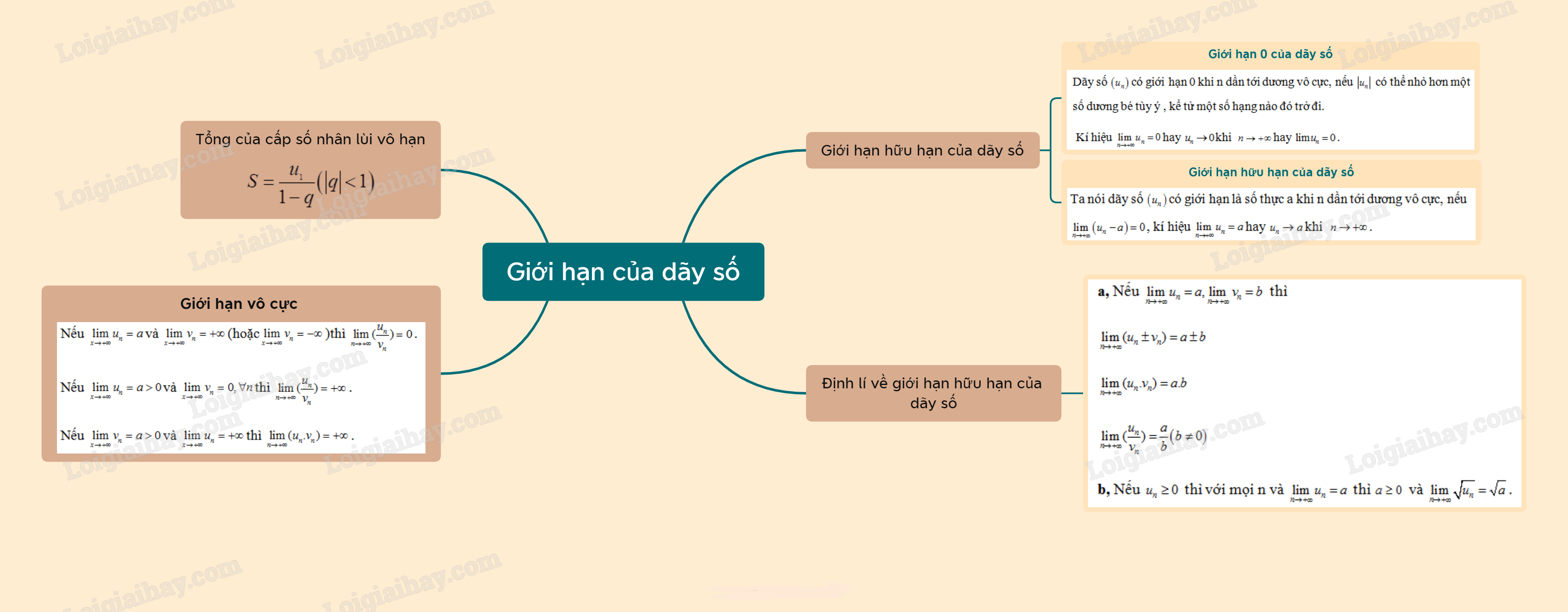
Lý thuyết Giới hạn của dãy số
1. Giới hạn hữu hạn của dãy số
Ta nói dãy số có giới hạn 0 khi n dần tới dương vô cực, nếu có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi, kí hiệu hay khi .
Ta nói dãy số có giới hạn là số thực a khi n dần tới dương vô cực, nếu , kí hiệu hay khi .
* Chú ý: Nếu (c là hằng số) thì
2. Định lí về giới hạn hữu hạn của dãy số
a, Nếu thì
b, Nếu thì với mọi n và thì và .
3. Tổng của cấp số nhân lùi vô hạn
4. Giới hạn vô cực của dãy số
Dãy số được gọi là có giới hạn khi nếu có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu hay khi .
Dãy số được gọi là có giới hạn khi nếu , kí hiệu hay khi .
*Quy tắc:
Nếu và (hoặc) thì .
Nếu và thì .
Nếu và thì .
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức