Toán 11 Bài 4 (Kết nối tri thức): Phương trình lượng giác cơ bản

Giải Toán 11 Bài 4: Phương trình lượng giác cơ bản

Bài giảng Toán 11 Bài 4: Phương trình lượng giác cơ bản

Giải Toán 11 trang 31 Tập 1

Mở đầu trang 31 Toán 11 Tập 1: Một quả đạn pháo được bán ra khỏi nòng pháo với vận tốc ban đầu có độ lớn v0 không đổi. Tìm góc bắn α để quả đạn pháo bay xa nhất, bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất.

Lời giải:

Sau bài học này ta sẽ giải quyết được bài toán trên như sau:

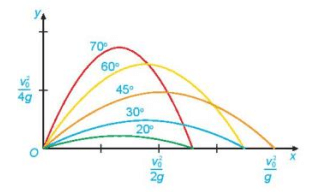
Chọn hệ trục tọa độ có gốc tọa độ đặt tại vị trí khẩu pháo, trục Ox theo hướng khẩu pháo như hình dưới đây.

Khi đó theo Vật lí, ta biết rằng quỹ đạo của quả đạn pháo có dạng đường parabol có phương trình $y=\frac{-g}{2v_0^2{\cos }^2\alpha }{x}^2+x\tan \alpha$ (với g là gia tốc trọng trường).

Cho y = 0 ta được $\frac{-g}{2v_0^2{\cos }^2\alpha }{x}^2+x\tan \alpha =0$, suy ra x = 0 hoặc $x=\frac{v_0^2\sin 2\alpha }{g}$.

Quả đạn tiếp đất khi $x=\frac{v_0^2\sin 2\alpha }{g}$.

Ta có $x=\frac{v_0^2\sin 2\alpha }{g}\le \frac{v_0^2}{g}$ , dấu bằng xảy ra khi sin 2α = 1.

Giải phương trình sin 2α = 1, ta được α = $\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$.

Do $0\le \alpha \le \frac{\pi }{2}$ nên $\alpha =\frac{\pi }{4}$ hay α = 45°.

Vậy quả đạn pháo sẽ bay xa nhất khi góc bắn bằng 45°.

HĐ1 trang 31 Toán 11 Tập 1: Nhận biết khái niệm hai phương trình tương đương

Cho hai phương trình 2x – 4 = 0 và (x – 2)(x² + 1) = 0.

Tìm và so sánh tập nghiệm của hai phương trình trên.

Lời giải:

+) Ta có: 2x – 4 = 0, suy ra x = 2.

Vậy tập nghiệm của phương trình 2x – 4 = 0 là S₁ = {2}.

+) Ta có: (x – 2)(x² + 1) = 0

Vì x² ≥ 0 với mọi x ∈ ℝ nên x² + 1 > 0 với mọi x ∈ ℝ.

Do đó, (x – 2)(x² + 1) = 0 khi x – 2 = 0 hay x = 2.

Vậy tập nghiệm của phương trình (x – 2)(x² + 1) = 0 là S₂ = {2}.

+) Nhận thấy S₁ = S₂ = {2}. Vậy hai phương trình đã cho có cùng tập nghiệm.

Giải Toán 11 trang 32 Tập 1

Luyện tập 1 trang 32 Toán 11 Tập 1: Xét sự tương đương của hai phương trình sau:

$\frac{x-1}{x+1}=0$ và x² – 1 = 0.

Lời giải:

+) Ta có: $\frac{x-1}{x+1}=0$, điều kiện x ≠ – 1.

Khi đó, $\frac{x-1}{x+1}=0$ khi x – 1 = 0 hay x = 1 (thỏa mãn).

Vậy tập nghiệm của phương trình $\frac{x-1}{x+1}=0$ là S₁ = {1}.

+) Phương trình x² – 1 = 0 được viết lại thành (x – 1)(x + 1) = 0, từ đó ta tìm được x = 1 hoặc x = – 1, do đó tập nghiệm của phương trình x² – 1 = 0 là S₂ = {– 1; 1}.

+) Nhận thấy S₁ ≠ S₂, vậy hai phương trình đã cho không tương đương.

HĐ2 trang 32 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình sin x = $\frac{1}{2}$

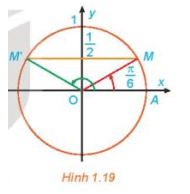
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).

b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a) Từ Hình 1.19, nhận thấy hai điểm M, M' lần lượt biểu diễn các góc $\frac{\pi }{6}$ và $\pi -\frac{\pi }{6}=\frac{5\pi }{6}$, lại có tung độ của điểm M và M' đều bằng $\frac{1}{2}$ nên theo định nghĩa giá trị lượng giác, ta có $\sin \frac{\pi }{6}=\frac{1}{2}$ và $\sin \frac{5\pi }{6}=\frac{1}{2}$.

Vậy trong nửa khoảng [0; 2π), phương trình $\sin x=\frac{1}{2}$ có hai nghiệm là $x=\frac{\pi }{6}$, $x=\frac{5\pi }{6}$.

b) Vì hàm số sin có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là $x=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$ và $x=\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

Giải Toán 11 trang 34 Tập 1

Luyện tập 2 trang 34 Toán 11 Tập 1: Giải các phương trình sau:

a) $\sin x=\frac{\sqrt{2}}{2}$;

b) sin 3x = – sin 5x.

Lời giải:

a) $\sin x=\frac{\sqrt{2}}{2}$

$\iff \sin x=\sin \frac{\pi }{4}$

$\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k2\pi \\ x=\pi -\frac{\pi }{4}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k2\pi \\ x=\frac{3\pi }{4}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình $\sin x=\frac{\sqrt{2}}{2}$ có các nghiệm là $x=\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}$ và $x=\frac{3\pi }{4}+k2\pi$, $k\in \mathbb{Z}$.

b) sin 3x = – sin 5x

⇔ sin 3x = sin (– 5x)

$\iff \left[\begin{array}{l}3x=-5x+k2\pi \\ 3x=\pi -\left(-5x\right)+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}3x=-5x+k2\pi \\ 3x=\pi +5x+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}8x=k2\pi \\ -2x=\pi +k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=k\frac{\pi }{4}\\ x=-\frac{\pi }{2}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình đã cho có các nghiệm là $x=k\frac{\pi }{4},k\in \mathbb{Z}$ và $x=-\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$.

HĐ3 trang 34 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cos x = $-\frac{1}{2}$

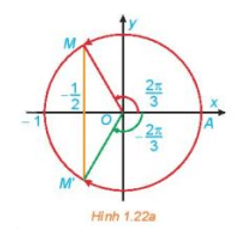
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng [– π; π).

b) Dựa vào tính tuần hoàn của hàm số côsin, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a) Từ Hình 1.22a, nhận thấy hai điểm M, M' lần lượt biểu diễn các góc $\frac{2\pi }{3}$ và $-\frac{2\pi }{3}$, lại có hoành độ của điểm M và M' đều bằng $-\frac{1}{2}$ nên theo định nghĩa giá trị lượng giác, ta có $\cos \frac{2\pi }{3}=-\frac{1}{2}$ và $\cos \left(-\frac{2\pi }{3}\right)=-\frac{1}{2}$.

Vậy trong nửa khoảng [– π; π), phương trình $\cos x=-\frac{1}{2}$ có hai nghiệm là $x=\frac{2\pi }{3}$, $x=-\frac{2\pi }{3}$.

b) Vì hàm số cos có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là $x=\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$ và $x=-\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

Giải Toán 11 trang 35 Tập 1

Luyện tập 3 trang 35 Toán 11 Tập 1: Giải các phương trình sau:

a) 2cos x = $-\sqrt{2}$ ;

b) cos 3x – sin 5x = 0.

Lời giải:

a) 2cos x = $-\sqrt{2}$

$\iff \cos x=-\frac{\sqrt{2}}{2}$

$\iff \cos x=\cos \frac{3\pi }{4}$

$\iff \left[\begin{array}{l}x=\frac{3\pi }{4}+k2\pi \\ x=-\frac{3\pi }{4}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình đã cho có các nghiệm là $x=\frac{3\pi }{4}+k2\pi ,k\in \mathbb{Z}$ và $x=-\frac{3\pi }{4}+k2\pi ,k\in \mathbb{Z}$.

b) cos 3x – sin 5x = 0

⇔ cos 3x = sin 5x

$\iff \cos 3x=\cos \left(\frac{\pi }{2}-5x\right)$

$\iff \left[\begin{array}{l}3x=\frac{\pi }{2}-5x+k2\pi \\ 3x=-\left(\frac{\pi }{2}-5x\right)+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}8x=\frac{\pi }{2}+k2\pi \\ 2x=\frac{\pi }{2}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=\frac{\pi }{16}+k\frac{\pi }{4}\\ x=\frac{\pi }{4}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình đã cho có các nghiệm là $x=\frac{\pi }{16}+k\frac{\pi }{4},k\in \mathbb{Z}$ và $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$

Vận dụng trang 35 Toán 11 Tập 1: Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là α (0° ≤ α ≤ 360°) thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bởi công thức

$F=\frac{1}{2}\left(1-\cos \alpha \right)$.

(Theo trang usno.navy.mil).

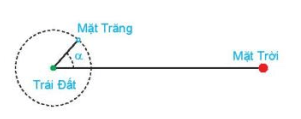
Xác định góc α tương ứng với các pha sau của Mặt Trăng:

a) F = 0 (trăng mới);

b) F = 0,25 (trăng lưỡi liềm);

c) F = 0,5 (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng);

d) F = 1 (trăng tròn).

Lời giải:

a) Với F = 0, ta có $\frac{1}{2}\left(1-\cos \alpha \right)=0$ ⇔ cos α = 1 ⇔ α = k2π, k ∈ ℤ.

b) Với F = 0,25, ta có $\frac{1}{2}\left(1-\cos \alpha \right)=\mathrm{0,25}$ $\iff \cos \alpha =\frac{1}{2}$

$\iff \cos \alpha =\cos \frac{\pi }{3}$$\iff \left[\begin{array}{l}\alpha =\frac{\pi }{3}+k2\pi \\ \alpha =-\frac{\pi }{3}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$.

c) Với F = 0,5, ta có $\frac{1}{2}\left(1-\cos \alpha \right)=\mathrm{0,5}$ ⇔ cos α = 0 ⇔ α = $\frac{\pi }{2}$ + kπ, k ∈ ℤ.

d) Với F = 1, ta có $\frac{1}{2}\left(1-\cos \alpha \right)=1$ ⇔ cos α = – 1 ⇔ α = π + k2π, k ∈ ℤ.

Giải Toán 11 trang 36 Tập 1

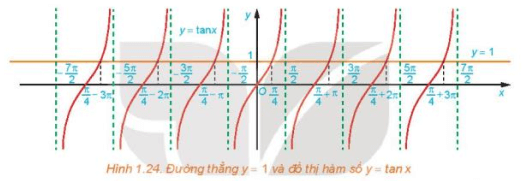
HĐ4 trang 36 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình tan x = 1

a) Quan sát Hình 1.24, hãy cho biết đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại mấy điểm trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$?

b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a) Quan sát Hình 1.24, ta thấy trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ , đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại 1 điểm, điểm này có hoành độ $x=\frac{\pi }{4}$ .

b) Từ câu a, ta suy ra phương trình tan x = 1 có nghiệm là $x=\frac{\pi }{4}$ trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ .

Do hàm số tang có chu kì là π, nên công thức nghiệm của phương trình tan x = 1 là $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$ .

Luyện tập 4 trang 36 Toán 11 Tập 1: Giải các phương trình sau:

a) $\sqrt{3}\tan 2x=-1$ ;

b) tan 3x + tan 5x = 0.

Lời giải:

a) $\sqrt{3}\tan 2x=-1$

$\iff \tan 2x=-\frac{1}{\sqrt{3}}$

$\iff \tan 2x=\tan \left(-\frac{\pi }{6}\right)$

$\iff 2x=-\frac{\pi }{6}+k\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{\pi }{12}+k\frac{\pi }{2},k\in \mathbb{Z}$

Vậy phương trình đã cho có nghiệm là $x=-\frac{\pi }{12}+k\frac{\pi }{2},k\in \mathbb{Z}$ .

b) tan 3x + tan 5x = 0

⇔ tan 3x = – tan 5x

⇔ tan 3x = tan (– 5x)

⇔ 3x = – 5x + kπ, k ∈ ℤ

⇔ 8x = kπ, k ∈ ℤ

⇔ x = $k\frac{\pi }{8},k\in \mathbb{Z}$

Vậy phương trình đã cho có nghiệm là x = $k\frac{\pi }{8},k\in \mathbb{Z}$ .

Giải Toán 11 trang 37 Tập 1

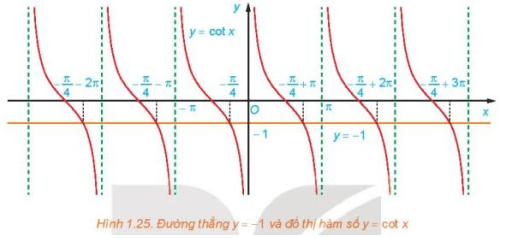
HĐ5 trang 37 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cot x = – 1

a) Quan sát Hình 1.25, hãy cho biết đường thẳng y = – 1 cắt đồ thị hàm số y = cot x tại mấy điểm trên khoảng (0; π)?

b) Dựa vào tính tuần hoàn của hàm côtang, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a) Quan sát Hình 1.25, ta thấy trên khoảng (0; π), đường thẳng y = – 1 cắt đồ thị hàm số y = cot x tại 1 điểm, điểm này có hoành độ $x=-\frac{\pi }{4}+\pi =\frac{3\pi }{4}$.

b) Từ câu a, ta suy ra phương trình cot x = – 1 có nghiệm là $x=\frac{3\pi }{4}$ trên khoảng (0; π).

Do hàm số côtang có chu kì là π, nên công thức nghiệm của phương trình cot x = – 1 là $x=\frac{3\pi }{4}+k\pi ,k\in \mathbb{Z}$.

Luyện tập 5 trang 37 Toán 11 Tập 1: Giải các phương trình sau:

a) cot x = 1;

b) $\sqrt{3}\cot x+1=0$.

Lời giải:

a) cot x = 1

$\iff \cot x=\cot \frac{\pi }{4}$

$\iff x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$

Vậy phương trình đã cho có nghiệm là $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$ .

b) $\sqrt{3}\cot x+1=0$

$\iff \cot x=-\frac{1}{\sqrt{3}}$

$\iff \cot x=\cot \left(-\frac{\pi }{3}\right)$

$\iff x=-\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}$

Vậy phương trình đã cho có nghiệm là $x=-\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}$.

Giải Toán 11 trang 38 Tập 1

Luyện tập 6 trang 38 Toán 11 Tập 1: Sử dụng máy tính cầm tay, tìm số đo độ và rađian của góc α, biết:

a) cos α = – 0,75;

b) tan α = 2,46;

c) cot α = – 6,18.

Lời giải:

a) cos α = – 0,75

+ Để tìm số đo độ của góc α, ta bấm phím như sau:

$\boxed{SHIFT}\boxed{MODE}\boxed{3}\boxed{SHIFT}\boxed{\cos }\boxed{-}\boxed{0}\boxed{.}\boxed{7}\boxed{5}\boxed{=}\boxed{°"\text{'}}$

Màn hình hiện kết quả là: 138°35'25,36''.

Vậy α ≈ 138°35'26".

+ Để tìm số đo rađian của góc α, ta bấm phím như sau:

$\boxed{SHIFT}\boxed{MODE}\boxed{4}\boxed{SHIFT}\boxed{\cos }\boxed{-}\boxed{0}\boxed{.}\boxed{7}\boxed{5}\boxed{=}$

Màn hình hiện kết quả là: 2,418858406.

Vậy α ≈ 2,41886 rad.

b) tan α = 2,46

+ Để tìm số đo độ của góc α, ta bấm phím như sau:

$\boxed{SHIFT}\boxed{MODE}\boxed{3}\boxed{SHIFT}\boxed{\tan }\boxed{2}\boxed{.}\boxed{4}\boxed{6}\boxed{=}\boxed{°"\text{'}}$

Màn hình hiện kết quả là: 67°52'41,01".

Vậy α ≈ 67°52'41".

+ Để tìm số đo rađian của góc α, ta bấm phím như sau:

$\boxed{SHIFT}\boxed{MODE}\boxed{4}\boxed{SHIFT}\boxed{\tan }\boxed{2}\boxed{.}\boxed{4}\boxed{6}\boxed{=}$

Màn hình hiện kết quả là: 1,184695602.

Vậy α ≈ 1,1847 rad.

c) cot α = – 6,18

+ Để tìm số đo độ của góc α, ta bấm phím như sau:

Màn hình hiện kết quả là: – 9°11'29,38".

Vậy α ≈ – 9°11'30".

+ Để tìm số đo rađian của góc α, ta bấm phím như sau:

Màn hình hiện kết quả là: – 0,1604218219.

Vậy α ≈ – 0,16042 rad.

Giải Toán 11 trang 39 Tập 1

Bài tập

Bài 1.19 trang 39 Toán 11 Tập 1: Giải các phương trình sau:

a) $\sin x=\frac{\sqrt{3}}{2}$ ;

b) $2\cos x=-\sqrt{2}$ ;

c) $\sqrt{3}\tan \left(\frac{x}{2}+15°\right)=1$ ;

d) $\cot \left(2x-1\right)=\cot \frac{\pi }{5}$ .

Lời giải:

a) $\sin x=\frac{\sqrt{3}}{2}$

$\iff \sin x=\sin \frac{\pi }{3}$

$\iff \left[\begin{array}{l}x=\frac{\pi }{3}+k2\pi \\ x=\pi -\frac{\pi }{3}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=\frac{\pi }{3}+k2\pi \\ x=\frac{2\pi }{3}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình đã cho có các nghiệm là $x=\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$ và $x=\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$ .

b) $2\cos x=-\sqrt{2}$

$\iff \cos x=-\frac{\sqrt{2}}{2}$

$\iff \cos x=\cos \frac{3\pi }{4}$

$\iff \left[\begin{array}{l}x=\frac{3\pi }{4}+k2\pi \\ x=-\frac{3\pi }{4}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình đã cho có các nghiệm là $x=\frac{3\pi }{4}+k2\pi ,k\in \mathbb{Z}$ và $x=-\frac{3\pi }{4}+k2\pi ,k\in \mathbb{Z}$ .

c) $\sqrt{3}\tan \left(\frac{x}{2}+15°\right)=1$

$\iff \tan \left(\frac{x}{2}+15°\right)=\frac{1}{\sqrt{3}}$

$\iff \tan \left(\frac{x}{2}+15°\right)=\tan 30°$

$\iff \frac{x}{2}+15°=30°+k180°,k\in \mathbb{Z}$

$\iff x=30°+k360°,k\in \mathbb{Z}$

Vậy phương trình đã cho có nghiệm là x = 30° + k360°, k ∈ ℤ.

d) $\cot \left(2x-1\right)=\cot \frac{\pi }{5}$

$\iff 2x-1=\frac{\pi }{5}+k\pi ,k\in \mathbb{Z}$

$\iff x=\frac{\pi }{10}+\frac{1}{2}+k\frac{\pi }{2},k\in \mathbb{Z}$

Vậy phương trình đã cho có nghiệm là $x=\frac{\pi }{10}+\frac{1}{2}+k\frac{\pi }{2},k\in \mathbb{Z}$ .

Bài 1.20 trang 39 Toán 11 Tập 1: Giải các phương trình sau:

a) sin 2x + cos 4x = 0;

b) cos 3x = – cos 7x.

Lời giải:

a) sin 2x + cos 4x = 0

⇔ cos 4x = – sin 2x

⇔ cos 4x = sin(– 2x)

⇔ cos 4x = cos$\left(\frac{\pi }{2}-\left(-2x\right)\right)$

⇔ cos 4x = cos$\left(\frac{\pi }{2}+2x\right)$

$\iff \left[\begin{array}{l}4x=\frac{\pi }{2}+2x+k2\pi \\ 4x=-\left(\frac{\pi }{2}+2x\right)+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=-\frac{\pi }{12}+k\frac{\pi }{3}\end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình đã cho có các nghiệm là $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$ và $x=-\frac{\pi }{12}+k\frac{\pi }{3},k\in \mathbb{Z}$ .

b) cos 3x = – cos 7x

⇔ cos 3x = cos(π + 7x)

$\iff \left[\begin{array}{l}3x=\pi +7x+k2\pi \\ 3x=-\left(\pi +7x\right)+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=-\frac{\pi }{4}+k\frac{\pi }{2}\\ x=-\frac{\pi }{10}+k\frac{\pi }{5}\end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình đã cho có các nghiệm là $x=-\frac{\pi }{4}+k\frac{\pi }{2},k\in \mathbb{Z}$ và $x=-\frac{\pi }{10}+k\frac{\pi }{5},k\in \mathbb{Z}$.

Bài 1.21 trang 39 Toán 11 Tập 1: Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu v₀ = 500 m/s hợp với phương ngang một góc α. Trong Vật lí, ta biết rằng, nếu bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất thì quỹ đạo của quả đạn tuân theo phương trình $y=\frac{-g}{2v_0^2{\cos }^2\alpha }{x}^2+x\tan \alpha$, ở đó g = 9,8 m/s² là gia tốc trọng trường.

a) Tính theo góc bắn α tầm xa mà quả đạn đạt tới (tức là khoảng cách từ vị trí bắn đến điểm quả đạn chạm đất).

b) Tìm góc bắn α để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m.

c) Tìm góc bắn α để quả đạn đạt độ cao lớn nhất.

Lời giải:

Vì v₀ = 500 m/s, g = 9,8 m/s² nên ta có phương trình quỹ đạo của quả đạn là

$y=\frac{-\mathrm{9,8}}{{2.500}^2.{\cos }^2\alpha }{x}^2+x\tan \alpha$ hay $y=\frac{-49}{2500000{\cos }^2\alpha }{x}^2+x\tan \alpha$ .

a) Quả đạn chạm đất khi y = 0, khi đó $\frac{-49}{2500000{\cos }^2\alpha }{x}^2+x\tan \alpha =0$

$\iff x\left(\frac{-49}{2500000{\cos }^2\alpha }x+\tan \alpha \right)=0$

$\iff \left[\begin{array}{l}x=0\\ x=\frac{2500000{\cos }^2\alpha .\tan \alpha }{49}\end{array}\right.$

$\iff \left[\begin{array}{l}x=0\\ x=\frac{2500000\cos \alpha .\sin \alpha }{49}\end{array}\right.$

$\iff \left[\begin{array}{l}x=0\\ x=\frac{1250000\sin 2\alpha }{49}\end{array}\right.$

Loại x = 0 (đạn pháo chưa được bắn).

Vậy tầm xa mà quả đạn đạt tới là $x=\frac{1250000\sin 2\alpha }{49}$ (m).

b) Để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m thì x = 22 000 m.

Khi đó $\frac{1250000\sin 2\alpha }{49}=22000$ ⇔ sin 2α = $\frac{539}{625}$

Gọi $\beta \in \left[-\frac{\pi }{2};\frac{\pi }{2}\right]$ là góc thỏa mãn $\sin \beta =\frac{539}{625}$ . Khi đó ta có: sin 2α = sin β

$\iff \left[\begin{array}{l}2\alpha =\beta +k2\pi \\ 2\alpha =\pi -\beta +k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$$\iff \left[\begin{array}{l}\alpha =\frac{\beta }{2}+k\pi \\ \alpha =\frac{\pi }{2}-\frac{\beta }{2}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$.

c) Hàm số $y=\frac{-49}{2500000{\cos }^2\alpha }{x}^2+x\tan \alpha$ là một hàm số bậc hai có đồ thị là một parabol có tọa độ đỉnh I(x_I; y_I) là

$\left\{\begin{array}{l}{x}_I=-\frac{b}{2a}=-\frac{\tan \alpha }{2.\frac{-49}{2500000{\cos }^2\alpha }}=\frac{1250000\cos \alpha \sin \alpha }{49}\\ y_I=f\left(x_I\right)=\frac{-49}{2500000{\cos }^2\alpha }{\left(\frac{1250000\cos \alpha \sin \alpha }{49}\right)}^2+\frac{1250000\cos \alpha \sin \alpha }{49}\tan \alpha \end{array}\right.$

Hay $\left\{\begin{array}{l}{x}_I=\frac{1250000\cos \alpha \sin \alpha }{49}\\ y_I=\frac{625000{\sin }^2\alpha }{49}\end{array}\right.$

Do đó, độ cao lớn nhất của quả đạn là $y_{\max }=\frac{625000{\sin }^2\alpha }{49}$.

Ta có $y_{\max }=\frac{625000{\sin }^2\alpha }{49}\le \frac{625000}{49}$ , dấu “=” xảy ra khi sin² α = 1 hay α = 90°.

Như vậy góc bắn α = 90° thì quả đan đạt độ cao lớn nhất.

Bài 1.22 trang 39 Toán 11 Tập 1: Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình

$x=2\cos \left(5t-\frac{\pi }{6}\right)$.

Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimét. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?

Lời giải:

Vị trí cân bằng của vật dao động điều hòa là vị trí vật đứng yên, khi đó x = 0, ta có

$2\cos \left(5t-\frac{\pi }{6}\right)=0$

$\iff \cos \left(5t-\frac{\pi }{6}\right)=0$

$\iff 5t-\frac{\pi }{6}=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$

$\iff t=\frac{2\pi }{15}+k\frac{\pi }{5},k\in \mathbb{Z}$

Trong khoảng thời gian từ 0 đến 6 giây, tức là 0 ≤ t ≤ 6 hay $0\le \frac{2\pi }{15}+k\frac{\pi }{5}\le 6$

$\iff -\frac{2}{3}\le k\le \frac{90-2\pi }{3\pi }$

Vì k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8}.

Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.

Lý thuyết Phương trình lượng giác cơ bản

1. Khái niệm phương trình tương đương

- Hai phương trình (cùng ẩn) được gọi là tương đương khi chúng có cùng tập nghiệm.

- Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết $f(x)=0\iff g(x)=0$

*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.

- Các phép biến đổi tương đương:

+ Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức.

+ Nhân hoặc chia 2 vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.

2. Phương trình $\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x}=m$

Phương trình sinx=m có nghiệm khi và chỉ khi $\left|m\right|\le 1$.

Khi $\left|m\right|\le 1$sẽ tồn tại duy nhất $\alpha \in \left[-\frac{\pi }{2};\frac{\pi }{2}\right]$ thoả mãn $\sin \alpha =m$. Khi đó:

$\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x}=m\iff \sin x=\sin \alpha$ $\iff [\begin{array}{l}x=\alpha +k2\pi \\ x=\pi -\alpha +k2\pi \end{array}\left(k\in \mathbb{Z}\right)$

* Chú ý:

a, Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì $\sin x=\sin {\alpha }^o\iff [\begin{array}{l}x={\alpha }^o+k{360}^o\\ x={180}^o-{\alpha }^o+k{360}^o\end{array}\left(k\in \mathbb{Z}\right)$

b, Một số trường hợp đặc biệt

$\begin{array}{l}\sin x=0\iff x=k\pi ,k\in \mathbb{Z}.\\ \sin x=1\iff x=\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}.\\ \sin x=-1\iff x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}.\end{array}$

3. Phương trình $\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m$

Phương trình $\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m$ có nghiệm khi và chỉ khi $\left|m\right|\le 1$.

Khi $\left|m\right|\le 1$ sẽ tồn tại duy nhất $\alpha \in \left[0;\pi \right]$ thoả mãn $\mathrm{c}\mathrm{o}\mathrm{s}\alpha =m$. Khi đó:

$\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m\iff \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=\mathrm{c}\mathrm{o}\mathrm{s}\alpha$ $\iff [\begin{array}{l}x=\alpha +k2\pi \\ x=-\alpha +k2\pi \end{array}\left(k\in \mathbb{Z}\right)$

* Chú ý:

a, Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì $\cos x=\cos {\alpha }^o\iff [\begin{array}{l}x={\alpha }^o+k{360}^o\\ x=-{\alpha }^o+k{360}^o\end{array}\left(k\in \mathbb{Z}\right)$

b, Một số trường hợp đặc biệt

$\begin{array}{l}\mathrm{c}\mathrm{o}\mathrm{s}x=0\iff x=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}.\\ \mathrm{c}\mathrm{o}\mathrm{s}x=1\iff x=k2\pi ,k\in \mathbb{Z}.\\ \mathrm{c}\mathrm{o}\mathrm{s}x=-1\iff x=\pi +k2\pi ,k\in \mathbb{Z}.\end{array}$

4. Phương trình $\tan x=m$

Phương trình $\tan x=m$có nghiệm với mọi m.

Với mọi $m\in \mathbb{R}$, tồn tại duy nhất $\alpha \in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ thoả mãn $\tan \alpha =m$. Khi đó:

$\tan \mathrm{x}=m\iff \tan x=\tan \alpha \iff x=\alpha +k\pi ,k\in \mathbb{Z}.$

*Chú ý: Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì

$\tan x=\tan {\alpha }^o\iff x={\alpha }^o+k{180}^o,k\in \mathbb{Z}.$

5. Phương trình $\cot x=m$

Phương trình $\cot x=m$có nghiệm với mọi m.

Với mọi $m\in \mathbb{R}$, tồn tại duy nhất $\alpha \in \left(0;\pi \right)$ thoả mãn $\cot \alpha =m$. Khi đó:

$\cot \mathrm{x}=m\iff \cot x=\cot \alpha \iff x=\alpha +k\pi ,k\in \mathbb{Z}.$

*Chú ý: Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì

$\cot x=\cot {\alpha }^o\iff x={\alpha }^o+k{180}^o,k\in \mathbb{Z}.$

6. Sử dụng máy tính cầm tay tìm góc khi biết giá trị lượng giác của nó

Bước 1. Chọn đơn vị đo góc (độ hoặc radian).

Muốn tìm số đo độ, ta ấn: SHIFT $\to$MODE $\to$3 (CASIO FX570VN).

Muốn tìm số đo radian, ta ấn: SHIFT $\to$MODE $\to$4 (CASIO FX570VN).

Bước 2. Tìm số đo góc.

Khi biết SIN, COS, TANG của góc $\alpha$ta cần tìm bằng m, ta lần lượt ấn các phím SHIFT và một trong các phím SIN, COS, TANG rồi nhập giá trị lượng giác m và cuối cùng ấn phím “BẰNG =”. Lúc này trên màn hình cho kết quả là số đo của góc $\alpha$

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Bài 1: Giá trị lượng giác của góc lượng giác

Bài 2: Công thức lượng giác

Bài 3: Hàm số lượng giác

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1