Toán 11 Bài 31 (Kết nối tri thức): Định nghĩa và ý nghĩa của đạo hàm

Giải Toán 11 Bài 31: Định nghĩa và ý nghĩa của đạo hàm

Giải Toán 11 trang 81 Tập 2

Mở đầu trang 81 Toán 11 Tập 2: Nếu một quả bóng được thả rơi tự do từ đài quan sát trên sân thượng của tòa nhà Landmark 81 (Thành phố Hồ Chí Minh) cao 461,3 m xuống mặt đất. Có tính được vận tốc của quả bóng khi nó chạm đất hay không? (Bỏ qua sức cản không khí).

Lời giải:

Sau bài học này, ta giải quyết được bài toán trên như sau:

Ta có thể tính được vận tốc của quả bóng khi nó chạm đất.

Phương trình chuyển động rơi tự do của quả bóng là

s = f(t) = $\frac{1}{2}g{t}^2$

trong đó, g là gia tốc rơi tự do, lấy g = 9,8 m/s²; s (m) là quãng đường nó rơi từ vị trí ban đầu tới mặt đất; t (giây) là thời gian vật rơi từ vị trí ban đầu cho tới khi chạm đất.

Gọi v(t) (m/s) là vận tốc của quả bóng tại thời điểm t. Khi đó v(t) = f'(t) = gt = 9,8t.

Mặt khác, vì chiều cao của tòa nhà là 461,3 m nên quả bóng sẽ chạm đất tại thời điểm t₁, với s = f(t₁) = 461,3 m. Từ đó, ta có

$\frac{1}{2}.9,8t_1^2=461,3\iff t_1=\sqrt{\frac{2.461,3}{9,8}}$ (giây)

Vậy vận tốc của quả bóng khi nó chạm đất là

v(t₁) = 9,8t₁ = 9,8 . $\sqrt{\frac{2.461,3}{9,8}}$ ≈ 95,1 (m/s).s

1. Một số bài toán dẫn đến khái niệm đạo hàm

HĐ1 trang 81 Toán 11 Tập 2: Một vật di chuyển trên một đường thẳng (H.9.2). Quãng đường s của chuyển động là một hàm số của thời gian t, s = s(t) (được gọi là phương trình của chuyển động).

a) Tính vận tốc trung bình của vật trong khoảng thời gian từ t₀ đến t.

b) Giới hạn $\underset{t\to t_0}{\lim }\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}$ cho ta biết điều gì ?

Lời giải:

a)

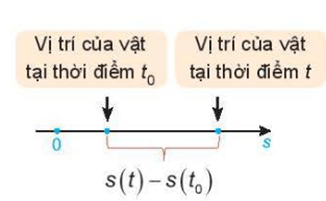
Quãng đường vật đi được trong khoảng thời gian từ t₀ đến t là: s(t) – s(t₀).

Thời gian vật đi được trong khoảng thời gian từ t₀ đến t là: t – t₀.

Vận tốc trung bình của vật trong khoảng thời gian từ t₀ đến t là:

$v=\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}$.

b)

Giới hạn $\underset{t\to t_0}{\lim }\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}$ cho ta biết một điều đó là khi t càng tới gần t₀, có nghĩa là (t – t₀) càng nhỏ thì vận tốc trung bình càng thể hiện được chính xác hơn mức độ nhanh chậm của chuyển động tại thời điểm t₀.

2. Đạo hàm của hàm số tại một điểm

Giải Toán 11 trang 83 Tập 2

Luyện tập 1 trang 83 Toán 11 Tập 2: Tính đạo hàm của hàm số y = –x² + 2x + 1 tại điểm x₀ = –1.

Lời giải:

Đặt f(x) = y = –x² + 2x + 1.

Ta có: f(x) – f(– 1) = – x² + 2x + 1 – [– (– 1)² + 2 . (– 1) + 1] = – x² + 2x + 3.

Với x ≠ – 1, ta có $\frac{f\left(x\right)-f\left(-1\right)}{x-\left(-1\right)}=\frac{-x^2+2x+3}{x+1}=\frac{(x+1)(3-x)}{x+1}=3-x$ .

Khi đó, $\underset{x\to -1}{\lim }\frac{f\left(x\right)-f(-1)}{x-(-1)}=\underset{x\to -1}{\lim }\frac{-x^2+2x+3}{x+1}=\underset{x\to -1}{\lim }\left(3-x\right)=4$ .

Vậy đạo hàm của hàm số y = –x² + 2x + 1 tại điểm x₀ = –1 có giá trị là 4.

3. Đạo hàm của hàm số trên một khoảng

HĐ3 trang 83 Toán 11 Tập 2: Tính đạo hàm f'(x₀) tại điểm x₀ bất kì trong các trường hợp sau:

a) f(x) = c (c là hằng số);

b) f(x) = x.

Lời giải:

a) Ta có f(x) = c nên f(x) = f(x₀) = c.

Khi đó, $f\text{'}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{c-c}{x-x_0}=\underset{x\to x_0}{\lim }0=0$ .

b) Ta có f(x) = x nên f(x₀) = x₀.

Khi đó, $f\text{'}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{x-x_0}{x-x_0}=1$ .

Giải Toán 11 trang 84 Tập 2

Luyện tập 2 trang 84 Toán 11 Tập 2:

a) y = x² + 1

b) y = kx + c (với k, c là các hằng số).

Lời giải:

a) Đặt f(x) = y = x² + 1.

Ta có:

$f\text{'}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{x^2+1-(x_0^2+1)}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{(x-x_0)(x+x_0)}{x-x_0}=\underset{x\to x_0}{\lim }\left(x+x_0\right)=2x_0$.

Vậy hàm số y = x² + 1 có đạo hàm là hàm số y' = 2x.

b) Đặt f(x) = y = kx + c (với k, c là các hằng số).

Ta có:

$f\text{'}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{kx+c-(k{x}_0+c)}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{k(x-x_0)}{x-x_0}=\underset{x\to x_0}{\lim }k=k$.

Vậy hàm số y = kx + c (với k, c là các hằng số) có đạo hàm là hàm số y' = k.

4. Ý nghĩa hình học của đạo hàm

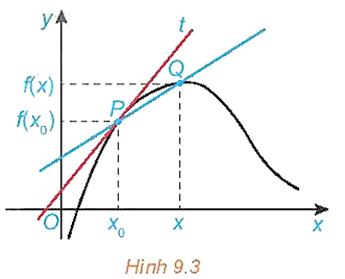
HĐ4 trang 84 Toán 11 Tập 2: Nhận biết tiếp tuyến của đồ thị hàm số

Cho hàm số y = f(x) có đồ thị (C) và P(x₀; f(x₀)) ∈ (C). Xét điểm Q(x; f(x)) thay đổi trên (C) với x ≠ x₀.

a) Đường thẳng đi qua hai điểm P, Q được gọi là một cát tuyến của đồ thị (C) (H.9.3). Tìm hệ số góc k_PQ của cát tuyến PQ.

b) Khi x → x₀ thì vị trí của điểm Q(x; f(x)) trên đồ thị (C) thay đổi như thế nào ?

c) Nếu điểm Q di chuyển trên (C) tới điểm P mà k_PQcó giới hạn hữu hạn k thì có nhận xét gì về vị trí giới hạn của cát tuyến QP?

Lời giải:

a) Ta có: $\overrightarrow{PQ}=\left(x-x_0;f\left(x\right)-f\left(x_0\right)\right)$ . Suy ra ${\overrightarrow{n}}_{PQ}=\left(f\left(x\right)-f\left(x_0\right);x_0-x\right)$ .

Phương trình đường thẳng PQ là

[f(x) – f(x₀)](x – x₀) + (x_0­ – x)[y – f(x₀)] = 0

Hay [f(x) – f(x₀)]x – (x – x₀)y – f(x)x₀ + xf(x₀) = 0

Tức là y = $\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}x+\frac{xf\left(x_0\right)-x_{0}f\left(x\right)}{x-x_0}$ .

Do đó, hệ số góc của cát tuyến PQ là $k_{PQ}=\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$ .

b)

Khi x$\to$x_o thì vị trí của điểm Q(x; f(x)) trên đồ thị (C) sẽ tiến gần đến điểm P(x₀; f(x₀)) và khi x = x₀ hai điểm này sẽ trùng nhau.

c)

Nếu điểm Q di chuyển trên (C) tới điểm P mà k_PQ có giới hạn hữu hạn k thì cát tuyến PQ cũng sẽ tiến gần đến gần vị trí tiếp tuyến của đồ thị (C) tại điểm P. Vì vậy giới hạn của cát tuyến QP sẽ là đường thẳng tiếp tuyến tại điểm P.

Giải Toán 11 trang 85 Tập 2

Luyện tập 3 trang 85 Toán 11 Tập 2: Tìm hệ số góc của tiếp tuyến của parabol y = x² tại điểm có hoành độ x₀ = $\frac{1}{2}$ .

Lời giải:

Ta có: y' = (x²)' = 2x nên $y^{\text{'}}\left(\frac{1}{2}\right)=2.\frac{1}{2}=1$ .

Vậy hệ số của tiếp tuyến của parabol y = x² tại điểm có hoành độ x₀ = $\frac{1}{2}$ là k = 1.

HĐ5 trang 85 Toán 11 Tập 2: Cho hàm số y = x² có đồ thị là đường parabol (P).

a) Tìm hệ số góc của tiếp tuyến (P) tại điểm có hoành độ x₀ = 1.

b) Viết phương trình tiếp tuyến đó.

Lời giải:

a)

Ta có: y' = (x²)' = 2x nên y'(1) = 2.1 = 2.

Vậy hệ số góc của tiếp tuyến của parabol y = x² tại điểm có hoành độ x₀ = 1 là k = 2.

b)

Ta có: x₀ = 1 nên y₀ = 1² = 1.

Hệ số góc của tiếp tuyến là k = 2 nên phương trình tiếp tuyến có dạng y = 2x + c.

Suy ra: 1 = 2.1 + c ⇒ c = –1.

Vậy phương trình tiếp tuyến là y = 2x – 1.

Luyện tập 4 trang 85 Toán 11 Tập 2: Viết phương trình tiếp tuyến của parabol (P): y = –2x² tại điểm có hoành độ x₀ = –1.

Lời giải:

Ta có: y' = (–2x²) = –4x.

Nên hệ số góc của tiếp tuyến tại điểm có hoành độ x₀ = –1 là y'(–1) = –4.(–1) = 4.

Ngoài ra, ta có y(–1) = –2 nên phương trình tiếp tuyến cần tìm là:

y – (–2) = 4(x + 1) hay y = 4x + 2.

Vận dụng trang 85 Toán 11 Tập 2: Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là 400 m (H.9.4). Độ dốc của mặt cầu không vượt quá 10^o(độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc với mặt cầu và phương ngang như Hình 9.5). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

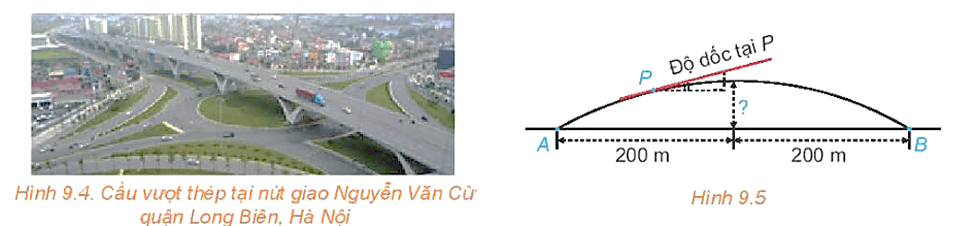
Chọn hệ trục tọa độ Oxy sao cho O là trung điểm AB. Tia Ox trùng với tia OB, tia Oy vuông góc với tia Ox tại O, hướng như hình vẽ.

Khi đó ta có: A(–200; 0); B(200; 0).

Gọi chiều cao giới hạn của cầu là h (h > 0), suy ra đỉnh cầu có tọa độ (0; h).

Ta tìm được phương trình parabol của cầu là: $y=\frac{-h}{{200}^2}{x}^2+h$.

Theo cách làm ở Ví dụ 2, ta có: $y\text{'}=\frac{-2h}{{200}^2}x$ .

Suy ra hệ số góc xác định độ dốc của mặt cầu là:

k = $y\text{'}=\frac{-2h}{{200}^2}x$ với –200 ≤ x ≤ 200

Do đó, |k| = $\frac{-2h}{{200}^2}$|x| ≤ $\frac{-2h}{{200}^2}$.200 = $\frac{h}{100}$.

Vì độ dốc của mặt cầu không quá nên ta có: $\frac{h}{100}$≤ tan10^o ⇔ h ≤ 17,6.

Vậy chiều cao giới hạn từ đỉnh cầu tới mặt đường là 17,6 m.

Bài tập

Giải Toán 11 trang 86 Tập 2

Bài 9.1 trang 86 Toán 11 Tập 2: Tính (bằng định nghĩa) đạo hàm của các hàm số sau:

a) y = x² – x tại x₀ = 1;

b) y = –x³ tại x₀ = –1.

Lời giải:

a)

Ta có: f'(1) = $\underset{x\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}=\underset{x\to 1}{\lim }\frac{x^2-x}{x-1}=\underset{x\to 1}{\lim }\frac{x\left(x-1\right)}{x-1}=\underset{x\to 1}{\lim }x=1$ .

Vậy f'(1) = 1.

b)

Ta có:

f'(–1) = $\underset{x\to -1}{\lim }\frac{f\left(x\right)-f(-1)}{x-(-1)}=\underset{x\to -1}{\lim }\frac{-x^3-1}{x+1}=\underset{x\to -1}{\lim }\frac{-\left(x+1\right)\left(x^2-x+1\right)}{x+1}$

= $=\underset{x\to -1}{\lim }$[-(x²-x+1)] = -3

Vậy f'(–1) = – 3.

Bài 9.2 trang 86 Toán 11 Tập 2: Sử dụng định nghĩa, tính đạo hàm của các hàm số sau:

a) y = kx² + c (với k, c là các hằng số);

b) y = x³.

Lời giải:

a) Đặt y = f(x) = kx² + c.

Với x₀ bất kì, ta có:

f'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{k{x}^2+c-(k{x_0}^2+c)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{k(x^2-{x_0}^2)}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{k(x-x_0)(x+x_0)}{x-x_0}=\underset{x\to x_0}{\lim }$[k(x+x₀)] = 2kx₀.

Vậy hàm số y = kx² + c có đạo hàm là hàm số y' = 2kx.

b) Đặt y = f(x) = x³.

Với x₀ bất kì, ta có:

f'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{x^3-{x_0}^3}{x-x_0}=\underset{x\to x_0}{\lim }\frac{(x-x_0)(x^2+x{x}_0+{x_0}^2)}{x-x_0}$

$=\underset{x\to x_0}{\lim }(x^2+x{x}_0+{x_0}^2)=3{x_0}^2$

Vậy hàm số y = x³ có đạo hàm là hàm số y' = 3x².

Bài 9.3 trang 86 Toán 11 Tập 2: Viết phương trình tiếp tuyến của parabol y = –x² + 4x, biết:

a) Tiếp điểm có hoành độ x₀ = 1;

b) Tiếp điểm có tung độ y₀ = 0.

Lời giải:

Đặt y = f(x) = – x² + 4x.

Với x₀ bất kì, ta có:

f'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{-x^2+4x+{x_0}^2-4x_0}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{-\left(x^2-{x_0}^2\right)+4\left(x-x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{\left(x-x_0\right)\left(-x-x_0+4\right)}{x-x_0}$

$=\underset{x\to x_0}{\lim }(-x-x_0+4)=-2x_0+4$.

Vậy hàm số y = –x² + 4x có đạo hàm là hàm số y' = –2x + 4.

a)

Ta có: y'(1) = –2.1 + 4 = 2.

Ngoài ra, f(1) = 3 nên phương trình tiếp tuyến cần tìm là:

y – 3 = 2(x – 1) hay y = 2x + 1.

b)

Ta có: y₀ = 0 nên –x₀² + 4x₀ = 0 ⇔ .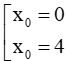

+) Với x₀ = 0, y₀ = 0, ta có y'(0) = 4, do đó phương trình tiếp tuyến cần tìm là y = 4x.

+) Với x₀ = 4, y₀ = 0, ta có y'(4) = –4 do đó phương trình tiếp tuyến cần tìm là:

y = –4(x – 4) hay y = –4x + 16.

Bài 9.4 trang 86 Toán 11 Tập 2: Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19,6 m/s thì độ cao h của nó (tính bằng mét) sau t giây được cho bởi công thức h = 19,6t – 4,9t². Tìm vận tốc của vật khi nó chạm đất.

Lời giải:

+ Đặt h = f(t) = 19,6t – 4,9t².

Với x₀ bất kì, ta có:

$f\text{'}\left(t_0\right)=\underset{t\to t_0}{\lim }\frac{f\left(t\right)-f\left(t_0\right)}{t-t_0}=\underset{t\to t_0}{\lim }\frac{19,6t-4,9t^2-19,6t_0+4,9{t_0}^2}{t-t_0}$

$=\underset{t\to t_0}{\lim }\frac{-4,9\left(t^2-{t_0}^2\right)+19,6\left(t-t_0\right)}{t-t_0}=\underset{t\to t_0}{\lim }\frac{\left(t-t_0\right)\left(-4,9t-4,9t_0+19,6\right)}{t-t_0}$

$=\underset{t\to t_0}{\lim }\left(-4,9t-4,9t_0+19,6\right)=-9,8t_0+19,6$.

Vậy hàm số h = 19,6t – 4,9t² có đạo hàm là hàm số h' = –9,8t₀ + 19,6.

+ Khi vật chạm đất thì h = 0, tức là 19,6t – 4,9t² = 0 ⇔ .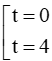

Khi t = 4, vận tốc của vật khi nó chạm đất là v(4) = h'(4) = –9,8.4 + 19,6 = –19,6 (m/s).

Bài 9.5 trang 86 Toán 11 Tập 2: Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên L₁ và đoạn dốc xuống L₂ là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, L₁ và L₂ phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc tọa độ đặt tại P và phương trình của parabol là y = ax² + bx + c, trong đó x tính bằng mét.

a) Tìm c.

b) Tính y'(0) và tìm b.

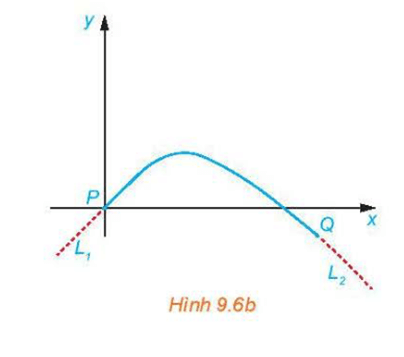
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.

d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.

Lời giải:

a)

Vì gốc tọa độ đặt tại P nên P(0; 0) do đó ta có: c = y(0) = 0.

b)

Ta tính được: y' = 2ax + b.

Suy ra: y'(0) = b.

Mà L₁ là phương trình tiếp tuyến tại P có hệ số góc 0,5 nên y'(0) = 0,5 ⇒ b = 0,5.

c)
L₂ là phương trình tiếp tuyến tại Q có hệ số góc –0,75 nên

y'(x_Q) = 2ax_Q + 0,5 = –0,75.

Vì khoảng cách theo phương ngang giữa P và Q là 40 m nên x_Q – x_P = x_Q = 40.

⇒ 2a . 40 + 0,5 = –0,75 ⇒ a = $\frac{-1}{64}$ .

Khi đó phương trình parabol là $y=-\frac{1}{64}{x}^2+\frac{1}{2}x$ .

d)

Ta có: $y_Q=\frac{-1}{64}{.40}^2+\frac{1}{2}.40=-5$.

Vậy chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q là: |y_P – y_Q| = 5.

Lý thuyết Định nghĩa và ý nghĩa của đạo hàm

1. Đạo hàm của hàm số tại một điểm

- Định nghĩa: Cho hàm số y = f(x) xác định trên khoảng $\left(a;b\right)$ và điểm $x_0\in \left(a;b\right)$. Nếu tồn tại giới hạn (hữu hạn)

$\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$

thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm $x_0$, kí hiệu là $f^{\prime }\left(x_0\right)$ hoặc $y^{\prime }\left(x_0\right)$.

- Cách viết khác của định nghĩa:

$f^{\prime }\left(x_0\right)=\underset{h\to 0}{lim}\frac{f\left(x_0+h\right)-f\left(x_0\right)}{h}$.

- Quy tắc tính đọa hàm của hàm số tại một điểm bằng định nghĩa:

Bước 1: Tính $f\left(x\right)-f\left(x_0\right)$.

Bước 2: Lập và rút gọn tỉ số $\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$ với $x\in \left(a;b\right),x\ne x_0$.

Bước 3: Tìm giới hạn $\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$.

2. Đạo hàm của hàm số trên một khoảng

Hàm số y = f(x) được gọi là đạo hàm trên khoảng (a; b) nếu nó có đạo hàm f’(x) tại mọi điểm x thuộc khoảng đó, kí hiệu là y’ = f’(x).

3. Ý nghĩa hình học của đạo hàm

- Hệ số góc tiếp tuyến của đồ thị hàm số y = f(x) tại điểm $M\left(x_0;f\left(x_0\right)\right)$ là $k=f^{\prime }\left(x_0\right)$ nếu đạo hàm $f^{\prime }\left(x_0\right)$ tồn tại.

- Phương tình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm $M\left(x_0;y_0\right)$, $y_0=f\left(x_0\right)$ là:

$y-y_0=f^{\prime }\left(x_0\right)\left(x-x_0\right)$.

4. Ý nghĩa vật lí của đạo hàm

Vận tốc tức thời của chuyển động s = s(t) tại thời điểm t là v(t) = s’(t).

Sơ đồ tư duy Định nghĩa và ý nghĩa của đạo hàm

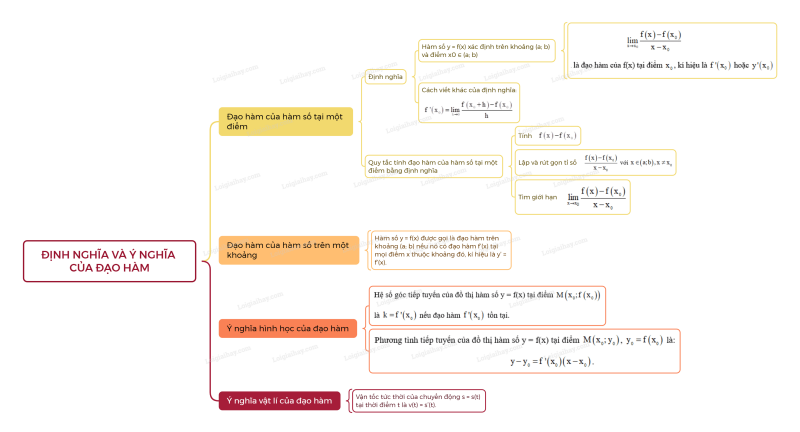
Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 8 trang 79

Bài 32: Các quy tắc tính đạo hàm

Bài 33: Đạo hàm cấp hai

Bài tập cuối chương 9 trang 97

Một vài mô hình toán học sử dụng hàm số mũ và hàm số lôgarit