Toán 11 Bài 29 (Kết nối tri thức): Công thức cộng xác suất

Giải Toán 11 Bài 29: Công thức cộng xác suất

Giải Toán 11 trang 72 Tập 2

Mở đầu trang 72 Toán 11 Tập 2: Tại tỉnh X, thống kê cho thấy trong số những người trên 50 tuổi có 8,2% mắc bệnh tim; 12,5% mắc bệnh huyết áp và 5,7% mắc cả bệnh tim và bệnh huyết áp. Từ đó, ta có thể tính được tỉ lệ dân cư trên 50 tuổi của tỉnh X mắc cả bệnh tim và huyết áp hay không ?

Lời giải:

Từ các dữ kiện của đề bài, ta có thể tính được tỉ lệ dân cư trên 50 tuổi của tỉnh X mắc cả bệnh tim và huyết áp dựa vào các công thức cộng xác suất.

1. Công thức cộng xác suất cho hai biến có xung khắc

HĐ1 trang 72 Toán 11 Tập 2: Gieo một con xúc xắc cân đối, đồng chất. Xét hai biến cố sau:

A: “Số chấm xuất hiện trên con xúc xắc là số chia hết cho 3”;

B: “Số chấm xuất hiện trên con xúc xắc là số chia hết cho 4”.

Hai biến cố A và B có đồng thời xảy ra hay không ? Vì sao ?

Lời giải:

Ta có:

A = {3; 6}

B = {4}

Do đó, A ∩ B = ∅.

Vậy hai biến cố A và B không thể đồng thời xảy ra.

Câu hỏi trang 72 Toán 11 Tập 2: Biến cố A và biến cố đối $\overline{A}$ có xung khắc hay không ? Tại sao ?

Lời giải:

Biến cố A và biến cố đối $\overline{A}$ có xung khắc. Vì A ∩ $\overline{A}$ = ∅.

Giải Toán 11 trang 73 Tập 2

Luyện tập 1 trang 73 Toán 11 Tập 2: Một tổ học sinh có 8 bạn, trong đó có 6 bạn thích môn Bóng đá, 4 bạn thích môn Cầu lông và 2 bạn thích cả hai môn Bóng đá và Cầu lông. Chọn ngẫu nhiên một học sinh trong tổ. Xét các biến cố sau:

E: “Học sinh được chọn thích môn Bóng đá”;

F: “Học sinh được chọn thích môn Cầu lông”.

Hai biến cố E và F có xung khắc không ?

Lời giải:

Hai biến cố E và F không xung khắc vì nếu bạn được chọn là một trong hai bạn thích cả hai môn Bóng đá và Cầu lông thì cả E và F đều xảy ra.

HĐ2 trang 73 Toán 11 Tập 2: Trở lại tình huống trong HĐ1. Hãy tính P(A), P(B) và P(A∪ B).

Lời giải:

Không gian mẫu: Ω = {1; 2; 3; 4; 5; 6}.

Ta có:

A = {3; 6}. Suy ra: P(A) = $\frac{2}{6}=\frac{1}{3}$ .

B = {4}. Suy ra: P(B) = $\frac{1}{6}$ .

A ∪ B = {3; 4; 6}. Suy ra: P(A∪ B) = $\frac{3}{6}=\frac{1}{2}$ .

Giải Toán 11 trang 74 Tập 2

Luyện tập 2 trang 74 Toán 11 Tập 2: Một hộp đựng 5 quả cầu màu xanh và 3 quả cầu màu đỏ, có cùng kích thước và khối lượng. Chọn ngẫu nhiên hai quả cầu trong hộp. Tính xác suất để chọn được hai quả cầu có cùng màu.

Lời giải:

Gọi A là biến cố “Chọn được hai quả cầu màu xanh”; B là biến cố “Chọn được hai quả cầu màu đỏ”; C là biến cố “Chọn được hai quả cầu có cùng màu”.

Biến cố C xảy ra khi và chỉ khi hai quả cầu được chọn có cùng màu đỏ hoặc có cùng màu xanh. Biến cố A xảy ra khi hai quả cầu được chọn có cùng màu xanh. Biến cố B xảy ra khi hai quả cầu được chọn có cùng màu đỏ. Vậy C là biến cố hợp của A và B hay C = A∪ B.

Vì A và B là hai biến cố xung khắc nên ta có:

P(C) = P(A ∪ B) = P(A) + P(B).

Do đó, ta cần tính P(A) và P(B).

Không gian mẫu Ω là tập hợp gồm các tập con có hai phần tử của tập có 5 + 3 = 8 phần tử. Do đó, n(Ω) = $C_8^2$ = 28.

Tính P(A):

Biến cố A là tập hợp gồm các tập con có hai phần tử của tập có 5 phần tử (5 quả cầu màu xanh). Do đó, n(A) = $C_5^2$ = 10. Suy ra, P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{10}{28}=\frac{5}{14}$ .

Tính P(B):

Biến cố B là tập hợp gồm các tập con có hai phần tử của tập có 3 phần tử (3 quả cầu màu đỏ). Do đó, n(B) = $C_3^2$ = 3. Suy ra, P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{3}{28}$.

Vậy P(C) = P(A) + P(B) = $\frac{5}{14}+\frac{3}{28}=\frac{13}{28}$ .

2. Công thức cộng xác suất

HĐ3 trang 74 Toán 11 Tập 2: Ở một trường trung học phổ thông X, có 19% học sinh học khá môn Ngữ văn, 32% học sinh học khá môn Toán, 7% học sinh học khá cả hai môn Ngữ văn và Toán. Chọn ngẫu nhiên một học sinh của trường X. Xét hai biến cố sau:

A: “Học sinh đó học khá môn Ngữ văn”;

B: “Học sinh đó học khá môn Toán”.

a) Hoàn thành các mệnh đề sau bằng cách tìm cụm từ thích hợp thay cho dấu “?”.

P(A) là tỉ lệ …(?)… P(AB) là tỉ lệ …(?)…

P(B) là …(?)… P(A∪ B) là …(?)…

b) Tại sao để tính P(A∪ B) ta không áp dụng được công thức P(A ∪ B) = P(A) + P(B)?

Lời giải:

a)

P(A) là tỉ lệ học sinh học khá môn Ngữ văn;

P(B) là tỉ lệ học sinh học khá môn Toán;

P(AB) là tỉ lệ học sinh học khá cả hai môn Ngữ văn và Toán;

P(A∪ B) là tỉ lệ học sinh học khá môn Ngữ văn hoặc học khá môn Toán.

b)

Để tính P(A∪ B) ta không áp dụng được công thức P(A∪ B) = P(A) + P(B) vì hai biến cố A và B không xung khắc, nếu học sinh được chọn nằm trong 7% học sinh học khá cả hai môn Ngữ văn và Toán thì cả A và B cùng xảy ra.

Câu hỏi trang 74 Toán 11 Tập 2: Tại sao công thức cộng xác suất cho hai biến cố xung khắc là hệ quả của công thức cộng xác suất ?

Lời giải:

Công thức cộng xác suất:

P(A∪ B) = P(A) + P(B) – P(AB)

Khi hai biến cố A và B xung khắc thì A ∩ B = nên P(AB) = 0, do đó, công thức cộng xác suất trở thành: P(A∪ B) = P(A) + P(B) – 0 = P(A) + P(B). Đây chính là công thức cộng xác suất cho hai biến cố xung khắc.

Vậy công thức cộng xác suất cho hai biến cố xung khắc là hệ quả của công thức cộng xác suất.

Giải Toán 11 trang 75 Tập 2

Luyện tập 3 trang 75 Toán 11 Tập 2: Phỏng vấn 30 học sinh lớp 11A về môn thể thao yêu thích thu được kết quả có 19 bạn thích môn Bóng đá, 17 bạn thích môn Bóng bàn và 15 bạn thích cả hai môn đó. Chọn ngẫu nhiên một học sinh lớp 11A. Tính xác suất để chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn.

Lời giải:

Gọi A là biến cố “Học sinh được chọn thích môn Bóng đá”; biến cố B là biến cố “Học sinh được chọn thích môn Bóng bàn”.

Biến cố “Học sinh được chọn thích cả hai môn Bóng đá và Bóng bàn” là biến cố giao của A và B.

Biến cố C là biến cố “Chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn” xảy ra khi và học sinh được chọn thích Bóng đá hoặc học sinh được chọn thích Bóng bàn. Do đó, C là biến cố hợp của A và B.

Áp dụng công thức cộng xác suất ta có:

P(C) = P(A ∪ B) = P(A) + P(B) – P(AB).

Ta cần tính: P(A), P(B), P(AB)

Không gian mẫu Ω là tập hợp học sinh lớp 11A nên n(Ω) = 30.

Tính P(A):

Biến cố A là tập hợp học sinh thích môn Bóng đá nên n(A) = 19.

Suy ra: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{19}{30}$ .

Tính P(B):

Biến cố B là tập hợp học sinh thích môn Bóng bàn nên n(B) = 17.

Suy ra: P(B) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{17}{30}$ .

Tính P(AB):

Biến cố “Học sinh được chọn thích cả hai môn Bóng đá và Bóng bàn” là biến cố giao của A và B nên n(AB) = 15.

Suy ra: P(AB) = $\frac{n\left(AB\right)}{n\left(\Omega \right)}=\frac{15}{30}=\frac{1}{2}$ .

Vậy P(C) = P(A∪ B) = P(A) + P(B) – P(AB) = $\frac{19}{30}+\frac{17}{30}-\frac{1}{2}=\frac{7}{10}=0,7$ .

Vậy xác suất để chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn là 0,7.

Vận dụng trang 75 Toán 11 Tập 2: Giải quyết bài toán trong tình huống mở đầu.

Gợi ý. Chọn ngẫu nhiên một người dân trên 50 tuổi của tỉnh X. Gọi A là biến cố “Người đó mắc bệnh tim”; B là biến cố “Người đó mắc bệnh huyết áp”; E là biến cố “Người đó không mắc cả bệnh tim và bệnh huyết áp”. Khi đó $\overline{E}$ là biến cố “Người đó mắc bệnh tim hoặc mắc bệnh huyết áp”. Ta có: $\overline{E}$ = A∪ B. Áp dụng công thức cộng xác suất và công thức xác suất của biến cố đối để tính P(E).

Lời giải:

Chọn ngẫu nhiên một người dân trên 50 tuổi của tỉnh X. Gọi A là biến cố “Người đó mắc bệnh tim”; B là biến cố “Người đó mắc bệnh huyết áp”; E là biến cố “Người đó không mắc cả bệnh tim và bệnh huyết áp”.

Khi đó $\overline{E}$ là biến cố “Người đó mắc bệnh tim hoặc mắc bệnh huyết áp”. Biến cố “Người đó mắc cả bệnh tim và bệnh huyết áp” là biến cố giao của A và B.

Ta có: $\overline{E}$ = A∪ B.

Áp dụng công thức cộng xác suất ta có:

P($\overline{E}$) = P(A ∪ B) = P(A) + P(B) – P(AB)

Áp dụng công thức xác suất của biến cố đối ta có:

P(E) = 1 – P($\overline{E}$).

Do đó, ta cần tính P(A), P(B), P(AB).

Ta có:

P(A) = 8,2% = 0,082

P(B) = 12,5% = 0,125

P(AB) = 5,7% = 0,057

Suy ra P($\overline{E}$) = P(A∪ B) = P(A) + P(B) – P(AB) = 0,082 + 0,125 – 0,057 = 0,15.

Do đó P(E) = 1 – P($\overline{E}$) = 1 – 0,15 = 0,85.

Vậy tỉ lệ dân cư trên 50 tuổi của tỉnh X không mắc cả bệnh tim và bệnh huyết áp là 85%.

Bài tập

Bài 8.6 trang 75 Toán 11 Tập 2: Một hộp đựng 8 viên bi màu xanh và 6 viên bi màu đỏ, có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một viên bi từ hộp (lấy xong không trả lại vào hộp). Tiếp đó đến lượt bạn Tùng lấy ngẫu nhiên một viên bi từ hộp đó. Tính xác suất để bạn Tùng lấy được viên bi màu xanh.

Lời giải:

Gọi A là biến cố “Bạn Sơn lấy được viên bi màu xanh, bạn Tùng lấy được viên bi màu xanh”; B là biến cố “Bạn Sơn lấy được viên bi màu đỏ, bạn Tùng lấy được viên bi màu xanh”.

Do đó, biến cố “bạn Tùng lấy được viên bi màu xanh” là biến cố hợp của A và B.

Vì A và B là hai biến cố xung khắc nên ta áp dụng công thức cộng xác suất cho hai biến cố xung khắc có:

P(A∪ B) = P(A) + P(B).

+ Không gian mẫu Ω:

Hộp bao gồm: 6 + 8 = 14 viên bi

Mỗi phần tử của Ω được chọn bởi hai công đoạn:

Công đoạn 1: Bạn Sơn lấy ngẫu nhiên một viên bi từ hộp (lấy xong không trả lại vào hộp). Có $C_{14}^1$ = 14 (cách chọn).

Công đoạn 2: Sau công đoạn 1, hộp còn lại 13 viên bi. Bạn Tùng lấy lấy ngẫu nhiên một viên bi từ hộp đó. Có $C_{13}^1$ = 13 (cách chọn)

Theo quy tắc nhân, ta có: n(Ω) = 14 . 13 = 182.

+ Tính P(A):

Mỗi phần tử của A được chọn bởi hai công đoạn:

Công đoạn 1: Bạn Sơn lấy ngẫu nhiên một viên bi trong 8 viên bi màu xanh từ hộp (lấy xong không trả lại vào hộp). Có 8 cách chọn.

Công đoạn 2: Bạn Tùng lấy ngẫu nhiên một viên bi trong 7 viên bi màu xanh còn lại trong hộp đó. Có 7 cách chọn.

Theo quy tắc nhân, ta có: n(A) = 8 . 7 = 56.

Suy ra: P(A) = $\frac{56}{182}=\frac{4}{13}$ .

+ Tính P(B):

Mỗi phần tử của B được chọn bởi hai công đoạn:

Công đoạn 1: Bạn Sơn lấy ngẫu nhiên một viên bi trong 6 viên bi màu đỏ từ hộp (lấy xong không trả lại vào hộp). Có 6 cách chọn.

Công đoạn 2: Bạn Tùng lấy ngẫu nhiên một viên bi trong 8 viên bi màu xanh còn lại trong hộp đó. Có 8 cách chọn.

Theo quy tắc nhân, ta có: n(B) = 6 . 8 = 48.

Suy ra: P(B) = $\frac{48}{182}=\frac{24}{91}$ .

Do đó, ta có: P(A∪ B) = P(A) + P(B) = $\frac{4}{13}+\frac{24}{91}=\frac{4}{7}$ .

Vậy xác suất để bạn Tùng lấy được viên bi màu xanh là $\frac{4}{7}$ .

Bài 8.7 trang 75 Toán 11 Tập 2: Lớp 11A của một trường có 40 học sinh, trong đó có 14 bạn thích nhạc cổ điển, 13 bạn thích nhạc trẻ và 5 bạn thích cả nhạc cổ điển và nhạc trẻ. Chọn ngẫu nhiên một bạn trong lớp. Tính xác suất để:

a) Bạn đó thích nhạc cổ điển hoặc nhạc trẻ;

b) Bạn đó không thích cả nhạc cổ điển và nhạc trẻ.

Lời giải:

Gọi A là biến cố “Bạn đó thích nhạc cổ điển”; B là biến cố “Bạn đó thích nhạc trẻ”; C là biến cố “Bạn đó thích nhạc cổ điển hoặc nhạc trẻ”. Biến cố “Bạn đó thích cả nhạc cổ điển và nhạc trẻ” là biến cố giao của A và B.

Do đó, ta có: C = A∪ B.

Biến cố $\overline{C}$ là biến cố “Bạn đó không thích cả nhạc cổ điển và nhạc trẻ”.

a)

Áp dụng công thức cộng xác suất ta có:

P(C) = P(A∪ B) = P(A) + P(B) – P(AB)

Ta cần tính: P(A), P(B), P(AB).

+ Không gian mẫu Ω là tập hợp các học sinh của lớp 11A nên n(Ω) = 40.

+ Tính P(A):

Biến cố A là tập hợp các học sinh thích nhạc cổ điển nên n(A) = 14.

Suy ra: P(A) = $\frac{14}{40}=\frac{7}{20}$ .

+ Tính P(B):

Biến cố B là tập hợp các học sinh thích nhạc trẻ nên n(B) = 13.

Suy ra: P(B) = $\frac{13}{40}$ .

+ Tính P(AB):

Biến cố giao của A và B là tập hợp các học sinh thích cả nhạc cổ điển và nhạc trẻ nên n(AB) = 5.

Suy ra: P(AB) = $\frac{5}{40}=\frac{1}{8}$ .

Do đó, P(C) = P(A) + P(B) – P(AB) = $\frac{7}{20}+\frac{13}{40}-\frac{1}{8}=\frac{11}{20}$ .

Vậy xác suất để bạn được chọn thích nhạc cổ điển hoặc nhạc trẻ là $\frac{11}{20}$ .

b)

Áp dụng công thức tính xác suất của biến cố đối ta có:

P($\overline{C}$) = 1 – P(C) = 1 – $\frac{11}{20}$ = $\frac{9}{20}$.

Vậy xác suất để bạn được chọn không thích cả nhạc cổ điển và nhạc trẻ là $\frac{9}{20}$.

Bài 8.8 trang 75 Toán 11 Tập 2: Một khu phố có 50 hộ gia đình nuôi chó hoặc nuôi mèo, trong đó có 18 hộ nuôi chó, 16 hộ nuôi mèo và 7 hộ nuôi cả chó và mèo. Chọn ngẫu nhiên một hộ trong khu phố trên. Tính xác suất để:

a) Hộ đó nuôi chó hoặc nuôi mèo;

b) Hộ đó không nuôi cả chó và mèo.

Lời giải:

Gọi A là biến cố “Hộ đó nuôi chó” ; B là biến cố “Hộ đó nuôi mèo” ; C là biến cố “Hộ đó nuôi cả chó và mèo” ; D là biến cố “Hộ đó nuôi chó hoặc nuôi mèo”.

Như vậy, ta có:

C = A ∩ B; D = A∪ B.

$\overline{D}$ là biến cố đối của D, tức là $\overline{D}$ là biến cố “Hộ đó không nuôi cả chó và mèo”.

a)

Áp dụng công thức cộng xác suất ta có:

P(D) = P(A∪ B) = P(A) + P(B) – P(AB) = P(A) + P(B) – P(C)

Ta cần tính P(A), P(B), P(C)

+ Không gian mẫu Ω là tập hợp 50 hộ gia đình nên n(Ω) = 50.

+ Tính P(A):

Biến cố A là tập hợp các hộ gia đình nuôi chó nên n(A) = 18.

Suy ra: P(A) = $\frac{18}{50}=\frac{9}{25}$ .

+ Tính P(B):

Biến cố B là tập hợp các hộ gia đình nuôi mèo nên n(B) = 16.

Suy ra: P(B) = $\frac{16}{50}=\frac{8}{25}$ .

+ Tính P(C):

Biến cố C là tập hợp các hộ gia đình nuôi cả chó và mèo nên n(C) = 7.

Suy ra: P(C) = $\frac{7}{50}$ .

Do đó, ta có: P(D) = P(A) + P(B) – P(C) = $\frac{9}{25}+\frac{8}{25}-\frac{7}{50}=\frac{27}{50}$ .

Vậy xác suất để hộ được chọn nuôi chó hoặc mèo là $\frac{27}{50}$.

b)

Áp dụng công thức tính xác suất cho biến cố đối ta có:

P( ) = 1 – P(D) = 1 – $\frac{27}{50}$ = $\frac{23}{50}$ .

Vậy xác suất để hộ được chọn không nuôi cả chó và mèo là $\frac{23}{50}$ .

Bài 8.9 trang 75 Toán 11 Tập 2: Một nhà xuất bản phát hành hai cuốn sách A và B. Thống kê cho thấy 50% người mua sách A; 70% người mua sách B; 30% người mua cả sách A và sách B. Chọn ngẫu nhiên một người mua. Tính xác suất để:

a) Người mua đó mua ít nhất một trong hai sách A hoặc B;

b) Người mua đó không mua cả sách A và sách B.

Lời giải:

a)

Gọi E là biến cố “Người đó mua cuốn sách A”; F là biến cố “Người đó mua cuốn sách B” ; G là biến cố “Người đó mua cả hai cuốn sách A và B”; H là biến cố “Người đó mua ít nhất một trong hai sách A và B”.

Như vậy ta có:

G = E ∩ F ; H = E∪ F.

Áp dụng công thức cộng xác suất ta có:

P(H) = P(E∪ F) = P(E) + P(F) – P(EF) = P(E) + P(F) – P(G)

Lại có:

P(E) = 50% = 0,5

P(F) = 70% = 0,7

P(G) = 30% = 0,3

Do đó, ta có: P(H) = P(E) + P(F) – P(G) = 0,5 + 0,7 – 0,3 = 0,9.

Vậy xác suất để người đó mua ít nhất một trong hai sách A và B là 0,9.

b)

Gọi $\overline{H}$ là biến cố đối của H, tức là $\overline{H}$ là biến cố “Người đó không mua cả sách A và sách B”.

Áp dụng công thức xác suất cho biến cố đối ta có:

P($\overline{H}$) = 1 – P(H) = 1 – 0,9 = 0,1.

Vậy xác suất để người đó không mua cả sách A và sách B là 0,1.

Bài 8.10 trang 75 Toán 11 Tập 2: Tại các trường trung học phổ thông của một tỉnh, thống kê cho thấy có 63% giáo viên môn Toán tham khảo bộ sách giáo khoa A, 56% giáo viên môn Toán tham khảo bộ sách giáo khoa B và 28,5% giáo viên môn Toán tham khảo cả hai bộ sách giáo khoa A và B. Tính tỉ lệ giáo viên môn Toán tại các trường trung học phổ thông của tỉnh đó không tham khảo cả hai bộ sách giáo khoa A và B.

Lời giải:

Gọi A là biến cố “Giáo viên môn Toán tham khảo bộ sách A”; B là biến cố “Giáo viên môn Toán tham khảo bộ sách B”.

Do đó, A ∩ B là biến cố “Giáo viên Toán tham khảo cả hai bộ sách A và B”;

C = A ∪ B là biến cố “Giáo viên Toán tham khảo ít nhất một trong hai bộ sách A và B”.

Biến cố đối của C là biến cố $\overline{C}$ : “Giáo viên Toán không tham khảo cả hai bộ sách giáo khoa A và B”.

Ta có:

P(A) = 63% = 0,63

P(B) = 56% = 0,56

P(AB) = 28,5% = 0,285

Áp dụng công thức cộng xác suất ta có:

P(C) = P(A ∪ B) = P(A) + P(B) – P(AB) = 0,63 + 0,56 – 0,285 = 0,905.

Áp dụng công thức xác suất cho biến cố đối ta có:

P($\overline{C}$) = 1 – P(C) = 1 – 0,905 = 0,095.

Vậy xác suất để giáo viên đó không tham khảo cả hai bộ sách giáo khoa A và B là 0,095. Tức là, tỉ lệ có 9,5%giáo viên môn Toán tại các trường trung học phổ thông của tỉnh đó không tham khảo cả hai bộ sách giáo khoa A và B.

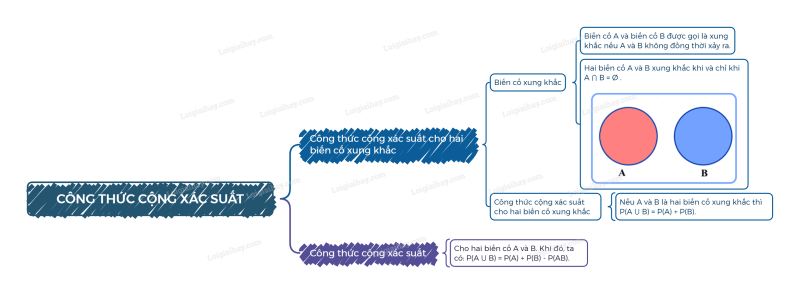
Lý thuyết Công thức cộng xác suất

1. Công thức cộng xác suất cho hai biến cố xung khắc

a) Biến cố xung khắc

Biến cố A và biến cố B được gọi là xung khắc nếu A và B không đồng thời xảy ra.

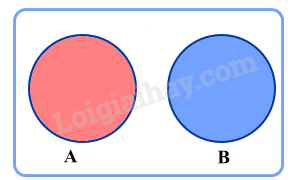
b) Công thức cộng xác suất cho hai biến cố xung khắc

Nếu A và B là hai biến cố xung khắc thì $P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)$.

2. Công thức cộng xác suất

Cho hai biến cố A và B. Khi đó, ta có:

$P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(AB\right)$.

Công thức này được gọi là công thức cộng xác suất.

Sơ đồ tư duy Công thức cộng xác suất

Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 28: Biến cố hợp, biến cố giao, biến cố độc lập

Bài 30: Công thức nhân xác suất cho hai biến cố độc lập

Bài tập cuối chương 8 trang 79

Bài 31: Định nghĩa và ý nghĩa của đạo hàm

Bài 32: Các quy tắc tính đạo hàm