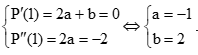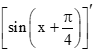Toán 11 Bài 33 (Kết nối tri thức): Đạo hàm cấp hai

Với giải bài tập Toán lớp 11 Bài 33: Đạo hàm cấp hai sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 Bài 33.

1 1,074 17/09/2024

Trang trước

Trang sau

Giải Toán 11 Bài 33: Đạo hàm cấp hai

Giải Toán 11 trang 95 Tập 2

Mở đầu trang 95 Toán 11 Tập 2: Chuyển động của một vật gắn trên con lắc lò xo (khi bỏ qua ma sát và sức cản không khí) được cho bởi phương trình sau:

x(t) = 4cos $(2 π t + \frac{π}{3})$ ,

ở đó x tính bằng centimet và thời gian t tính bằng giây. Tìm gia tốc tức thời của vật tại thời điểm t = 5 giây (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Vận tốc của vật tại thời điểm t là

v(t) = x'(t) = - $(2 π t + \frac{π}{3})$ '.4sin $(2 π t + \frac{π}{3})$ = -8 $π$ sin $(2 π t + \frac{π}{3})$ .

Gia tốc tức thời của vật tại thời điểm t là:

a(t) = v'(t) = -8 $π$ $(2 π t + \frac{π}{3})$ '.cos $(2 π t + \frac{π}{3})$ = -16 $π^{2}$ cos $(2 π t + \frac{π}{3})$ .

Tại thời điểm t = 5, gia tốc của vật là:

a(5) = $- 16 π^{2} \cos (2 π .5 + \frac{π}{3}) \approx - 79$ (cm/s²).

1. Khái niệm đạo hàm cấp hai

HĐ1 trang 95 Toán 11 Tập 2: Nhận biết đạo hàm cấp hai của một hàm số

a) Gọi g(x) là đạo hàm của hàm số y = sin $(2 x + \frac{π}{4})$ . Tìm g(x).

b) Tính đạo hàm của hàm số y = g(x).

Lời giải:

a) Ta có

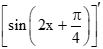
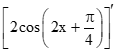
g(x) = y' = HĐ1 trang 95 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 = 2.cos $(2 x + \frac{π}{4})$ .

b) Ta có

g'(x) = HĐ1 trang 95 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 = -4sin $(2 x + \frac{π}{4})$ .

Luyện tập 1 trang 95 Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:

a) y = xe^2x;

b) y = ln(2x + 3).

Lời giải:

a) Ta có y = xe^2x

Suy ra: y' = x' . e^2x + x . (e^2x)' = e^2x + 2xe^2x.

Do đó, y'' = 2e^2x + 2(e^2x + 2xe^2x) = 2e^2x + 2e^2x + 4xe^2x = 4e^2x + 4xe^2x.

Vậy đạo hàm cấp hai của hàm số đã cho là y'' = 4e^2x + 4xe^2x.

b) Ta có y = ln(2x + 3).

y' = $\frac{(2 x + 3)^{'}}{2 x + 3} = \frac{2}{2 x + 3}$ .

y'' = ${(\frac{2}{2 x + 3})}^{'} = \frac{- 2.2}{{(2 x + 3)}^{2}} = \frac{- 4}{{(2 x + 3)}^{2}}$ .

Vậy đạo hàm cấp hai của hàm số đã cho là y'' = $\frac{- 4}{{(2 x + 3)}^{2}}$ .

2. Ý nghĩa cơ học của đạo hàm cấp hai

Giải Toán 11 trang 96 Tập 2

HĐ2 trang 96 Toán 11 Tập 2: Nhận biết ý nghĩa cơ học của đạo hàm cấp hai

Xét một chuyển động có phương trình s = 4cos2πt.

a) Tính vận tốc tức thời của chuyển động tại thời điểm t.

b) Tính gia tốc tức thời tại thời điểm t.

Lời giải:

Ta có: v(t) = s'(t) = –4.2πsin2πt = –8πsin2πt.

Vậy vận tốc tức thời của chuyển động tại thời điểm t là –8πsin2πt.

b) Gia tốc tức thời tại thời điểm t là

a(t) = v'(t) = (–8πsin2πt)' = –8π.2πcos2πt = –16π²cos2πt.

Vận dụng trang 96 Toán 11 Tập 2: Một chuyển động thẳng có phương trình $s = 2 t^{2} + \frac{1}{2} t^{4}$ (s tính bằng mét, t tính bằng giây). Tìm gia tốc của vật tại thời điểm t = 4 giây.

Lời giải:

Vận tốc tại thời điểm t là v(t) = s'(t) = 4t + 2t³.

Gia tốc tức thời của vật tại thời điểm t là a(t) = v'(t) = 4 + 6t².

Tại thời điểm t = 4 giây, gia tốc của vật là:

a(4) = 4 + 6 . 4² = 100 (m/s²).

Bài tập

Bài 9.13 trang 96 Toán 11 Tập 2: Cho hàm số f(x) = x²e^x. Tính f''(0).

Lời giải:

Với f(x) = x²e^x, ta có:

f'(x) = (x²)' . e^x + x² . (e^x)' = 2x.e^x + x².e^x.

f''(x) = (2e^x + 2x.e^x) + (2x.e^x + x².e^x) = 4xe^x + 2e^x + x²e^x.

Vậy f''(0) = 4 . 0 . e⁰ + 2 . e⁰ + 0². e⁰ = 2.

Bài 9.14 trang 96 Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:

a) y = ln(x + 1);

b) y = tan2x.

Lời giải:

a) Ta có y' = (ln(x+1))' = $\frac{{(x + 1)}^{'}}{x + 1} = \frac{1}{x + 1}$

$\Rightarrow {y^{'}}^{'} = {(\frac{1}{x + 1})}^{'} = \frac{- 1}{{(x + 1)}^{2}}$ .

Ta có y' = (tan2x)' = $\frac{2}{\cos^{2} 2 x}$

$\Rightarrow {y^{'}}^{'} = \frac{- 2 {(\cos^{2} 2 x)}^{'}}{\cos^{4} 2 x} = \frac{- 2.2 \cos 2 x . (\cos 2 x)^{'}}{\cos^{4} 2 x}$

$= \frac{4.2 \sin 2 x}{\cos^{3} 2 x} = \frac{8 \sin 2 x}{\cos^{3} 2 x}$ .

Bài 9.15 trang 96 Toán 11 Tập 2: Cho hàm số P(x) = ax² + bx + 3 (a, b là hằng số). Tìm a, b biết P'(1) = 0 và P''(1) = –2.

Lời giải:

Ta có:

P'(x) = 2ax + b

P''(x) = 2a

Do P'(1) = 0 và P''(1) = –2 nên ta có

Bài 9.15 trang 96 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Vậy a = – 1 và b = 2.

Bài 9.16 trang 96 Toán 11 Tập 2: Cho hàm số f(x) = $2 \sin^{2} (x + \frac{π}{4})$ . Chứng minh rằng |f''(x)| ≤ 4 với mọi x.

Lời giải:

Ta có:

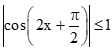
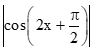
$f^{'} (x) = 2.2 \sin (x + \frac{π}{4})$ . Bài 9.16 trang 96 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

$= 4 \sin (x + \frac{π}{4}) \cos (x + \frac{π}{4}) = 2 \sin (2 x + \frac{π}{2})$

Khi đó ${f^{'}}^{'} (x) = 2. {(2 x + \frac{π}{2})}^{'} . \cos (2 x + \frac{π}{2}) = 4 \cos (2 x + \frac{π}{2})$ .

Vì Bài 9.16 trang 96 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 với mọi x nên 4 $\leq$ 4 với mọi x.

Vậy |f''(x)| ≤ 4 với mọi x.

Bài 9.17 trang 96 Toán 11 Tập 2: Phương trình chuyển động của một hạt được cho bởi s(t) = 10 + 0,5sin $(2 π t + \frac{π}{5})$ , trong đó s tính bằng centimet và t tính bằng giây. Tính gia tốc của hạt tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

Vận tốc tại thời điểm t là:

v(t) = s'(t) = 0,5.2πcos $(2 π t + \frac{π}{5})$ = πcos $(2 π t + \frac{π}{5})$ .

Gia tốc tức thời của vật tại thời điểm t là:

a(t) = v'(t) = –π.2πsin $(2 π t + \frac{π}{5})$ = –2π²sin $(2 π t + \frac{π}{5})$ .

Tại thời điểm t = 5 giây, gia tốc của vật là:

a(5) = –2π²sin $(2 π t + \frac{π}{5})$ ≈ –11,6 (cm/s²).

Lý thuyết Đạo hàm cấp hai

1. Khái niệm đạo hàm cấp hai

Giả sử hàm số y = f(x) có đạo hàm tại mỗi điểm $x \in (a; b)$ . Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x, kí hiệu là y” hoặc f”(x).

$f^{″} (x) = {(f^{'} (x))}^{'}$ .

2. Ý nghĩa cơ học của đạo hàm cấp hai

Một chuyển động có phương trình s = f(t) thì đạo hàm cấp hai (nếu có) của hàm số f(t) là gia tốc tức thời của chuyển động. Ta có:

$a (t) = f^{″} (t)$ .

Sơ đồ tư duy Đạo hàm cấp hai

Lý thuyết Đạo hàm cấp hai (Kết nối tri thức 2024) hay, chi tiết | Toán lớp 11 (ảnh 1)

Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 31: Định nghĩa và ý nghĩa của đạo hàm

Bài 32: Các quy tắc tính đạo hàm

Bài tập cuối chương 9 trang 97

Một vài mô hình toán học sử dụng hàm số mũ và hàm số lôgarit

Hoạt động thực hành trải nghiệm Hình học

1 1,074 17/09/2024

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3