Toán 11 Bài 28 (Kết nối tri thức): Biến cố hợp, biến cố giao, biến cố độc lập

Giải Toán 11 Bài 28: Biến cố hợp, biến cố giao, biến cố độc lập

Giải Toán 11 trang 66 Tập 2

Mở đầu trang 66 Toán 11 Tập 2: Trong một cuộc khảo sát về mức sống của người Hà Nội, người khảo sát chọn ngẫu nhiên một gia đình ở Hà Nội. Xét các biến cố sau:

M: “Gia đình có tivi”;

N: “Gia đình có máy vi tính”;

E: “Gia đình có tivi hoặc máy vi tính”;

F: “Gia đình có cả tivi và máy vi tính”;

G: “Gia đình có tivi hoặc máy vi tính nhưng không có cả hai thiết bị trên”;

H: “Gia đình không có cả tivi và máy vi tính”.

Các biến cố trên rõ ràng có mối liên hệ với nhau. Chúng ta có thể mô tả các mối liên hệ đó một cách cô đọng, súc tích bằng các khái niệm và các kí hiệu toán học được không

Lời giải:

Sau bài học, chúng ta có thể mô tả các mối liên hệ đó một cách cô đọng, súc tích bằng các khái niệm và các kí hiệu toán học.

Gọi A là biến cố “Gia đình có tivi”; B là biến cố “Gia đình có máy vi tính”;

Với $\overline{A}$ là biến cố đối của A, $\overline{B}$ là biến cố đối của B.

Biến cố “Gia đình có tivi hoặc máy vi tính” là biến cố A ∪ B.

Biến cố “Gia đình có cả tivi và máy vi tính” là biến cố A ∩ B.

Biến cố “Gia đình có tivi hoặc máy vi tính nhưng không có cả hai thiết bị trên” là biến cố (A \ B) ∪ (B \ A).

Biến cố “Gia đình không có cả tivi và máy vi tính” là biến cố $\overline{A}$ ∩$\overline{B}$.

1. Biến cố hợp

Giải Toán 11 trang 68 Tập 2

Luyện tập 1 trang 68 Toán 11 Tập 2: Một tổ trong lớp 11B có 4 học sinh nữ là Hương, Hồng, Dung, Phương và 5 học sinh nam là Sơn, Tùng, Hoàng, Tiến, Hải. Trong giờ học, các giáo viên chọn ngẫu nhiên một học sinh trong tổ đó lên bảng để kiểm tra bài.

Xét các biến cố sau:

H: “Học sinh đó là một bạn nữ”;

K: “Học sinh đó có tên bắt đầu là chữ cái H”.

a) Mô tả không gian mẫu.

b) Nêu nội dung của biến cố hợp M = H ∪ K. Mỗi biến cố H, K, M là tập con nào của không gian mẫu ?

Lời giải:

a) Không gian mẫu:

Ω = {Hương; Hồng; Dung; Phương; Sơn; Tùng; Hoàng; Tiến; Hải}.

b)

M = H ∪K là biến cố: “Học sinh đó là một bạn nữ hoặc có tên bắt đầu là chữ cái H.”

Ta có:

H = {Hương; Hồng; Dung; Phương}.

K = {Hương; Hồng; Hoàng; Hải}.

Vậy M = H ∪ K = {Hương; Hồng; Dung; Phương; Hoàng; Hải}.

2. Biến cố giao

HĐ2 trang 68 Toán 11 Tập 2: Trở lại tình huống trong HĐ1. Xét biến cố D: “Học sinh đó được điểm giỏi môn Ngữ văn và điểm giỏi môn Toán”.

a) Hỏi D là tập con nào của không gian mẫu?

b) Tìm A ∩ B.

Lời giải:

a) D = {Cường; Trang}.

b) A ∩ B = {Cường; Trang}.

Giải Toán 11 trang 69 Tập 2

Luyện tập 2 trang 69 Toán 11 Tập 2: Một hộp đựng 25 tấm thẻ cùng loại được đánh số từ 1 đến 25. Rút ngẫu nhiên một tấm thẻ trong hộp. Xét các biến cố P: “Số ghi trên tấm thẻ là số chia hết cho 4”; Q: “Số ghi trên tấm thẻ là số chia hết cho 6”.

a) Mô tả không gian mẫu.

b) Nội dung của biến cố giao S = PQ là gì? Mỗi biến cố P, Q, S là tập con nào của không gian mẫu?

Lời giải:

a) Không gian mẫu:

Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25}.

b)

Biến cố S = PQ là biến cố “Số ghi trên tấm thẻ là số vừa chia hết cho 4 vừa chia hết cho 6”.

Ta có:

P = {4; 8; 12; 16; 20; 24}.

Q = {6; 12; 18; 24}.

Vậy S = P ∩ Q = {12; 24}.

Vận dụng trang 69 Toán 11 Tập 2: Trở lại tình huống mở đầu. Sử dụng khái niệm biến cố hợp, biến cố giao, biến cố đối, ta biểu diễn biến cố G, H theo các biến cố M và N như sau:

Biến cố G xảy ra khi và chỉ khi hoặc gia đình đó có ti vi và không có máy vi tính hoặc gia đình đó không có ti vi và có máy vi tính. Vậy G = M$\overline{N}$$\cup$$\overline{M}$N.

Biến cố H xảy ra khi và chỉ khi gia đình đó không có cả ti vi và máy vi tính. Vậy H = $\overline{M}$$\overline{N}$ .

Hãy biểu diễn mỗi biến cố E, F theo các biến cố M và N.

Lời giải:

Biến cố E xảy ra khi và chỉ khi hoặc gia đình đó có ti vi hoặc gia đình đó có máy vi tính. Vậy E = M∪ N.

Biến cố F xảy ra khi và chỉ khi gia đình đó vừa có ti vi vừa có máy vi tính.

Vậy F = MN.

3. Biến cố độc lập

HĐ3 trang 69 Toán 11 Tập 2: Hai bạn Minh và Sơn, mỗi người gieo đồng thời một con xúc xắc cân đối, đồng chất. Xét hai biến cố sau:

A: “Số chấm xuất hiện trên con xúc xắc bạn Minh gieo là số chẵn”;

B: “Số chấm xuất hiện trên con xúc xắc bạn Sơn gieo là số chia hết cho 3”.

Việc xảy ra hay không xảy ra biến cố A có ảnh hưởng tới xác suất xảy ra của biến cố B không ? Việc xảy ra hay không xảy ra biến cố B có ảnh hưởng tới xác suất xảy ra của biến cố A hay không ?

Lời giải:

Vì biến cố A liên quan đến số chấm xuất hiện trên con xúc xắc bạn Minh gieo, còn biến cố B liên quan đến số chấm xuất hiện trên con xúc xắc bạn Sơn gieo, mà hai bạn gieo đồng thời nên việc xảy ra hay không xảy ra biến cố A không ảnh hưởng tới xác suất xảy ra của biến cố B. Hay ngược lại việc xảy ra hay không xảy ra biến cố B không ảnh hưởng tới xác suất xảy ra của biến cố A.

Giải Toán 11 trang 70 Tập 2

Luyện tập 3 trang 70 Toán 11 Tập 2: Trở lại tình huống trong HĐ3. Xét hai biến cố sau:

E: “Số chấm xuất hiện trên con xúc xắc bạn Minh gieo là số nguyên tố”;

B: “Số chấm xuất hiện trên con xúc xắc bạn Sơn gieo là số chia hết cho 3”.

Hai biến cố E và B độc lập hay không độc lập

Lời giải:

Nếu E xảy ra, tức là số chấm xuất hiện trên con xúc xắc bạn Minh gieo là số nguyên tố. Vì Minh và Sơn mỗi bạn có một con xúc xắc và gieo xúc xắc đồng thời nên số chấm xuất hiện trên con xúc xắc bạn Sơn gieo có thể là một trong các số: 1; 2; 3; 4; 5; 6, trong đó, các số chia hết cho 3 là: 3; 6. Vậy P(B) = $\frac{2}{6}$ = $\frac{1}{3}$.

Nếu E không xảy ra, tức là số chấm xuất hiện trên con xúc xắc bạn Minh gieo không là số nguyên tố. Vì Minh và Sơn mỗi bạn có một con xúc xắc và gieo xúc xắc đồng thời nên số chấm xuất hiện trên con xúc xắc bạn Sơn gieo có thể là một trong các số: 1; 2; 3; 4; 5; 6, trong đó, các số chia hết cho 3 là: 3; 6. Vậy P(B) = $\frac{2}{6}$ = $\frac{1}{3}$.

Như vậy, xác suất xảy ra của biến cố B không thay đổi bởi việc xảy ra hay không xảy ra của biến cố E.

Vì mỗi bạn một con xúc xắc nên P(E) = $\frac{3}{6}=\frac{1}{2}$ dù biến cố B có xảy ra hay không xảy ra.

Vậy A và B độc lập.

Bài tập

Giải Toán 11 trang 71 Tập 2

Bài 8.1 trang 71 Toán 11 Tập 2: Một hộp đựng 15 tấm thẻ cùng loại được đánh số từ 1 đến 15. Rút ngẫu nhiên một tấm thẻ và quan sát số ghi trên thẻ. Gọi A là biến cố “Số ghi trên tấm thẻ nhỏ hơn 7”; B là biến cố “Số ghi trên tấm thẻ là số nguyên tố”.

a) Mô tả không gian mẫu.

b) Mỗi biến cố A∪ B và AB là tập con nào của không gian mẫu ?

Lời giải:

a) Không gian mẫu: $\Omega$ = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15}.

b)

Ta có:

A = {1; 2; 3; 4; 5; 6}.

B = {2; 3; 5; 7; 11; 13}.

Vậy A∪ B = {1; 2; 3; 4; 5; 6; 7; 11; 13} và AB = A ∩ B = {2; 3; 5}.

Bài 8.2 trang 71 Toán 11 Tập 2: Gieo hai con xúc xắc cân đối, đồng chất. Xét các biến cố sau:

E: “Số chấm xuất hiện trên hai con xúc xắc đều là số chẵn”;

F: “Số chấm xuất hiện trên hai con xúc xắc khác tính chẵn lẻ”;

K: “Tích số chấm xuất hiện trên hai con xúc xắc là số chẵn”.

Chứng minh K là biến cố hợp của E và F.

Lời giải:

Không gian mẫu: $\Omega$ = {(x; y) | 1 ≤ x ≤ 6; 1 ≤ y ≤ 6}.

Ta có:

E = {(2; 2); (2; 4); (2; 6); (4; 2); (4; 4); (4; 6); (6; 2); (6; 4); (6; 6)}.

F = {(1; 2); (1; 4); (1; 6); (2; 1); (2; 3); (2; 5); (3; 2); (3; 4); (3; 6); (4; 1); (4; 3); (4; 5); (5; 2); (5; 4); (5; 6); (6; 1); (6; 3); (6; 5)}.

Suy ra: E ∪ F = {(2; 2); (2; 4); (2; 6); (4; 2); (4; 4); (4; 6); (6; 2); (6; 4); (6; 6); (1; 2); (1; 4); (1; 6); (2; 1); (2; 3); (2; 5); (3; 2); (3; 4); (3; 6); (4; 1); (4; 3); (4; 5); (5; 2); (5; 4); (5; 6); (6; 1); (6; 3); (6; 5)}.

Mặt khác:

K = {(2; 2); (2; 4); (2; 6); (4; 2); (4; 4); (4; 6); (6; 2); (6; 4); (6; 6); (1; 2); (1; 4); (1; 6); (2; 1); (2; 3); (2; 5); (3; 2); (3; 4); (3; 6); (4; 1); (4; 3); (4; 5); (5; 2); (5; 4); (5; 6); (6; 1); (6; 3); (6; 5)}

Vậy K = E ∪ F (điều cần phải chứng minh).

Ngoài ra, ta có thể chứng minh như sau:

Nếu E hoặc F xảy ra thì K xảy ra. Ngược lại, nếu K xảy ra thì trong số chấm xuất hiện trên hai con xúc xắc phải có ít nhất một số chẵn: nếu cả hai số đều chẵn thì E xảy ra; nếu một số chẵn, một số lẻ thì F xảy ra. Nghĩa là nếu K xảy ra thì hoặc E xảy ra hoặc F xảy ra. Vậy K là biến cố hợp của E và F.

Bài 8.3 trang 71 Toán 11 Tập 2: Chọn ngẫu nhiên một học sinh trong trường em. Xét hai biến cố sau:

P: “Học sinh đó bị cận thị”;

Q: “Học sinh đó học giỏi môn Toán”.

Nêu nội dung của các biến cố P∪ Q, PQ và $\overline{P}$$\overline{Q}$ .

Lời giải:

- Biến cố P∪ Q là biến cố “Học sinh đó hoặc bị cận thị hoặc học giỏi môn Toán”.

- Biến cố PQ là biến cố “Học sinh đó vừa bị cận thị vừa học giỏi môn Toán”.

- Biến cố $\overline{P}$ là biến cố “Học sinh đó không bị cận thị”; biến cố $\overline{Q}$ là biến cố “Học sinh đó không học giỏi môn Toán”. Vậy biến cố $\overline{P}$$\overline{Q}$ là biến cố “Học sinh đó vừa không bị cận thị vừa không học giỏi môn Toán”.

Bài 8.4 trang 71 Toán 11 Tập 2: Có hai chuồng nuôi thỏ. Chuồng I có 5 con thỏ đen và 10 con thỏ trắng. Chuồng II có 3 con thỏ trắng và 7 con thỏ đen. Từ mỗi chuồng bắt ngẫu nhiên ra một con thỏ. Xét hai biến cố sau:

A: “Bắt được con thỏ trắng từ chuồng I”;

B: “Bắt được con thỏ đen từ chuồng II”.

Chứng tỏ rằng hai biến cố A và B độc lập.

Lời giải:

Nếu biến cố A xảy ra, tức là bắt được con thỏ trắng từ chuồng I, vì chuồng II chưa bị bắt thỏ nên trong chuồng II vẫn có 3 con thỏ trắng và 7 con thỏ đen. Vậy P(B) = $\frac{7}{10}$ .

Nếu biến cố A không xảy ra, tức là bắt được con thỏ đen từ chuồng I, vì chuồng II chưa bị bắt thỏ nên trong chuồng II vẫn có 3 con thỏ trắng và 7 con thỏ đen. Vậy P(B) = $\frac{7}{10}$ .

Như vậy, xác suất của biến cố B không phụ thuộc vào việc xảy ra hay không xảy ra của biến cố A.

Và dù B xảy ra hay không xảy ra, ta cũng luôn có P(A) = $\frac{10}{15}=\frac{2}{3}$ .

Vậy A và B là hai biến cố độc lập.

Bài 8.5 trang 71 Toán 11 Tập 2: Có hai chuồng nuôi gà. Chuồng I có 9 con gà mái và 3 con gà trống. Chuồng II có 3 con gà mái và 6 con gà trống. Bắt ngẫu nhiên một con gà của chuồng I để đem bán rồi dồn các con gà còn lại của chuồng I vào chuồng II. Sau đó bắt ngẫu nhiên một con gà của chuồng II. Xét hai biến cố sau:

E: “Bắt được con gà trống từ chuồng I”;

F: “Bắt được con gà mái từ chuồng II”.

Chứng tỏ rằng hai biến cố E và F không độc lập.

Lời giải:

Nếu biến cố E xảy ra, tức là bắt được con gà trống từ chuồng I, vì sau khi bắt dồn các con gà còn lại của chuồng I vào chuồng II nên trong chuồng II có 12 con gà mái và 8 con gà trống. Vậy P(F) = $\frac{12}{20}=\frac{3}{5}$ .

Nếu biến cố E không xảy ra, tức là bắt được con gà mái từ chuồng I, vì sau khi bắt dồn các con gà còn lại của chuồng I vào chuồng II nên trong chuồng II có 11 con gà mái và 9 con gà trống. Vậy P(F) = $\frac{11}{20}$ .

Như vậy, xác suất của biến cố F thay đổi phụ thuộc vào việc xảy ra hay không xảy ra của biến cố E. Vậy E và F không độc lập.

Lý thuyết Biến cố hợp, biến cố giao, biến cố độc lập

1. Biến cố hợp

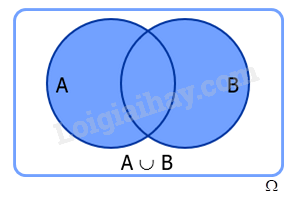
Cho A và B là hai biến cố. Biến cố: “A hoặc B xảy ra” được gọi là biến cố hợp của A và B, kí hiệu là $A\cup B$.

Biến cố hợp của A và B là tập con $A\cup B$ của không gian mẫu $\mathrm{\Omega }$.

CÓ C2 MÁT LÀNH, SAO PHẢI GẮT?

facebook.com

Tìm hiểu thêm

2. Biến cố giao

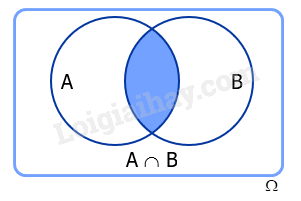
Cho A và B là hai biến cố. Biến cố: “Cả A và B đều xảy ra” được gọi là biến cố giao của A và B, kí hiệu là AB.

Biến cố giao của A và B là tập con $A\cap B$ của không gian mẫu $\mathrm{\Omega }$.

CÓ C2 MÁT LÀNH, SAO PHẢI GẮT?

facebook.com

Tìm hiểu thêm

3. Biến cố độc lập

Cặp biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia.

Chú ý: Nếu cặp biến cố A và B độc lập thì các cặp biến cố: A và $\overline{B}$; $\overline{A}$ và B; $\overline{A}$ và $\overline{B}$ cũng độc lập.

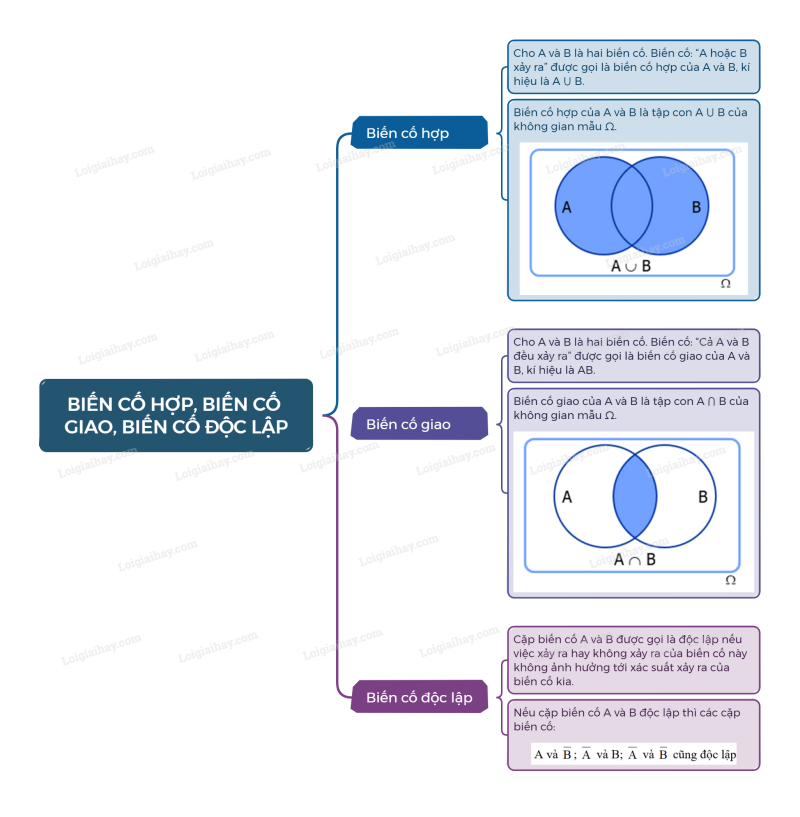
Sơ đồ tư duy Biến cố hợp, biến cố giao, biến cố độc lập

Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 7 trang 64

Bài 29: Công thức cộng xác suất

Bài 30: Công thức nhân xác suất cho hai biến cố độc lập

Bài tập cuối chương 8 trang 79

Bài 31: Định nghĩa và ý nghĩa của đạo hàm