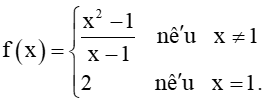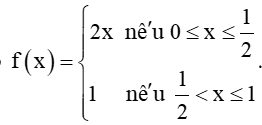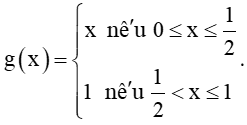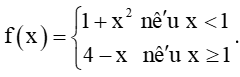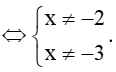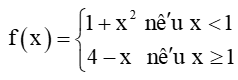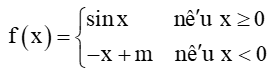Toán 11 Bài 17 (Kết nối tri thức): Hàm số liên tục

Giải Toán 11 Bài 17: Hàm số liên tục

Bài giảng Toán 11 Bài 17: Hàm số liên tục

Giải Toán 11 trang 119

Mở đầu trang 119 Toán 11 Tập 1: Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.

Lời giải:

Áp dụng định lí: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a) f(b) < 0 thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0.

1. Hàm số liên tục tại một điểm

HĐ1 trang 119 Toán 11 Tập 1: Nhận biết tính liên tục của hàm số tại một điểm

Cho hàm số

Tìm giới hạn $\underset{x\to 1}{\lim }f\left(x\right)$ và so sánh giá trị này với f(1).

Lời giải:

Ta có: f(1) = 2.

$\underset{x\to 1}{\lim }f\left(x\right)$$=\underset{x\to 1}{\lim }\frac{x^2-1}{x-1}=\underset{x\to 1}{\lim }\frac{\left(x-1\right)\left(x+1\right)}{x-1}$$=\underset{x\to 1}{\lim }\left(x+1\right)=1+1=2$.

Vậy $\underset{x\to 1}{\lim }f\left(x\right)$ = f(1).

Giải Toán 11 trang 120

Luyện tập 1 trang 120 Toán 11 Tập 1: Xét tính liên tục của hàm số 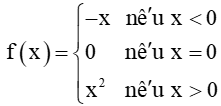tại điểm x₀ = 0.

Lời giải:

Hàm số f(x) xác định trên ℝ, do đó x₀ = 0 thuộc tập xác định của hàm số.

Ta có: $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }{x}^2=0^2=0$; $\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\left(-x\right)=0$.

Do đó, $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)=0$, suy ra $\underset{x\to 0}{\lim }f\left(x\right)=0$.

Lại có f(0) = 0 nên $\underset{x\to 0}{\lim }f\left(x\right)=f\left(0\right)$. Vậy hàm số f(x) liên tục tại x₀ = 0.

2. Hàm số liên tục trên một khoảng

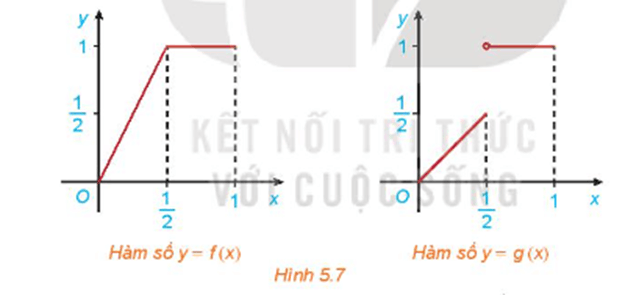
HĐ2 trang 120 Toán 11 Tập 1: Cho hai hàm số 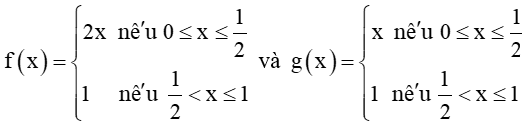với đồ thị tương ứng như Hình 5.7.

Xét tính liên tục của các hàm số f(x) và g(x) tại điểm $x=\frac{1}{2}$ và nhận xét về sự khác nhau giữa hai đồ thị.

Lời giải:

+) Hàm số

Hàm số f(x) xác định trên [0; 1], do đó $x=\frac{1}{2}$ thuộc tập xác định của hàm số.

Ta có: $\underset{x\to {\frac{1}{2}}^{+}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{+}}{\lim }1=1$; $\underset{x\to {\frac{1}{2}}^{-}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }\left(2x\right)=2\cdot \frac{1}{2}=1$.

Suy ra $\underset{x\to {\frac{1}{2}}^{+}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }f\left(x\right)=1$, do đó $\underset{x\to \frac{1}{2}}{\lim }f\left(x\right)=1$

Mà $f\left(\frac{1}{2}\right)=2\cdot \frac{1}{2}=1$ nên $\underset{x\to \frac{1}{2}}{\lim }f\left(x\right)=f\left(\frac{1}{2}\right)$.

Vậy hàm số f(x) liên tục tại $x=\frac{1}{2}$.

+) Hàm số

Hàm số g(x) liên tục trên [0; 1], do đó $x=\frac{1}{2}$ thuộc tập xác định của hàm số.

Ta có: $\underset{x\to {\frac{1}{2}}^{-}}{\lim }g\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }x=\frac{1}{2}$; $\underset{x\to {\frac{1}{2}}^{+}}{\lim }g\left(x\right)=\underset{x\to {\frac{1}{2}}^{+}}{\lim }1=1$

Suy ra $\underset{x\to {\frac{1}{2}}^{+}}{\lim }g\left(x\right)\ne \underset{x\to {\frac{1}{2}}^{-}}{\lim }g\left(x\right)$.

Vậy không tồn tại giới hạn của hàm số g(x) tại $x=\frac{1}{2}$, do đó hàm số g(x) gián đoạn tại $x=\frac{1}{2}$.

+) Quan sát Hình 5.7 ta thấy, đồ thị của hàm số y = f(x) là đường liền trên (0; 1), còn đồ thị của hàm số y = g(x) trên (0; 1) là các đoạn rời nhau.

Giải Toán 11 trang 121

Luyện tập 2 trang 121 Toán 11 Tập 1: Tìm các khoảng trên đó hàm số $f\left(x\right)=\frac{x^2+1}{x+2}$ liên tục.

Lời giải:

Biểu thức $\frac{x^2+1}{x+2}$ có nghĩa khi x + 2 ≠ 0 hay x ≠ – 2.

Do đó, tập xác định của hàm số f(x) là (–∞; – 2) ∪ (– 2; +∞).

Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 2) và (– 2; +∞).

3. Một số tính chất cơ bản

HĐ3 trang 121 Toán 11 Tập 1: Cho hai hàm số f(x) = x² và g(x) = – x + 1.

a) Xét tính liên tục của hai hàm số trên tại x = 1.

b) Tính và so sánh L với f(1) + g(1).

Lời giải:

a) Hàm số f(x) = x² và g(x) = – x + 1 là các hàm đa thức nên nó liên tục trên ℝ.

Do đó, hai hàm số f(x) và g(x) đều liên tục tại x = 1.

b) Ta có: f(x) + g(x) = x² + (– x + 1) = x² – x + 1.

Do đó, $=\underset{x\to 1}{\lim }\left(x^2-x+1\right)=1^2-1+1=1$.

Lại có, f(1) = 1² = 1; g(1) = – 1 + 1 = 0, do đó f(1) + g(1) = 1 + 0 = 1.

Vậy L = f(1) + g(1) = 1.

Bài tập

Giải Toán 11 trang 122

Bài 5.14 trang 122 Toán 11 Tập 1: Cho f(x) và g(x) là các hàm số liên tục tại x = 1. Biết f(1) = 2 và . Tính g(1).

Lời giải:

Vì hàm số f(x) liên tục tại x = 1 nên hàm số 2f(x) cũng liên tục tại x = 1.

Mà hàm số g(x) liên tục tại x = 1. Do đó, hàm số y = 2f(x) – g(x) liên tục tại x = 1.

Suy ra

Vì và f(1) = 2 nên ta có 3 = 2 . 2 – g(1) ⇔ g(1) = 1.

Vậy g(1) = 1.

Bài 5.15 trang 122 Toán 11 Tập 1: Xét tính liên tục của các hàm số sau trên tập xác định của chúng:

a) $f\left(x\right)=\frac{x}{x^2+5x+6}$;

b)

Lời giải:

a) $f\left(x\right)=\frac{x}{x^2+5x+6}$

Biểu thức $\frac{x}{x^2+5x+6}$ có nghĩa khi x² + 5x + 6 ≠ 0 ⇔ (x + 2)(x + 3) ≠ 0

Do đó, tập xác định của hàm số f(x) là ℝ \ {– 3; – 2} = (–∞; – 3) ∪ (– 3; – 2) ∪ (– 2; +∞).

Vì f(x) là hàm phân thức hữu tỉ nên nó liên tục trên tập xác định.

Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞).

b)

Tập xác định của hàm số là ℝ.

+) Nếu x < 1, thì f(x) = 1 + x².

Đây là hàm đa thức nên có tập xác định là ℝ.

Vậy nó liên tục trên (–∞; 1).

+) Nếu x > 1, thì f(x) = 4 – x.

Đây là hàm đa thức nên có tập xác định là ℝ.

Vậy nó liên tục trên (1; +∞).

+) Ta có: $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(4-x\right)=4-1=3$;

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(1+x^2\right)=1+1^2=2$.

Suy ra $\underset{x\to 1^{+}}{\lim }f\left(x\right)\ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$, do đó không tồn tại giới hạn của f(x) tại x = 1.

Khi đó, hàm số f(x) không liên tục tại x = 1.

Vậy hàm số đã cho liên tục trên các khoảng (–∞; 1), (1; +∞) và gián đoạn tại x = 1.

Bài 5.16 trang 122 Toán 11 Tập 1 :Tìm giá trị của tham số m để hàm sốliên tục trên ℝ.

Lời giải:

Tập xác định của hàm số là ℝ.

+) Nếu x > 0, thì f(x) = sin x. Do đó nó liên tục trên (0; +∞).

+) Nếu x < 0, thì f(x) = – x + m, đây là hàm đa thức nên nó liên tục trên (–∞; 0).

Khi đó, hàm số f(x) liên tục trên các khoảng (–∞; 0) và (0; +∞).

Do đó, để hàm số f(x) liên tục trên ℝ thì f(x) phải liên tục tại x = 0. Điều này xảy ra khi và chỉ khi $\underset{x\to 0}{\lim }f\left(x\right)=f\left(0\right)$$\iff \underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)=f\left(0\right)$ (1).

Lại có: $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }\sin x=0$; f(0) = sin 0 = 0; $\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\left(-x+m\right)=m$ .

Khi đó, (1) ⇔ m = 0.

Vậy m = 0 thì thỏa mãn yêu cầu bài toán.

Bài 5.17 trang 122 Toán 11 Tập 1: Một bảng giá cước taxi được cho như sau:

a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.

b) Xét tính liên tục của hàm số ở câu a.

Lời giải:

a) Gọi x (km, x > 0) là quãng đường khách di chuyển và y (đồng) là số tiền khách phải trả theo quãng đường di chuyển x.

Với x ≤ 0,5, ta có y = 10 000.

Với 0,5 < x ≤ 30, ta có: y = 10 000 + 13 500(x – 0,5) hay y = 13 500x + 3 250.

Với x > 30, ta có: y = 10 000 + 13 500 . 29,5 + 11 000(x – 30) hay y = 11 000x + 78 250.

Vậy công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển là

b) +) Với 0 < x < 0,5 thì y = 10 000 là hàm hằng nên nó liên tục trên (0; 0,5).

+) Với 0,5 < x < 30 thì y = 13500x + 3 250 là hàm đa thức nên nó liên tục trên (0,5; 30).

+) Với x > 30 thì y = 11 000x + 78 250 là hàm đa thức nên nó liên tục trên (30; +∞).

+) Ta xét tính liên tục của hàm số tại x = 0,5 và x = 30.

- Tại x = 0,5, ta có y(0,5) = 10 000;

$\underset{x\to 0,5^{-}}{\lim }y=\underset{x\to 0,5^{-}}{\lim }10000=10000$;

$\underset{x\to 0,5^{+}}{\lim }y=\underset{x\to 0,5^{+}}{\lim }\left(13500x+3250\right)$= 13 500 . 0,5 + 3 250 = 10 000.

Do đó, $\underset{x\to 0,5^{-}}{\lim }y=\underset{x\to 0,5^{+}}{\lim }y=\underset{x\to 0,5}{\lim }y=y\left(0,5\right)$ nên hàm số liên tục tại x = 0,5.

- Tại x = 30, ta có: y(30) = 13 500 . 30 + 3 250 = 408 250;

$\underset{x\to {30}^{-}}{\lim }y=\underset{x\to {30}^{-}}{\lim }\left(13500x+3250\right)$ = 13 500 . 30 + 3 250 = 408 250;

$\underset{x\to {30}^{+}}{\lim }y=\underset{x\to {30}^{+}}{\lim }\left(11000x+78250\right)$ = 11 000 . 30 + 78 250 = 408 250.

Do đó, $\underset{x\to {30}^{-}}{\lim }y=\underset{x\to {30}^{+}}{\lim }y=\underset{x\to 30}{\lim }y=y\left(30\right)$ nên hàm số liên tục tại x = 30.

Vậy hàm số ở câu a liên tục trên (0; +∞).

Lý thuyết Hàm số liên tục

1. Hàm số liên tục tại 1 điểm

Cho hàm $y=f(x)$ xác định trên khoảng $\left(a;b\right)$chứa điểm $x_0$. Hàm số $f(x)$ được gọi là liên tục tại điểm $x_0$ nếu $\underset{x\to x_0}{lim}f(x)=f(x_0)$.

Hàm số không liên tục tại $x_0$ được gọi là gián đoạn tại điểm đó.

2. Hàm số liên tục trên một khoảng

- Hàm số $y=f(x)$ được gọi là liên tục trên khoảng $\left(a;b\right)$ nếu nó liên tục tại mọi điểm thuộc khoảng này.

- Hàm số $y=f(x)$ được gọi là liên tục trên đoạn $\left[a;b\right]$nếu nó liên tục trên khoảng $\left(a;b\right)$ và $\underset{x\to a^{+}}{lim}f(x)=f(a),\underset{x\to b^{-}}{lim}f(x)=f(b)$.

*Nhận xét:

- Hàm số đa thức và hàm số $y=\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x},y=c\mathrm{o}\mathrm{s}\mathrm{x}$ liên tục trên $\mathbb{R}$.

- Các hàm số $y=\tan \mathrm{x},y=c\mathrm{o}\mathrm{t}\mathrm{x},y=\sqrt{x}$ và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.

3. Một số tính chất cơ bản

Giả sử hai hàm số $y=f(x)$ và $y=g(x)$ liên tục tại điểm $x_0$. Khi đó:

a, Các hàm số $y=f(x)\pm g(x)$ và $y=f(x).g(x)$ liên tục tại điểm $x_0$.

b, Hàm số $y=\frac{f(x)}{g(x)}$ liên tục tại điểm $x_0$nếu $g(x_0)\ne 0$.

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối chương 5

Một vài áp dụng của toán học trong tài chính