Nội dung bài viết

    Xem thêm

    Bài 5.17 trang 122 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11

    Lời giải Bài 5.17 trang 122 Toán 11 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 769 04/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 11 Bài 17: Hàm số liên tục

    Bài 5.17 trang 122 Toán 11 Tập 1: Một bảng giá cước taxi được cho như sau:

    Giá mở cửa

    (0,5 km đầu)

    Giá cước các km tiếp theo đến 30 km

    Giá cước từ km thứ 31

    10 000 đồng

    13 500 đồng

    11 000 đồng

    a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.

    b) Xét tính liên tục của hàm số ở câu a.

    Lời giải:

    a) Gọi x (km, x > 0) là quãng đường khách di chuyển và y (đồng) là số tiền khách phải trả theo quãng đường di chuyển x.

    Với x ≤ 0,5, ta có y = 10 000.

    Với 0,5 < x ≤ 30, ta có: y = 10 000 + 13 500(x – 0,5) hay y = 13 500x + 3 250.

    Với x > 30, ta có: y = 10 000 + 13 500 . 29,5 + 11 000(x – 30) hay y = 11 000x + 78 250.

    Vậy công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển là

    Bài 5.17 trang 122 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11

    b) +) Với 0 < x < 0,5 thì y = 10 000 là hàm hằng nên nó liên tục trên (0; 0,5).

    +) Với 0,5 < x < 30 thì y = 13500x + 3 250 là hàm đa thức nên nó liên tục trên (0,5; 30).

    +) Với x > 30 thì y = 11 000x + 78 250 là hàm đa thức nên nó liên tục trên (30; +∞).

    +) Ta xét tính liên tục của hàm số tại x = 0,5 và x = 30.

    - Tại x = 0,5, ta có y(0,5) = 10 000;

    limx→0,5−y=limx→0,5−10000=10000;

    limx→0,5+y=limx→0,5+13500x+3250= 13 500 . 0,5 + 3 250 = 10 000.

    Do đó, limx→0,5−y=limx→0,5+y=limx→0,5y=y0,5 nên hàm số liên tục tại x = 0,5.

    - Tại x = 30, ta có: y(30) = 13 500 . 30 + 3 250 = 408 250;

    limx→30−y=limx→30−13500x+3250 = 13 500 . 30 + 3 250 = 408 250;

    limx→30+y=limx→30+11000x+78250 = 11 000 . 30 + 78 250 = 408 250.

    Do đó, limx→30−y=limx→30+y=limx→30y=y30 nên hàm số liên tục tại x = 30.

    Vậy hàm số ở câu a liên tục trên (0; +∞).

    Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác: 

    Mở đầu trang 119 Toán 11 Tập 1: Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km...

    HĐ1 trang 119 Toán 11 Tập 1: Nhận biết tính liên tục của hàm số tại một điểm

    Cho hàm số 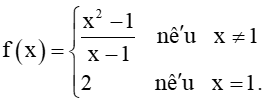HĐ1 trang 119 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11...

    Luyện tập 1 trang 120 Toán 11 Tập 1: Xét tính liên tục của hàm số

     Luyện tập 1 trang 120 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11 tại điểm x0 = 0...

    HĐ2 trang 120 Toán 11 Tập 1: 

    Cho hai hàm số HĐ2 trang 120 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11...

    Luyện tập 2 trang 121 Toán 11 Tập 1: Tìm các khoảng trên đó hàm số fx=x2+1x+2 liên tục...

    HĐ3 trang 121 Toán 11 Tập 1: Cho hai hàm số f(x) = x2 và g(x) = – x + 1. a) Xét tính liên tục của hai hàm số trên tại x = 1...

    Bài 5.14 trang 122 Toán 11 Tập 1: Cho f(x) và g(x) là các hàm số liên tục tại x = 1. Biết f(1) = 2 và Bài 5.14 trang 122 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11. Tính g(1)...

    Bài 5.15 trang 122 Toán 11 Tập 1: Xét tính liên tục của các hàm số sau trên tập xác định của chúng: a) fx=xx2+5x+6;...

    Bài 5.16 trang 122 Toán 11 Tập 1 :Tìm giá trị của tham số m để hàm sốliên tục trên ℝ.

    Bài 5.16 trang 122 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11

     

    ...

     

    Bài 5.17 trang 122 Toán 11 Tập 1: Một bảng giá cước taxi được cho như sau...

    Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác: 

    Bài 15: Giới hạn của dãy số

    Bài 16: Giới hạn của hàm số

    Bài 17: Hàm số liên tục

    Bài tập cuối chương 5

    Một vài áp dụng của toán học trong tài chính

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 769 04/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: