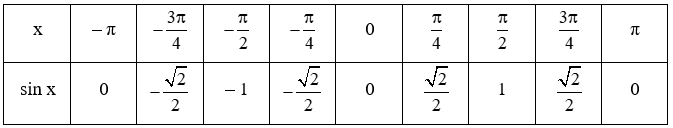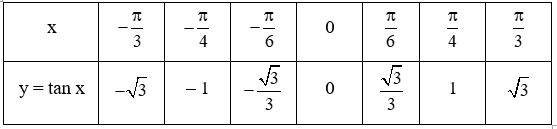Toán 11 Bài 3 (Kết nối tri thức): Hàm số lượng giác
Với giải bài tập Toán lớp 11 Bài 3: Hàm số lượng giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 Bài 3.
Giải Toán 11 Bài 3: Hàm số lượng giác
Bài giảng Toán 11 Bài 3: Hàm số lượng giác
Lời giải:
Sau bài học này, ta sẽ giải quyết được bài toán trên như sau:
Thời gian của một chu kì hô hấp đầy đủ chính là một chu kì tuần hoàn của hàm v(t) và là T = 2ππ3=6 (giây).
Ta có: 1 phút = 60 giây.
Do đó, số chu kì hô hấp trong một phút của người đó là 606=10 (chu kì).
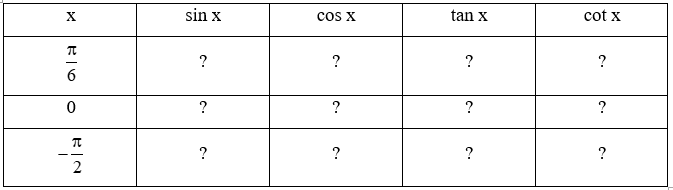
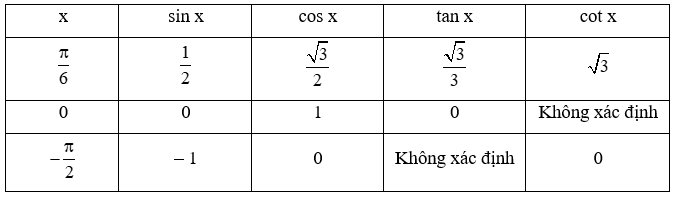
HĐ1 trang 22 Toán 11 Tập 1: Hoàn thành bảng sau:
Lời giải:
Lần lượt thay các giá trị x=π6, x=0 và x=−π2 vào sin x, cos x, tan x và cot x, ta hoàn thành được bảng như sau:
Luyện tập 1 trang 23 Toán 11 Tập 1: Tìm tập xác định của hàm số y=1sinx.
Lời giải:
Biểu thức 1sinx có nghĩa khi sin x ≠ 0, tức là x ≠ kπ (k ∈ ℤ).
Vậy tập xác định của hàm số y=1sinx là ℝ \ {kπ | k ∈ ℤ}.
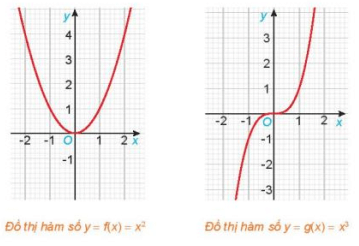
HĐ2 trang 23 Toán 11 Tập 1: Cho hai hàm số f(x) = x2 và g(x) = x3, với các đồ thị như hình dưới đây.
a) Tìm các tập xác định Df, Dg của các hàm số f(x) và g(x).
Lời giải:
a) Biểu thức x2 và x3 luôn có nghĩa với mọi x ∈ ℝ.
Vậy tập xác định của hàm số f(x) = x2 là Df = ℝ và tập xác định của hàm số g(x) = x3 là Dg = ℝ.
b) ∀ x ∈ Df, ta luôn có f(– x) = (– x)2 = x2 = f(x). Vậy f(– x) = f(x), ∀ x ∈ Df.
Từ hình vẽ ta thấy đồ thị hàm số f(x) = x2 đối xứng với nhau qua trục tung Oy.
c) ∀ x ∈ Dg, ta luôn có g(– x) = (– x)3 = – x3 = – g(x). Vậy g(– x) = – g(x), ∀ x ∈ Dg.
Từ hình vẽ ta thấy đồ thị hàm số g(x) = x3 nhận gốc tọa độ O làm tâm đối xứng.
Luyện tập 2 trang 24 Toán 11 Tập 1: Xét tính chẵn, lẻ của hàm số g(x)=1x.
Lời giải:
Biểu thức 1x có nghĩa khi x ≠ 0.
Suy ra tập xác định của hàm số g(x)=1x là D = ℝ \ {0}.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: g(– x) = 1−x=−1x = – g(x), ∀ x ∈ D.
Vậy g(x)=1x là hàm số lẻ.
HĐ3 trang 24 Toán 11 Tập 1: So sánh:
Lời giải:
a) Ta có: sin(x + 2π) = sin[π + (x + π)] = – sin(x + π) = – sin(π + x) = – (– sin x) = sin x.
Vậy sin(x + 2π) = sin x.
b) Ta có: cos(x + 2π) = cos[π + (x + π)] = – cos(x + π) = – (– cos x) = cos x.
Vậy cos(x + 2π) = cos x.
c) Ta có: tan(x + π) = tan(π + x) = tan x.
Vậy tan(x + π) = tan x.
d) Ta có: cot(x + π) = cot(π + x) = cot x.
Vậy cot(x + π) = cot x.
Lời giải:
Hàm số hằng f(x) = c (c là hằng số) có tập xác định D = ℝ.
Với T là số dương bất kì và với mọi x ∈ D, ta luôn có:
+) x + T ∈ D và x – T ∈ D;
+) f(x + T) = c = f(x) (vì f(x) là hàm số hằng nên với mọi x thì giá trị của hàm số đều có giá trị bằng c).
Vậy hàm số hằng f(x) = c (c là hằng số) là hàm số tuần hoàn với chu kì là một số dương bất kì.
Luyện tập 3 trang 25 Toán 11 Tập 1: Xét tính tuần hoàn của hàm số y = tan2x.
Lời giải:
Biểu thức tan 2x có nghĩa khi 2x≠π2+kπ, k∈ℤ⇔x≠π4+kπ2, k∈ℤ.
Suy ra hàm số y = tan 2x có tập xác định là D = ℝ\{π4+kπ2|k∈ℤ} .
Với mọi số thực x, ta có:
+) x−π2∈D, x+π2∈D ;
+) tan2(x+π2)=tan(2x+π)=tan2x .
Vậy y = tan 2x là hàm số tuần hoàn với chu kì T=π2 .
HĐ4 trang 25 Toán 11 Tập 1: Cho hàm số y = sin x.
a) Xét tính chẵn, lẻ của hàm số.
Lời giải:
a) Hàm số y = f(x) = sin x có tập xác định là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– x) = – sin x = – f(x), ∀ x ∈ D.
Vậy y = sin x là hàm số lẻ.
b) Ta có: sin 0 = 0, sinπ4=√22,sinπ2=1, sin3π4=√22 , sin π = 0.
Vì y = sin x là hàm số lẻ nên sin(−π4)=−sinπ4=−√22 , sin(−π2)=−sinπ2=−1 ,
sin(−3π4)=−sin3π4=−√22, sin(– π) = – sin π = 0.
Vậy ta hoàn thành được bảng như sau:
Luyện tập 4 trang 26 Toán 11 Tập 1: Tìm tập giá trị của hàm số y = 2sin x.
Lời giải:
Ta có: – 1 ≤ sin x ≤ 1 với mọi x ∈ ℝ.
Suy ra 2 . (– 1) ≤ 2sin x ≤ 2 . 1 hay – 2 ≤ 2sin x ≤ 2 với mọi x ∈ ℝ.
Vậy hàm số y = 2sin x có tập giá trị là [– 2; 2].
Vận dụng 1 trang 26 Toán 11 Tập 1: Xét tình huống mở đầu.
a) Giải bài toán ở tình huống mở đầu.
b) Biết rằng quá trình hít vào xảy ra khi v > 0 và quá trình thở ra xảy ra khi v < 0.
Trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm nào thì người đó hít vào? người đó thở ra?
Lời giải:
a) Thời gian của một chu kì hô hấp đầy đủ chính là một chu kì tuần hoàn của hàm v(t) và là T = 2ππ3=6 (giây).
Ta có: 1 phút = 60 giây.
Do đó, số chu kì hô hấp trong một phút của người đó là 606=10 (chu kì).
b) Ta có: v=0,85sinπt3
+) v > 0 khi 0,85sinπt3>0⇔sinπt3>0
Mà – 1 ≤ sin πt3 ≤ 1 với mọi x ∈ ℝ. Do đó, 0<sinπt3≤1 .
+) v < 0 khi 0,85sinπt3<0⇔sinπt3<0
Mà – 1 ≤ sin πt3 ≤ 1 với mọi x ∈ ℝ. Do đó, −1≤sinπt3<0.
+) Với t ∈ (0; 3) ta có 0<sinπt3≤1 .
+) Với t ∈ (3; 5] ta có −1≤sinπt3<0 .
Vậy trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm sau 0 giây đến trước 3 giây thì người đó hít vào và khoảng thời điểm sau 3 giây đến 5 giây thì người đó thở ra.
HĐ5 trang 26 Toán 11 Tập 1: Cho hàm số y = cos x.
a) Xét tính chẵn, lẻ của hàm số.
Lời giải:
a) Hàm số y = f(x) = cos x có tập xác định là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = cos (– x) = cos x = f(x), ∀ x ∈ D.
Vậy y = cos x là hàm số chẵn.
b) Ta có: cos 0 = 1, cosπ4=√22,cosπ2=0, cos3π4=−√22 , cos π = – 1.
Vì y = cos x là hàm số chẵn nên cos(−π4)=cosπ4=√22, cos(−π2)=cosπ2=0 ,
cos(−3π4)=cos3π4=−√22, cos(– π) = cos π = – 1.
Vậy ta hoàn thành được bảng như sau:
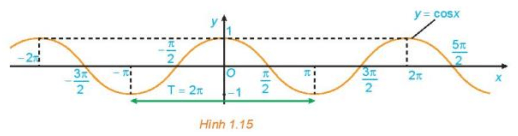
c) Quan sát Hình 1.15, ta thấy đồ thị hàm số y = cos x có:
+) Tập giá trị là [– 1; 1];
+) Đồng biến trên mỗi khoảng (−π+k2π; k2π) (do đồ thị hàm số đi lên từ trái sang phải trên mỗi khoảng này) và nghịch biến trên mỗi khoảng (k2π; π+k2π), k∈ℤ (do đồ thị hàm số đi xuống từ trái sang phải trên mỗi khoảng này).
Luyện tập 5 trang 27 Toán 11 Tập 1: Tìm tập giá trị của hàm số y = – 3cos x.
Lời giải:
Ta có: – 1 ≤ cos x ≤ 1 với mọi x ∈ ℝ.
Suy ra (– 3) . (– 1) ≥ – 3cos x ≥ (– 3) . 1 hay – 3 ≤ – 3cos x ≤ 3 với mọi x ∈ ℝ.
Vậy hàm số y = – 3cos x có tập giá trị là [– 3; 3].
Giả sử một vật dao động điều hòa theo phương trình x(t) = – 5cos 4πt (cm).
a) Hãy xác định biên độ và pha ban đầu của dao động.
Lời giải:
a) Ta có: – 5cos 4πt = 5cos(4πt + π).
Khi đó vật dao động điều hòa theo phương trình x(t) = 5cos(4πt + π) (cm) với biên độ dao động là A = 5 > 0 và pha ban đầu của dao động là φ = π.
b) Pha của dao động tại thời điểm t = 2 (giây) là ωt + φ = 4π . 2 + π = 9π.
Dao động điều hòa có chu kì là T=2πω=2π4π=12=0,5, có nghĩa là khoảng thời gian để vật thực hiện một dao động toàn phần là 0,5 giây. Do đó, trong khoảng thời gian 2 giây, vật thực hiện được 2 : 0,5 = 4 dao động toàn phần.
HĐ6 trang 28 Toán 11 Tập 1: Cho hàm số y = tan x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = tan x trên khoảng (−π2; π2) .
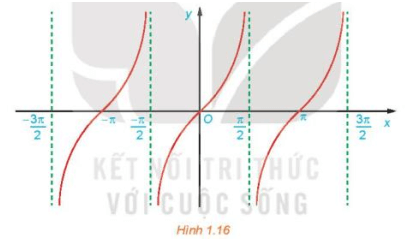
Từ đồ thị ở Hình 1.16, hãy tìm tập giá trị và các khoảng đồng biến của hàm số y = tan x.
Lời giải:
a) Hàm số y = f(x) = tan x có tập xác định là D = ℝ \ {π2+kπ|k∈ℤ} .
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = tan (– x) = – tan x = – f(x), ∀ x ∈ D.
Vậy y = tan x là hàm số lẻ.
b) Ta có: tan 0 = 0, tanπ4=1,tanπ3=√3,tanπ6=√33 .
Vì y = tan x là hàm số lẻ nên tan(−π4)=−tanπ4=−1 , tan(−π3)=−tanπ3=−√3 ,
tan(−π6)=−tanπ6=−√33.
Vậy ta hoàn thành được bảng như sau:
c) Quan sát Hình 1.16, ta thấy đồ thị hàm số y = tan x có:
+) Tập giá trị là ℝ;
+) Đồng biến trên mỗi khoảng (−π2+kπ; π2+kπ), k∈ℤ (do đồ thị hàm số đi lên từ trái sang phải trên mỗi khoảng này).
Lời giải:
Hàm số y = tan x nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ở Hình 1.16 ta suy ra trên đoạn [−π; 3π2] thì y < 0 khi x∈(−π2; 0)∪(π2; π) .
HĐ7 trang 29 Toán 11 Tập 1: Cho hàm số y = cot x.
a) Xét tính chẵn, lẻ của hàm số.
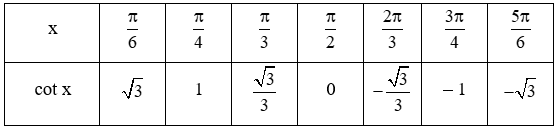
b) Hoàn thành bảng giá trị sau của hàm số y = cot x trên khoảng (0; π).
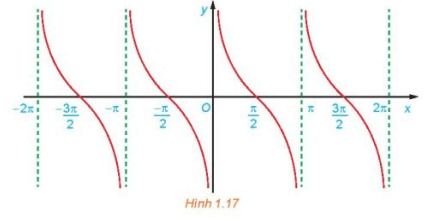
Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số y = cotx.
Lời giải:
a) Hàm số y = f(x) = cot x có tập xác định là D = ℝ \ {kπ | k ∈ ℤ}.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = cot (– x) = – cot x = – f(x), ∀ x ∈ D.
Vậy y = cot x là hàm số lẻ.
b) Ta có: cotπ6=√3,cotπ4=1, cotπ3=√33,cotπ2=0 ,
cot2π3=−√33,cot3π4=−1, cot5π6=−√3.
Vậy ta hoàn thành được bảng như sau:
c) Quan sát Hình 1.17, ta thấy đồ thị hàm số y = cot x có:
+) Tập giá trị là ℝ;
+) Nghịch biến trên mỗi khoảng (kπ; π+kπ), k∈ℤ (do đồ thị hàm số đi xuống từ trái sang phải trên mỗi khoảng này).
Lời giải:
Hàm số y = cot x nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ở Hình 1.17 ta suy ra trên đoạn [−π2; 2π] thì y > 0 khi x∈(0; π2)∪(π; 3π2) .
Bài tập
Bài 1.14 trang 30 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:
Lời giải:
a) Biểu thức 1−cosxsinx có nghĩa khi sin x ≠ 0, tức là x ≠ kπ, k ∈ ℤ.
Vậy tập xác định của hàm số y=1−cosxsinx là D = ℝ \ {kπ | k ∈ ℤ}.
b) Biểu thức √1+cosx2−cosx có nghĩa khi {1+cosx2−cosx≥02−cosx≠0.
Vì – 1 ≤ cos x ≤ 1 nên 1 + cos x ≥ 0 với mọi x ∈ ℝ và 2 – cos x ≥ 1 > 0 với mọi x ∈ ℝ.
Do đó, 2 – cos x ≠ 0 với mọi x ∈ ℝ và 1+cosx2−cosx≥0 với mọi x ∈ ℝ.
Vậy tập xác định của hàm số y=√1+cosx2−cosx là D = ℝ.
Bài 1.15 trang 30 Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau:
Lời giải:
a) Biểu thức sin 2x + tan 2x có nghĩa khi cos 2x ≠ 0 (do tan2x=sin2xcos2x ), tức là 2x≠π2+kπ,k∈ℤ⇔x≠π4+kπ2,k∈ℤ.
Suy ra tập xác định của hàm số y = f(x) = sin 2x + tan 2x là D=ℝ\{π4+kπ2|k∈ℤ} .
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– 2x) + tan (– 2x) = – sin 2x – tan 2x = – (sin 2x + tan 2x) = – f(x), ∀ x ∈ D.
Vậy y = sin 2x + tan 2x là hàm số lẻ.
b) Tập xác định của hàm số y = f(x) = cos x + sin2 x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = cos (– x) + sin2 (– x) = cos x + (– sin x)2 = cos x + sin2 x = f(x), ∀ x ∈ D.
Vậy y = cos x + sin2 x là hàm số chẵn.
c) Tập xác định của hàm số y = f(x) = sin x cos 2x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– x) . cos (– 2x) = – sin x . cos 2x = – f(x), ∀ x ∈ D.
Vậy y = sin x cos 2x là hàm số lẻ.
d) Tập xác định của hàm số y = f(x) = sin x + cos x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– x) + cos (– x) = – sin x + cos x ≠ – f(x).
Vậy y = sin x + cos x là hàm số không chẵn, không lẻ.
Bài 1.16 trang 30 Toán 11 Tập 1: Tìm tập giá trị của các hàm số sau:
Lời giải:
a) Ta có: −1≤sin(x−π4)≤1 với mọi x ∈ ℝ
⇔−2≤2sin(x−π4)≤2 với mọi x ∈ ℝ
⇔−2−1≤2sin(x−π4)−1≤2−1 với mọi x ∈ ℝ
⇔−3≤2sin(x−π4)−1≤1 với mọi x ∈ ℝ
⇔ – 3 ≤ y ≤ 1 với mọi x ∈ ℝ.
Vậy tập giá trị của hàm số y = 2sin(x−π4)−1 là [– 3; 1].
b) Vì – 1 ≤ cos x ≤ 1 với mọi x ∈ ℝ nên 0 ≤ 1 + cos x ≤ 2 với mọi x ∈ ℝ.
Do đó, 0≤√1+cosx≤√2 với mọi x ∈ ℝ.
Suy ra −2≤√1+cosx−2≤√2−2 với mọi x ∈ ℝ.
Hay −2≤y≤√2−2 với mọi x ∈ ℝ.
Vậy tập giá trị của hàm số y = √1+cosx−2 là [−2; √2−2] .
Lời giải:
Ta có đồ thị của hàm số y = tan x như hình vẽ dưới đây.
Ta có tan x = 0 khi hàm số y = tan x nhận giá trị bằng 0 ứng với các điểm x mà đồ thị giao với trục hoành. Từ đồ thị ở hình trên ta suy ra y = 0 hay tan x = 0 khi x = kπ, k ∈ ℤ.
b) Tìm chiều cao của sóng, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
Lời giải:
a) Chu kì của sóng là T=2ππ10=20 (giây).
b) Chiều cao của sóng tức là chiều cao của nước đạt được trong một chu kì dao động.
Ta có: h(20) = 90cos(π10.20) = 90 (cm).
Vậy chiều cao của sóng là 90 cm.
Lý thuyết Hàm số lượng giác
1. Định nghĩa hàm số lượng giác
- Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là R.
- Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là R.
- Hàm số cho bằng công thức y=sinαcosαđược gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là R∖{π2+kπ|k∈Z}.
- Hàm số cho bằng công thức y=cosαsinαđược gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là R∖{kπ|k∈Z}.
2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
a, Hàm số chẵn, hàm số lẻ
Cho hàm số y = f(x) có tập xác định là D.
+) Hàm số f(x) được gọi là hàm số chẵn nếu ∀x∈Dthì −x∈Dvà f(−x)=f(x). Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.
+) Hàm số f(x) được gọi là hàm số lẻ nếu ∀x∈Dthì −x∈Dvà f(−x)=−f(x). Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
b, Hàm số tuần hoàn
Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T ≠0 sao cho với mọi x∈Dta có:
+) x+T∈Dvà x−T∈D
+) f(x+T)=f(x)
Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.
* Nhận xét:
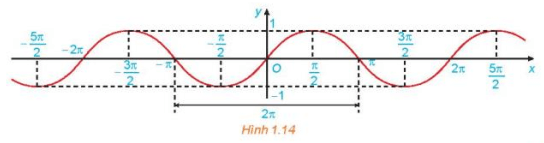
Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2π.
Các hàm số y = tanx, y=cotx tuần hoàn chu kì π.
3. Đồ thị và tính chất của hàm số y = sinx
- Tập xác định là R.
- Tập giá trị là [-1;1].
- Là hàm số lẻ và tuần hoàn chu kì 2π.
- Đồng biến trên mỗi khoảng (−π2+k2π;π2+k2π) và nghịch biến trên mỗi khoảng (π2+k2π;3π2+k2π).
- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
4. Đồ thị và tính chất của hàm số y = cosx
Tập xác định là R.
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2π.
Đồng biến trên mỗi khoảng (−π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π;π+k2π).
Có đồ thị là một đường hình sin đối xứng qua trục tung.
5. Đồ thị và tính chất của hàm số y = tanx
Tập xác định là R∖{π2+kπ|k∈Z}.
Tập giá trị là R.
Là hàm số lẻ và tuần hoàn chu kì π.
Đồng biến trên mỗi khoảng (−π2+kπ;π2+kπ), k∈Z.
Có đồ thị đối xứng qua gốc tọa độ.
6. Đồ thị và tính chất của hàm số y = cotx
Tập xác định là R∖{kπ|k∈Z}.
Tập giá trị là R.
Là hàm số lẻ và tuần hoàn chu kì π.
Đồng biến trên mỗi khoảng (kπ;π+kπ), k∈Z.
Có đồ thị đối xứng qua gốc tọa độ.
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Bài 1: Giá trị lượng giác của góc lượng giác
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức