Giải Toán 11 trang 32 Tập 1 Kết nối tri thức

Với giải bài tập Toán 11 trang 32 Tập 1 trong Bài 4: Phương trình lượng giác cơ bản sách Kết nối tri thức Tập 1 hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 32 Tập 1.

1 254 22/03/2023

Trang trước

Trang sau

Giải Toán 11 trang 32 Tập 1

Luyện tập 1 trang 32 Toán 11 Tập 1: Xét sự tương đương của hai phương trình sau:

$\frac{x - 1}{x + 1} = 0$ và x² – 1 = 0.

Lời giải:

+) Ta có: $\frac{x - 1}{x + 1} = 0$ , điều kiện x ≠ – 1.

Khi đó, $\frac{x - 1}{x + 1} = 0$ khi x – 1 = 0 hay x = 1 (thỏa mãn).

Vậy tập nghiệm của phương trình $\frac{x - 1}{x + 1} = 0$ là S₁ = {1}.

+) Phương trình x² – 1 = 0 được viết lại thành (x – 1)(x + 1) = 0, từ đó ta tìm được x = 1 hoặc x = – 1, do đó tập nghiệm của phương trình x² – 1 = 0 là S₂ = {– 1; 1}.

+) Nhận thấy S₁ ≠ S₂, vậy hai phương trình đã cho không tương đương.

HĐ2 trang 32 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình sin x = $\frac{1}{2}$

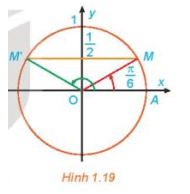
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).

b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a) Từ Hình 1.19, nhận thấy hai điểm M, M' lần lượt biểu diễn các góc $\frac{π}{6}$ và $π - \frac{π}{6} = \frac{5 π}{6}$ , lại có tung độ của điểm M và M' đều bằng $\frac{1}{2}$ nên theo định nghĩa giá trị lượng giác, ta có $\sin \frac{π}{6} = \frac{1}{2}$ và $\sin \frac{5 π}{6} = \frac{1}{2}$ .

Vậy trong nửa khoảng [0; 2π), phương trình $\sin x = \frac{1}{2}$ có hai nghiệm là $x = \frac{π}{6}$ , $x = \frac{5 π}{6}$ .

b) Vì hàm số sin có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là $x = \frac{π}{6} + k 2 π, k \in ℤ$ và $x = \frac{5 π}{6} + k 2 π, k \in ℤ$ .

Xem thêm lời giải bài tập Toán 11 sách Kết nối tri thức hay, chi tiết khác:

Giải Toán 11 trang 31 Tập 1

Giải Toán 11 trang 32 Tập 1

Giải Toán 11 trang 34 Tập 1

Giải Toán 11 trang 35 Tập 1

Giải Toán 11 trang 36 Tập 1

Giải Toán 11 trang 37 Tập 1

Giải Toán 11 trang 38 Tập 1

Giải Toán 11 trang 39 Tập 1

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Mở đầu trang 31 Toán 11 Tập 1: Một quả đạn pháo được bán ra khỏi nòng pháo với vận tốc ban đầu có độ lớn v0 không đổi. Tìm góc bắn α để quả đạn pháo bay xa nhất...

HĐ1 trang 31 Toán 11 Tập 1: Nhận biết khái niệm hai phương trình tương đương Cho hai phương trình 2x – 4 = 0 và (x – 2)(x² + 1) = 0...

Luyện tập 1 trang 32 Toán 11 Tập 1: Xét sự tương đương của hai phương trình sau:

$\frac{x - 1}{x + 1} = 0$ và x² – 1 = 0...

HĐ2 trang 32 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình sin x = $\frac{1}{2}$ ...

Luyện tập 2 trang 34 Toán 11 Tập 1: Giải các phương trình sau: a) $\sin x = \frac{\sqrt{2}}{2}$ ; b) sin 3x = – sin 5x...

HĐ3 trang 34 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cos x = $- \frac{1}{2}$ ...

Luyện tập 3 trang 35 Toán 11 Tập 1: Giải các phương trình sau: a) 2cos x = $- \sqrt{2}$ ; b) cos 3x – sin 5x = 0...

Vận dụng trang 35 Toán 11 Tập 1: Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần...

HĐ4 trang 36 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình tan x = 1 a) Quan sát Hình 1.24, hãy cho biết đường thẳng y = 1 cắt đồ thị hàm số y = tan x...

Luyện tập 4 trang 36 Toán 11 Tập 1: Giải các phương trình sau: a) $\sqrt{3} \tan 2 x = - 1$ ; b) tan 3x + tan 5x = 0...

HĐ5 trang 37 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cot x = – 1

a) Quan sát Hình 1.25, hãy cho biết đường thẳng y = – 1 cắt đồ thị hàm số y = cot x...

Luyện tập 5 trang 37 Toán 11 Tập 1: Giải các phương trình sau: a) cot x = 1; b) $\sqrt{3} \cot x + 1 = 0$ ...

Luyện tập 6 trang 38 Toán 11 Tập 1: Sử dụng máy tính cầm tay, tìm số đo độ và rađian của góc α, biết: a) cos α = – 0,75;...

Bài 1.19 trang 39 Toán 11 Tập 1: Giải các phương trình sau: a) $\sin x = \frac{\sqrt{3}}{2}$ ...

Bài 1.20 trang 39 Toán 11 Tập 1: Giải các phương trình sau: a) sin 2x + cos 4x = 0; b) cos 3x = – cos 7x...

Bài 1.21 trang 39 Toán 11 Tập 1: Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu v₀ = 500 m/s hợp với phương ngang một góc α...

Bài 1.22 trang 39 Toán 11 Tập 1: Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình $x = 2 \cos (5 t - \frac{π}{6})$ ...

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Bài 1: Giá trị lượng giác của góc lượng giác

Bài 2: Công thức lượng giác

Bài 3: Hàm số lượng giác

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

1 254 22/03/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: