Giải Toán 11 trang 107 Kết nối tri thức

Với giải bài tập Toán 11 trang 107 trong Bài 15: Giới hạn của dãy số sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 107.

1 289 04/06/2023

Trang trước

Trang sau

Giải Toán 11 trang 107

Luyện tập 3 trang 107 Toán 11 Tập 1: Tìm $\lim_{n \to + \infty} \frac{\sqrt{2 n^{2} + 1}}{n + 1}$ .

Lời giải:

Áp dụng các quy tắc tính giới hạn, ta được:

$\lim_{n \to + \infty} \frac{\sqrt{2 n^{2} + 1}}{n + 1}$ $= \lim_{n \to + \infty} \frac{\sqrt{n^{2} (2 + \frac{1}{n^{2}})}}{n + 1}$ $= \lim_{n \to + \infty} \frac{n \sqrt{2 + \frac{1}{n^{2}}}}{n (1 + \frac{1}{n})}$ $= \lim_{n \to + \infty} \frac{\sqrt{2 + \frac{1}{n^{2}}}}{1 + \frac{1}{n}} = \frac{\sqrt{2}}{1} = \sqrt{2}$ .

3. Tổng của cấp số nhân lùi vô hạn

HĐ4 trang 107 Toán 11 Tập 1: Làm quen với việc tính tổng vô hạn

Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau, sau đó tô màu hình vuông nhỏ góc dưới bên trái (H.5.2). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả sử quá trình trên tiếp diễn vô hạn lần. Gọi u₁, u₂, ..., u_n, ... lần lượt là độ dài cạnh của các hình vuông được tô màu.

a) Tính tổng S_n = u₁ + u₂ + ... + u_n.

b) Tìm S = $\lim_{n \to + \infty} S_{n}$ .

Lời giải:

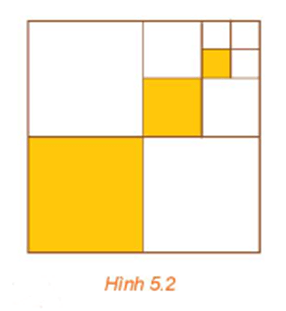
a) Ta có: u₁ là độ dài cạnh của hình vuông được tô màu tạo từ việc chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau, do đó $u_{1} = \frac{1}{2}$ .

Cứ tiếp tục như thế, ta được: $u_{2} = \frac{1}{2} u_{1}, u_{3} = \frac{1}{2} u_{2}$ ,..., $u_{n} = \frac{1}{2} u_{n - 1}$ , ...

Do vậy, độ dài cạnh của các hình vuông được tô màu lập thành một cấp số nhân với số hạng đầu $u_{1} = \frac{1}{2}$ và công bội $q = \frac{1}{2}$ .

Do đó, tổng của n số hạng đầu là

S_n = u₁ + u₂ + ... + u_n = $\frac{u_{1} (1 - q^{n})}{1 - q} = \frac{\frac{1}{2} (1 - {(\frac{1}{2})}^{n})}{1 - \frac{1}{2}}$ $= 1 - {(\frac{1}{2})}^{n}$ .

b) Ta có: S = $\lim_{n \to + \infty} S_{n}$ = $\lim_{n \to + \infty} (1 - {(\frac{1}{2})}^{n})$ $= \lim_{n \to + \infty} 1 - \lim_{n \to + \infty} {(\frac{1}{2})}^{n} = 1 - 0 = 1$ .

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Giải Toán 11 trang 105

Giải Toán 11 trang 106

Giải Toán 11 trang 107

Giải Toán 11 trang 108

Giải Toán 11 trang 109

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

HĐ1 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn là 0 Cho dãy số (u_n) với $u_{n} = \frac{{(- 1)}^{n}}{n}$ ...

Luyện tập 1 trang 105 Toán 11 Tập 1: Chứng minh rằng $\lim_{n \to + \infty} \frac{{(- 1)}^{n - 1}}{3^{n}} = 0$ ...

HĐ2 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn hữu hạn Cho dãy số (u_n) với $u_{n} = \frac{n + {(- 1)}^{n}}{n}$ . Xét dãy số (v_n) xác định bởi v_n = u_n – 1...

Luyện tập 2 trang 106 Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{{3.2}^{n} - 1}{2^{n}}$ . Chứng minh rằng $\lim_{n \to + \infty} u_{n} = 3$ ...

Vận dụng 1 trang 106 Toán 11 Tập 1: Một quả bóng cao su được thả từ độ cao 5 m xuống mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng $\frac{2}{3}$ độ cao trước đó...

HĐ3 trang 106 Toán 11 Tập 1: Hình thành quy tắc tính giới hạn. Cho hai dãy số (u_n) và (v_n) với $u_{n} = 2 + \frac{1}{n}, v_{n} = 3 - \frac{2}{n}$ ...

Luyện tập 3 trang 107 Toán 11 Tập 1: Tìm $\lim_{n \to + \infty} \frac{\sqrt{2 n^{2} + 1}}{n + 1}$ ...

HĐ4 trang 107 Toán 11 Tập 1: Làm quen với việc tính tổng vô hạn Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau...

Luyện tập 4 trang 108 Toán 11 Tập 1: Tính tổng $S = 2 + \frac{2}{7} + \frac{2}{49} + ... + \frac{2}{7^{n - 1}} + ...$

Vận dụng 2 trang 108 Toán 11 Tập 1: (Giải thích nghịch lí Zeno) Để đơn giản, ta giả sử Achilles chạy với vận tốc 100 km/h...

HĐ5 trang 108 Toán 11 Tập 1: Nhận biết giới hạn vô cực. Một loại vi khuẩn được nuôi cấy với số lượng ban đầu là 50. Sau mỗi chu kì 4 giờ, số lượng của chúng sẽ tăng gấp đôi...

Luyện tập 5 trang 109 Toán 11 Tập 1: Tính $\lim_{n \to + \infty} (n - \sqrt{n})$ ...

Bài 5.1 trang 109 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim_{n \to + \infty} \frac{n^{2} + n + 1}{2 n^{2} + 1}$ ;...

Bài 5.2 trang 109 Toán 11 Tập 1: Cho hai dãy số không âm (u_n) và (v_n) với $\lim_{n \to + \infty} u_{n} = 2$ và $\lim_{n \to + \infty} v_{n} = 3$ . Tìm các giới hạn sau...

Bài 5.3 trang 109 Toán 11 Tập 1: Tìm giới hạn của các dãy số cho bởi: a) $u_{n} = \frac{n^{2} + 1}{2 n - 1}$ ;...

Bài 5.4 trang 109 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số: a) 1,(12) = 1,121212...

Bài 5.5 trang 109 Toán 11 Tập 1: Một bệnh nhân hằng ngày phải uống một viên thuốc 150 mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%...

Bài 5.6 trang 109 Toán 11 Tập 1: Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA₁ ⊥ BC, từ A₁ kẻ A₁A₂ ⊥ AC, sau đó lại kẻ A₂A₃ ⊥ BC...

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 4

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối chương 5

Một vài áp dụng của toán học trong tài chính

1 289 04/06/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: