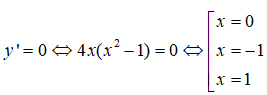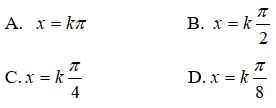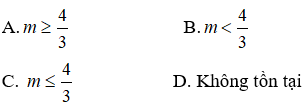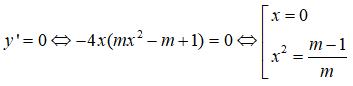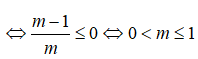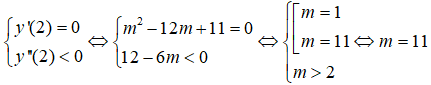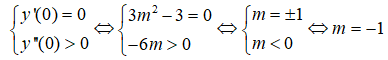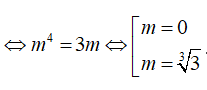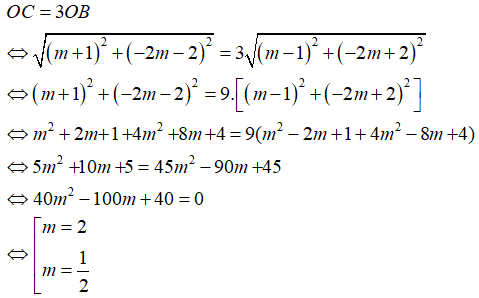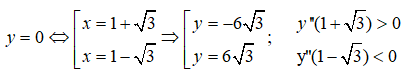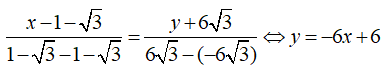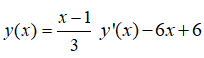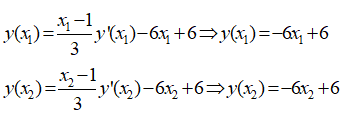TOP 40 câu Trắc nghiệm Cực trị hàm số (có đáp án 2024) - Toán 12

Trắc nghiệm Toán 12 Bài 2: Cực trị hàm số

Bài giảng Trắc nghiệm Toán 12 Bài 2: Cực trị hàm số

Câu 1. Tìm giá trị cực đại y_CĐ của hàm số y = x³ - 3x +2

A. y_CĐ = 4

B. y_CĐ = 1

C. y_CĐ = 0

D. y_CĐ = -1

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $y\text{'}=3x^2-3; y\text{'}=0$

$\iff [\begin{array}{l}x=1\Rightarrow y_{CT}=0\\ x=-1\Rightarrow y_{CĐ}=4\end{array}$

Câu 2. Cho hàm số $\frac{x^2+3}{x+1}$ . Mệnh đề nào dưới đây đúng?

A. Cực tiểu của hàm số bằng -3

B. Cực tiểu của hàm số bằng -6

C. Cực tiểu của hàm số bằng 1

D. Cực tiểu của hàm số bằng 2

Lời giải

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $y\text{'}=\frac{2x(x+1)-x^2-3}{{(x+1)}^2}$

$=\frac{x^2+2x-3}{{(x+1)}^2};$

$y\text{'}=0$$\iff [\begin{array}{l}x=1\Rightarrow y_{CT}=2\\ x=-3\Rightarrow y_{CĐ}=-6\end{array}$

Câu 3. Đồ thị của hàm số y = x³ - 3x² - 9x +1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?

A. P(1;0)

B. M(0;1)

C. N (1;-10)

D. Q(-1;10)

Lời giải

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $y\text{'}=3x^2-6x-9; y\text{'}=0$

$\iff [\begin{array}{l}x=-1\Rightarrow y=6\\ x=3\Rightarrow y=-26\end{array}$

$\Rightarrow AB: y=-8x-2.$

Câu 4. Đồ thị của hàm số y = -x³ + 3x +5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.

A. S = 9

B. S = $\frac{10}{3}$

C. S = 5

D. S = 10

Lời giải

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $y\text{'}=-3x^2+6x, y\text{'}=0$

$\iff [\begin{array}{l}x=0\Rightarrow y=5\\ x=2\Rightarrow y=9\end{array}$

$\Rightarrow A(0;5), B(2;9)$

Ta có:

$S_{OAB}=\frac{1}{2}d(B,Oy).OA$

$=\frac{1}{2}.2.5=5$

Câu 5. Cực đại (giá trị cực đại) của hàm số $y=-x^4+2x^2-2$ bằng

A. 1

B. -1

C. -2

D. 0

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $y\text{'}=-4x^3+4x; y\text{'}=0$

$\iff [\begin{array}{l}x=0\Rightarrow y_{CT}=2\\ x=\pm 1\Rightarrow y_{CĐ}=-1\end{array}$

Câu 6. Cực tiểu (giá trị cực tiểu) của hàm số $y=-\frac{1}{4}{x}^4+8x^2-3$ bằng:

A. -4

B. 4

C. -3

D. 0

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $y\text{'}=-x^3+16x; y\text{'}=0$

$\iff [\begin{array}{l}x=0\Rightarrow y_{CT}=-3\\ x=\pm 4\Rightarrow y_{CĐ}=61\end{array}$

Câu 7. Số điểm cực trị của hàm số y = x³+x²+3x-1 là

A. 1

B. 0

C. 2

D. 3

Lời giải

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có y' = 3x²+2x+3>0 không có cực trị.

Câu 8. Tìm điểm cực tiểu của đồ thị hàm số y = x³ -3x² -1?

A. (0;-2)

B. (0;1)

C. (5;-2)

D. (2;-5)

Hiển thị đáp án

Đáp án: D

Giải thích:

$y\text{'}=3x^2-6x; y\text{'}=0$

$\iff [\begin{array}{l}x=0\Rightarrow y_{CĐ}=-1\\ x=2\Rightarrow y_{CT}=-5\end{array}$

Câu 9. Số điểm cực trị của hàm số $y=\frac{x^2-x-2}{x+1}$ là

A. 0

B. 1

C. 2

D. 3

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $y=\frac{x^2-x-2}{x+1}=x-2$ hàm số không có cực trị.

Câu 10. Hàm số nào sau đây không có điểm cực trị

A. y = x²

B. y = x³

C. y = x⁴

D. y = -x²

Lời giải

Hiển thị đáp án

Đáp án: B

Giải thích:

Hàm số y = x³ không có cực trị.

Câu 11. Tổng các điểm cực trị của hàm số $y=\frac{1}{3}{x}^3-\frac{5}{2}{x}^2+6x-1$ bằng

A. 4

B. 2

C. 5

D. 6

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $y\text{'}=x^2-5x+6 =0$

$\Rightarrow x_1+x_2=5$

Câu 12. Tích các điểm cực trị của hàm số $y= \frac{1}{3}{x}^3+4x^2-9x-2026$ bằng:

A. -8

B. -9

C. 2

D. 10

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có $y\text{'}=x^2+8x-9 \Rightarrow x_1{x}_2=-9$

Câu 13. Biết hàm số (C): $y=\frac{1}{3}{x}^3-\frac{3}{2}{x}^2+2x+1$ có hai điểm cực trị là x₁,x_2. Đẳng thức nào sau đây đúng?

A. $x_1+x_2=2$

B. $x_1+x_2=3$

C. $x_1+x_2=-3$

D. $x_1+x_2=3$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $y\text{'}=x^2-3x+2=0$

$\iff [\begin{array}{l}{x}_1=1\\ x_2=2\end{array}$

$\Rightarrow x_1+x_2=3.$

Câu 14. Điểm cực tiểu của đồ thị hàm số (C): $\left|x\right|(x+2)$là

A. x = 0

B. x = 1

C. x = -2

D. x = 2

Hiển thị đáp án

Đáp án: A

Giải thích:

Với $x>0\Rightarrow y=x^2+2x$

$\Rightarrow y\text{'}=2x+2>0$

Với $x<0\Rightarrow y=-x^2-2x$

$\Rightarrow y\text{'}=-2x-2>0$

Với x = 0 $\Rightarrow$y = 0.

Hàm số đạt cực tiểu tại x = 0.

Câu 15. Một hàm số y=f(x) liên tục trên R và có đạo hàm $f\text{'}\left(x\right)=(x+1){(x-1)}^2(x^2-4)$ . Hỏi hàm số đã cho có bao nhiêu điểm cực trị?

A. 5

B. 3

C. 8

D. 4

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $f\text{'}\left(x\right)=0\iff [\begin{array}{l}x=\pm 1\\ x=\pm 2\end{array}$

Chỉ có $x=-2;x=-1;x=2$ là nghiệm bội lẻ nên hàm số đạt cực trị tại $x=-2;x=-1;x=2$

Câu 16. Cho hàm số y=f(x) có đạo hàm $f\text{'}\left(x\right)=x^2(x^2-1), \forall x\in R$. Hỏi hàm số y=f(x) đạt cực đại tại điểm nào dưới đây?

A. x=1

B. x= -1

C. x=0

D. x=2

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $f\text{'}\left(x\right)=0\iff [\begin{array}{l}x=0\\ x=\pm 1\end{array}$

Chỉ có $x=\pm 1$ là nghiệm bội lẻ nên hàm số đạt cực trị tại $x=\pm 1$

Câu 17. Cho hàm số y = f(x) có đạo hàm f^'(x) = x²⁰¹⁹(x²⁰²⁰ - 1), $\forall x\in R$ . Hỏi hàm số có bao nhiêu điểm cực trị?

A. 1

B. 2

C. 3

D. Vô số

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $f\text{'}\left(x\right)=0$

$\iff [\begin{array}{l}x=0\\ x=\pm 1\end{array}$ (đều là nghiệm bội lẻ)

Hàm số đạt cực trị tại x=0; x = $\pm 1$

Câu 18. Hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên

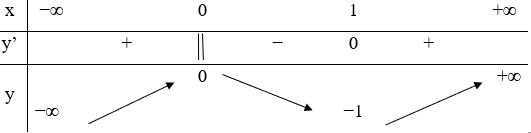
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng một cực trị

B. Hàm số có giá trị cực tiểu bằng 1

C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1

D. Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1.

Hiển thị đáp án

Đáp án: D

Giải thích:

Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1

Câu 19. Hàm số y=f(x) có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng

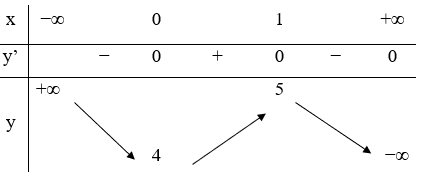
A. y_CĐ = 5

B. y_CT = 0

C. min y = 4

D. max y = 5

Hiển thị đáp án

Đáp án: A

Giải thích:

Giá trị cực đại của hàm số là 5.

Câu 20. Cho hàm số y=f(x) có bảng biến thiên như sau

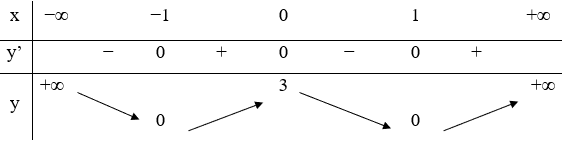
Mệnh đề nào dưới đây sai?

A. Hàm số có ba điểm cực trị

B. Hàm số có giá trị cực đại bằng 3

C. Hàm số có giá trị cực đại bằng 0

D. Hàm số có hai điểm cực tiểu

Hiển thị đáp án

Đáp án: C

Giải thích:

Hàm số có giá trị cực đại bằng 3 nên đáp án C sai.

Câu 21. Hàm số y=f(x) xác định, liên tục trên đoạn [2;4] và có bảng biến thiên như sau

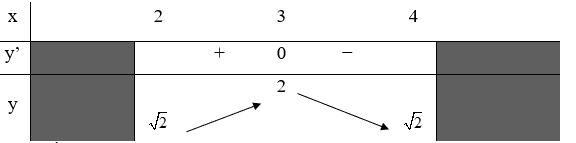
Mệnh đề nào sau đây đúng?

A. Hàm số có ba điểm cực trị

B. Hàm số có một điểm cực trị

C. Cực đại của hàm số bằng 3

D. Cực đại của hàm số bằng $\sqrt{2}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Hàm số có một điểm cực trị.

Câu 22. Hàm số y=f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.

Hỏi hàm số có bao nhiêu điểm cực trị?

A. 1

B. 2

C. 3

D. 0

Hiển thị đáp án

Đáp án: C

Giải thích:

Đạo hàm đổi dấu 3 lần nên hàm số có 3 điểm cực trị.

Câu 23. Hàm số y=f(x) xác định, liên tục trên R\{0} và có bảng xét dấu đạo hàm như hình vẽ.

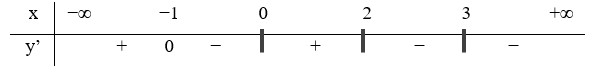
Hỏi hàm số có bao nhiêu điểm cực trị?

A. 1

B. 2

C. 3

D. 4

Hiển thị đáp án

Đáp án: C

Giải thích:

Đạo hàm đổi dấu 3 lần nên hàm số có 3 điểm cực trị.

Câu 24. Hàm số y=f(x) xác định, liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.

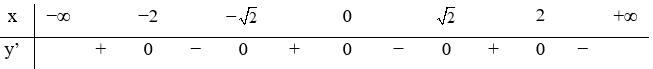
Hàm số y = f(-x) có bao nhiêu điểm cực trị?

A. 6

B. 4

C. 3

D. 5

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:$y=f\left(-x\right)\Rightarrow y^{\text{'}}=-f^{\text{'}}\left(-x\right)$ nên số cực trị của hàm $y=f\left(-x\right)$ cũng chính là số cực trị của hàm số $y=f\left(x\right)$ (vì số lần đổi dấu của đạo hàm là như nhau)

Quan sát bảng xét dấu của hàm $y=f\left(x\right)$ ta thấy đạo hàm đổi dấu 5 lần.

Vậy hàm số $y=f\left(-x\right)$ có 5 điểm cực trị.

Câu 25. Hàm số y = f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ. Hỏi hàm số y = f(2x+1) có bao nhiêu điểm cực trị?

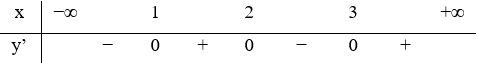
A. 3

B. 2

C. 1

D. 4

Hiển thị đáp án

Đáp án: A

Giải thích:

Chọn $f^{\text{'}}\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)$

$\Rightarrow f^{\text{'}}(2x+1)=2x.(2x-2).(2x-3)$

Ta có:

$y^{\text{'}}=2f^{\text{'}}\left(2x+1\right)$

$=4x.(2x-2).(2x-3);$

$$\begin{gathered} y^{\text{'}}=0\iff x=\left\{0;1;\frac{3}{2}\right\} \\ \left\{1, 2\right\} \end{gathered}$$

Vậy hàm số đã cho có 3 điểm cực trị.

Câu 26. Hàm số y =f(x) liên tục trên $R\left|\right\{0\}$ và có bảng biến thiên như hình vẽ.

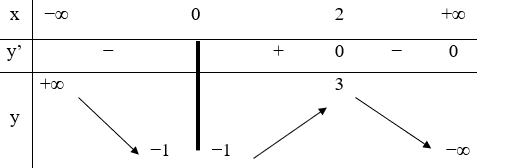
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đạt cực tiểu tại x = 0

B. Hàm số đạt cực đại tại x = 3

C. Giá trị cực đại của hàm số bằng 3

D. Giá trị cực tiểu của hàm số bằng -1

Hiển thị đáp án

Đáp án: C

Giải thích:

Hàm số đạt cực đại tại $x=2$ và giá trị cực đại $y=3.$

Câu 27. Hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số y=f(-x+1) đạt cực đại tại điểm

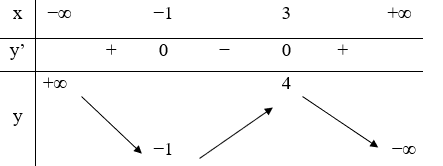
A. x = -2

B. x = 3

C. x = 2

D. x = 0

Hiển thị đáp án

Đáp án: C

Giải thích:

Chọn $f^{\text{'}}\left(x\right)=\left(x+1\right)\left(x-3\right)$

$\Rightarrow f^{\text{'}}\left(-x+1\right)=\left(-x+2\right)\left(-x-2\right)$

$=(x-2)(x+2)$

Ta có $y^{\text{'}}=-f^{\text{'}}\left(-x+1\right)$

$=-\left(-x-2\right)\left(x+2\right);$

$y^{\text{'}}=0\iff x=\left\{-2;2\right\}$

Dựa vào bảng biến thiên, ta được $x=2$ là điểm cực đại của hàm số.

Câu 28. Hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ bên.

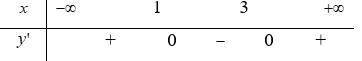
Hàm số g(x) = f(x-1) đạt cực tiểu tại điểm

A. x = 1

B. x = -1

C. x = 3

D. x = -2

Hiển thị đáp án

Đáp án: A

Giải thích:

Chọn $f^{\text{'}}\left(x\right)=x\left(x-2\right)$

$\Rightarrow f^{\text{'}}\left(x-1\right)=\left(x-1\right)\left(x-3\right)$

Ta có: $y^{\text{'}}=f^{\text{'}}\left(x-1\right)=\left(x-1\right)\left(x-3\right);$

$y^{\text{'}}=0\iff x=\left\{1;3\right\}$

Bảng xét dấu $y^{\text{'}}$

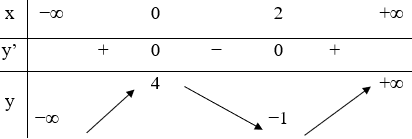
Dựa vào bảng xét dấu, ta được $x=1$ là điểm cực tiểu của hàm số.

Câu 29. Hàm số y=f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.

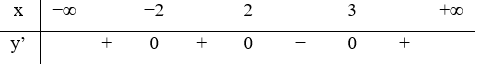
Số điểm cực trị của hàm số y=g(x)=f(1-x²) là

A. 5

B. 0

C. 3

D. 1

Hiển thị đáp án

Đáp án: D

Giải thích:

Chọn $f^{\text{'}}\left(x\right)={\left(x+2\right)}^2\left(x-2\right)\left(x-3\right)$

$\Rightarrow f^{\text{'}}\left(1-x^2\right)$$={(3-x^2)}^2(-1-x^2)(-2-x^2)$

Do đó $y^{\text{'}}=-2x{f}^{\text{'}}\left(1-x^2\right)$

$=-2x{(x^2-3)}^2(x$²+1)(x²+2)

Phương trình $y^{\text{'}}=0$ có duy nhất 1 nghiệm $x=0$ là nghiệm đơn

Vậy hàm số đã cho có duy nhất 1 điểm cực trị.

Câu 30. Hàm số y=f(x) liên tục trên $R\backslash \left\{3\right\}$ và có bảng xét dấu đạo hàm như hình vẽ.

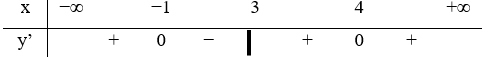
Số điểm cực trị của hàm số y = g(x) = f(x²+2x+3) là

A. 4

B. 1

C. 3

D. 2

Hiển thị đáp án

Đáp án: C

Giải thích:

Hàm số $y=f\left(x\right)$ có hai điểm cực trị là $x=-1;x=3$

Chọn $f^{\text{'}}\left(x\right)=\left(x+1\right)\left(x-3\right)$

$\Rightarrow f^{\text{'}}\left(x^2+2x+3\right)$$=(x^2+2x+4)(x^2+2x)$

Ta có

$y^{\text{'}}=\left(2x+2\right)f^{\text{'}}\left(x^2+2x+3\right)$

$=(2x+2).(x^2+2x+4).(x^2+2x);$

$y^{\text{'}}=0\iff x=\left\{-2;-1;0\right\}$

Bảng xét dấu $y^{\text{'}}$

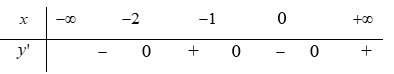
Dựa vào bảng xét dấu, ta được $y=g\left(x\right)$ có 3 điểm cực trị.

Câu 31. Cho hàm số y = x⁴ - 2x² - 2 (2). Khẳng định nào sau đây là đúng?

A. Hàm số (2) đạt cực đại tại y = -2

B. Hàm số (2) đạt giá trị cực đại tại y = -2

C. Đồ thị hàm số (2) có điểm cực đại là y = -2

D. Hàm số (2) có giá trị cực đại là y = -2

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: y' = 4x³ - 4x, y'' = 12x² - 4

y''(-1) = 8 > 0; y''(1) = 8 > 0

Do đó hàm số đạt cực đại tại x = 0 và có giá trị cực đại là y(0)=-2

Câu 32. Hàm số y = cosx đạt cực trị tại những điểm

Hiển thị đáp án

Đáp án: A

Giải thích:

y' = -sinx; y'' = -cosx. y' = 0 <=> -sinx = 0 <=> x = kπ

y''(kπ) = ±1. Do đó hàm số đạt cực trị tại x = kπ

Câu 33. Với giá trị nào của m, hàm số y = x³ - 2x² + mx - 1 không có cực trị?

Hiển thị đáp án

Đáp án: A

Giải thích:

y' = 3x² - 4x + m. Hàm số không có cực trị <=> y’=0 vô nghiệm hoặc có nghiệm kép <=> Δ' ≤ 0 <=> 2² - 3m ≤ 0 <=> m ≥ 4/3

Do đó hàm số không có cực trị khi m ≥ 4/3

Câu 34. Với giá trị nào của m, hàm số y = -mx⁴ + 2(m - 1)x² + 1 - 2m có một cực trị

A.0 ≤ m ≤ 1

B. m > 1 hoặc m < 0

C. 0 < m < 1

D. 0 < m ≤ 1

Hiển thị đáp án

Đáp án: A

Giải thích:

Xét hàm số y = -mx⁴ +2(m - 1)x² + 1 - 2m(1)

TH1: m = 0 (1) trở thành y = -2x² + 1

Vậy với m = 0 hàm số luôn có một cực trị.

TH2: m ≠ 0. y' = -4mx³ + 4(m - 1)x

Để hàm số (1) có một cực trị thì 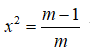vô nghiệm hoặc có nghiệm kép bằng 0

Kết hợp cả hai trường hợp ta có 0 ≤ m ≤ 1

Câu 35. Giá trị của m để hàm số y = x³ - 3mx² + (m² - 1)x + 2 đạt cực đại tại x = 2 là:

A. m = 1

B. m = 11

C. m = -1

D. Không tồn tại.

Hiển thị đáp án

Đáp án: B

Giải thích:

y' = 3x² - 6mx + m² - 1; y'' = 6x - 6m

Hàm số đạt cực đại tại x = 2 khi

Câu 36. Với giá trị nào của m, hàm số y = (x - m)³ - 3x đạt cực tiểu tại điểm có hoành độ x = 0?

A. m = 1

B. m = -1

C. m = 0

D. Không tồn tại

Hiển thị đáp án

Đáp án: B

Giải thích:

Xét y = x³ - 3mx² + (3m² - 3)x - m²

Ta có: y' = 3² - 6mx + 3m² - 3, y'' = 6x - 6m

Hàm số đạt cực tiểu tại điểm có hoành độ x = 0 khi

Câu 37. Với giá trị nào của m, đồ thị hàm số y = x⁴ - 2mx² + m ⁴ + 2m có ba điểm cực trị tạo thành tam giác đều?

A. m = 0

B. m = ∛3

C.-∛3

D. Không tồn tại

Hiển thị đáp án

Đáp án: B

Giải thích:

y' = 4x³ - 4mx = 4x(x² - m)

Hàm số có ba điểm cực trị => y’=0 có ba nghiệm phân biệt <=> m > 0.

Khi đó đồ thị hàm số có ba điểm cực trị là :

A(0; m⁴ + 2m), B(-√m; m⁴ - m² + 2m), C(√m; m⁴ - m² + 2m)

ΔABC đều khi AB=AC

Đối chiếu với điều kiện tồn tại cực trị ta có m = ∛3 là giá trị cần tìm.

Câu 38. Với giá trị nào của m, đồ thị hàm số y = x³ - 3mx² + 3(m² - 1)x - m ³ + m có điểm cực đại B, điểm cực tiểu C thỏa mãn OC = 3OB, với O là gốc tọa độ.

A. m = 1/2

B. m = 2

C. m = 1/2 hoặc m = 2

D. Không tồn tại

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có y' = 3x² - 6mx + 3(m² - 1).

Hàm số có hai cực trị => y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=> (3m)² - 3.3(m² - 1) > 0 <=> 9 > 0 đúng với mọi m. Ta có điểm cực đại là B(m - 1; -2m + 2) và cực tiểu là C(m + 1; -2m - 2)

Câu 39. Điểm cực tiểu của hàm số y = x⁴ + 4x² + 2 là:

A. x = 1

B. x = √2

C. x = 0

D. Không tồn tại

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: y' = 4x³ + 8x, y'' = 12x² + 8. y' = 0 <=> 4x(x² + 2) = 0 <=> x = 0

y''(0) = 2 > 0. Do đó hàm số đạt cực tiểu tại x = 0

Câu 40. Cho hàm số y = x³ - 3x² - 6x + 8 (C). Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (C) là:

A. y = 6x - 6

B. y = -6x - 6

C. y = 6x + 6

D. y = -6x + 6

Hiển thị đáp án

Đáp án: D

Giải thích:

Cách 1: Ta có y’=3x²-6x-6 ; y”=6x - 6

Do đó đồ thị hàm số có điểm cực trị là A(1 + √3; -6√3) và B(1 - √3; 6√3) .

Phương trình đường thẳng đi qua hai điểm cực trị là:

Cách 2: Ta có:

Gọi x₁, x₂ là nghiệm của phương trình y’(x)= 3x²-6x-6=0 . Khi đó ta có A(x₁, y(x₁)), BA(x₂, y(x₂)) là hai cực trị của đồ thị hàm số C với y'(x₁) = y'(x₂) = 0 .

Do đó ta có:

Vậy A, B thuộc đường thẳng y= - 6x+6.

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Giá trị lớn nhất, giá trị nhỏ nhất của hàm số có đáp án

Trắc nghiệm Đường tiệm cận có đáp án

Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số có đáp án

Trắc nghiệm Ôn tập chương 1 - Ứng dụng đạo hàm để khảo sát và vẽ đồ thi của hàm số có đáp án

Trắc nghiệm Lũy thừa có đáp án