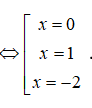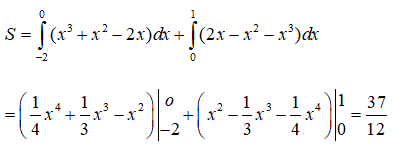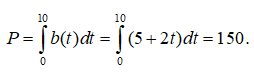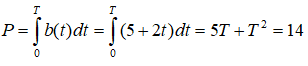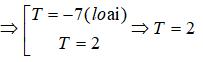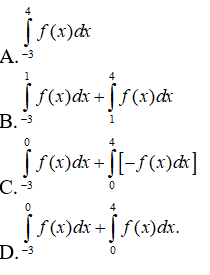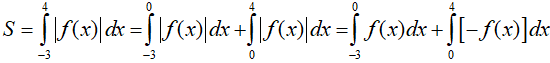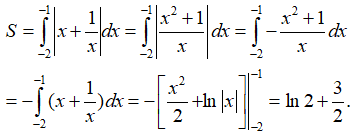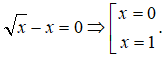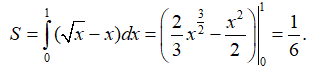TOP 40 câu Trắc nghiệm Ứng dụng tích phân (có đáp án 2024) - Toán 12

Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 3: Ứng dụng tích phân có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 3.

1 2,062 22/12/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 12 Bài 3: Ứng dụng tích phân

Bài giảng Trắc nghiệm Toán 12 Bài 3: Ứng dụng tích phân

Câu 1. Tính diện tích các hình phẳng giới hạn bởi: Đồ thị các hàm số $y = x^{2} - 4, y = - x^{2} - 2 x$ và hai đường thẳng $x = - 3, x = - 2$ ;

A. $\frac{11}{6}$

B. $\frac{11}{3}$

C. $\frac{22}{3}$

D. $\frac{19}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Dựa vào hình vẽ ta thấy diện tích hình phẳng cần tìm là:

$S = \int_{- 3}^{- 2} |(x^{2} - 4) - (- x^{2} - 2 x)| d x$

$= \int_{- 3}^{- 2} [(x^{2} - 4) - (- x^{2} - 2 x)] d x$

$= \int_{- 3}^{- 2} (2 x^{2} + 2 x - 4) d x$

$= (2 \frac{x^{3}}{3} + 2 \frac{x^{2}}{2} - 4 x) |\begin{matrix} - 2 \\ - 3 \end{matrix} = \frac{11}{3}$

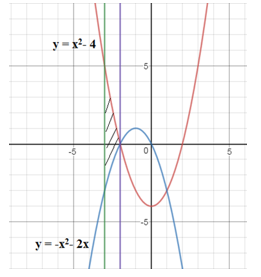
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 2)

Câu 2: Đồ thị hai hàm số $y = x^{2} - 4$ và $y = - x^{2} - 2 x$

A. 8

B. 10

C. 20

D. 9

Hiển thị đáp án

Đáp án: D

Giải thích:

Phương trình hoành độ giao điểm đồ thị hai số đã cho là:

$x^{2} - 4 = - x^{2} - 2 x$

$\Leftrightarrow x^{2} + x - 2 = 0$

$\Leftrightarrow [\begin{matrix} x = 1 \\ x = - 2 \end{matrix}$

Dựa vào hình vẽ ở câu A. ta có:

$S = \int_{- 2}^{1} |(x^{2} - 4) - (- x - 2 x)| d x$

$= \int_{- 2}^{1} [- (2 x^{2} + 2 x - 4)] d x$

$= (- 2 \frac{x^{3}}{3} - 2 \frac{x^{2}}{2} + 4 x) |\begin{matrix} 1 \\ - 2 \end{matrix} = 9$

Câu 3: Đồ thị hàm số $y = x^{3} - 4 x$ , trục hoành, đường thẳng $x = - 2$ và đưởng thẳng $x = 4$ .

A. 44

B. 24

C. 48

D. 28

Hiển thị đáp án

Đáp án: A

Giải thích:

Diện tích cần tìm $S = \int_{- 2}^{1} |x^{3} - 4 x| d x$

Ta có: $x^{3} - 4 x = x (x^{2} - 4) = 0$

$\Leftrightarrow [\begin{matrix} x = 0 \\ x = \pm 2 \end{matrix}$

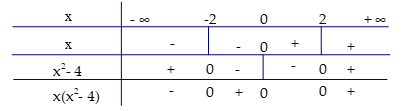
Ta có bảng xét dấu sau:

Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 4)

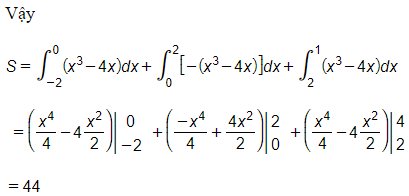
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 1)

Câu 4: Hàm số $y = x^{4} - 4 x^{2} + 4, y = x^{2}$ , trục tung và đường thẳng

A. $\frac{38}{25}$

B. $\frac{38}{35}$

C. $\frac{38}{15}$

D. $\frac{38}{5}$

Hiển thị đáp án

Đáp án: C

Giải thích:

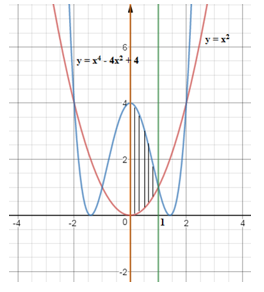
Diện tích hình phẳng cần tìm là:

$S = \int_{0}^{1} |x^{4} - 4 x^{2} + 4 - x^{2}| d x$

$= \int_{0}^{1} |x^{4} - 5 x^{2} + 4| d x$

Vì $x^{4} - 5 x^{2} + 4 = (x^{2} - 1) (x^{2} - 4) \geq 0$

$\forall x \in [0; 1]$

Nên

$S = \int_{0}^{1} (x^{4} - 5 x^{2} + 4) d x$

$= (\frac{x^{5}}{5} - \frac{5 x^{3}}{3} + 4 x) |\begin{matrix} 1 \\ 0 \end{matrix}$

$= \frac{1}{5} - \frac{5}{3} + 4 = \frac{38}{15}$

Câu 5: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y = x^{2} + 1$ và $y = 3 - x$

A. $\frac{6}{2}$

B. $\frac{5}{2}$

C. $\frac{11}{2}$

D. $\frac{9}{2}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Hoành độ giao điểm đồ thị hai hàm số $y = x^{2} + 1$ và $y = 3 - x$ là nghiệm của phương trình $x^{2} + 1 = 3 - x$

$\Leftrightarrow x^{2} + x - 2 = 0$

$\Leftrightarrow [\begin{matrix} x = 1 \\ x = - 2 \end{matrix}$

Vậy diện tích cần tìm là:

$S = \int_{- 2}^{1} |(x^{2} + 1) - (3 - x)| d x$

$= \int_{- 2}^{1} |x^{2} + x - 2| d x$

$= - \int_{- 2}^{1} (x^{2} + x - 2) d x$

$= - (\frac{x^{3}}{3} + \frac{x^{2}}{2} - 2 x) |\begin{matrix} 1 \\ - 2 \end{matrix}$

$= \frac{9}{2}$

Câu 6: Tính diện tích hình phẳng giới hạn bởi các đường có phương trình $x = y^{3}, y = 1$ và $x = 8$

A. $\frac{17}{4}$

B. $\frac{17}{2}$

C. $\frac{17}{8}$

D. $\frac{27}{4}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Tung độ giao điểm của đường cong $x = y^{3}$ và đường thẳng $x = 8$ là nghiệm của phương trình $y^{3} = 8 \Leftrightarrow y = 2$ . Vậy diện tích cần tìm là:

$S = \int_{1}^{2} |y^{3} - 8| d y$

$= \int_{1}^{2} (y^{3} - 8) d y$

$= - (\frac{y^{4}}{4} - 8 y) |\begin{matrix} 2 \\ 1 \end{matrix}$

$= - [(\frac{16}{4} - 16) - (\frac{1}{4} - 8)]$

$= \frac{17}{4}$

Câu 7: Đồ thị hai hàm số $y = \sqrt{x}, y = 6 - x$ và trục hoành.

A. $\frac{23}{3}$

B. $\frac{22}{3}$

C. $\frac{25}{3}$

D. $\frac{29}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $y = \sqrt{x} \Leftrightarrow x = y^{2} (y \geq 0);$

$y = 6 - x \Leftrightarrow x = 6 - y$

Tung độ giao điểm của hai đường thẳng $x = y^{2}, x = 6 - y$ là nghiệm của phương trình $y^{2} = 6 - y$ $\Leftrightarrow y^{2} + y - 6 = 0$ $\Leftrightarrow [\begin{matrix} y = - 3 (L vi y \geq 0) \\ y = 2 \end{matrix}$

Vậy diện tích cần tìm là $S = \int_{0}^{2} |y^{2} - (6 - y)| d y$

$= \int_{0}^{2} |y^{2} + y - 6| d y$

$= - \int_{0}^{2} (y^{2} + y - 6) d y$

$= - (\frac{y^{3}}{3} + \frac{y^{2}}{2} - 6 y) |\begin{matrix} 2 \\ 0 \end{matrix}$

$= - (\frac{8}{3} + \frac{4}{2} - 12) = \frac{22}{3}$

Câu 8. Tính diện tích các hình phẳng giới hạn bởi: Đồ thị các hàm số $y = 4 - x^{2},$ $y = - x + 2$

A. $\frac{9}{2}$

B. $\frac{22}{5}$

C. $\frac{11}{3}$

D. $\frac{25}{3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $4 - x^{2} = - x + 2$

$\Leftrightarrow x^{2} - x - 2 = 0$

$\Leftrightarrow [\begin{matrix} x = - 1 \\ x = 2 \end{matrix}$

Vậy diện tích hình phẳng cần tìm là:

$S = \int_{- 1}^{2} |(- x + 2) - (4 - x^{2})| d x$

$= \int_{- 1}^{2} |x^{2} - x - 2| d x$

$= - \int_{- 1}^{2} (x^{2} - x - 2) d x$

$= - (\frac{x^{3}}{3} - \frac{x^{2}}{2} - 2 x) |\begin{matrix} 2 \\ - 1 \end{matrix}$

$= - [(\frac{8}{3} - \frac{4}{2} - 4) - (- \frac{1}{3} - \frac{1}{2} + 2)]$

$= \frac{9}{2}$

Câu 9. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số $y = \sqrt{e^{x}}$ và các đường thẳng $y = 0$ , $x = 0$ và $x = 2$ . Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng (H) quanh trục Ox được tính bởi công thức nào sau đây?

A. $V = π \int_{0}^{2} e^{x} d x$ .

B. $V = π \int_{0}^{2} e^{2 x} d x$ .

C. $V = π \int_{0}^{2} e^{x^{2}} d x$ .

D. $V = \int_{0}^{2} e^{x^{2}} d x$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $V = π \int_{0}^{2} {(\sqrt{e^{x}})}^{2} d x$

$= π \int_{0}^{2} e^{x} d x$ .

Câu 10. Gọi (H) là hình phẳng giới hạn bởi đồ thị $y = e^{x}$ , trục Ox và hai đường thẳng $x = 0$ , $x = 1$ . Thể tích của khối tròn xoay khi quay (H) xung quanh trục Ox là

A. $\frac{π}{2} (e^{2} - 1)$ .

B. $π (e^{2} + 1)$ .

C. $\frac{π}{2} (e^{2} + 1)$ .

D. $π (e^{2} - 1)$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

$V = π \int_{0}^{1} {(e^{x})}^{2} dx$

$= π \int_{0}^{1} e^{2 x} dx$

$= {\frac{π}{2} e^{2 x}|}_{0}^{1}$

$= \frac{π}{2} (e^{2} - e^{0})$

$= \frac{π}{2} (e^{2} - 1)$

Câu 11. Hãy tính diện tích phần tô đậm trong hình vẽ dưới đây.

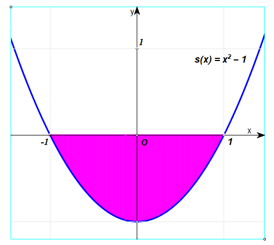
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 6)

A. $\frac{4}{3}$ .

B. $\frac{3}{4}$ .

C. 1.

D. $\frac{π}{2}$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Cách 1: Ta có $x^{2} - 1 \leq 0, \forall x \in [- 1; 1]$

Do đó diện tích phần tô đậm là

$S = \int_{- 1}^{1} |x^{2} - 1| dx$

$= \int_{- 1}^{1} (1 - x^{2}) dx$

$= {(x - \frac{x^{3}}{3})|}_{- 1}^{1}$

$= \frac{4}{3}$

Cách 2: Công thức nhanh tính diện tích $S = \frac{2}{3} B h$

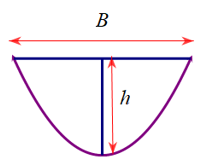
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 7)

Áp dụng công thức với $B = 2$ , $h = 1$ ta có:

$S = \frac{2}{3} B h$

$= \frac{2}{3} .2.1 = \frac{4}{3}$

Câu 12. Phần hình phẳng (H) được gạch chéo trong hình vẽ dưới đây được giới hạn bởi đồ thị hàm số $y = f (x)$ , $y = x^{2} + 4 x$ và hai đường thẳng $x = - 2; x = 0$ .

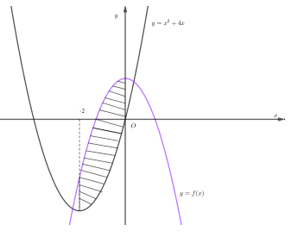
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 8)

Biết $\int_{- 2}^{0} f (x) d x = \frac{4}{3}$ . Diện tích hình (H) là

A. $\frac{7}{3}$ .

B. $\frac{16}{3}$ .

C. $\frac{4}{3}$ .

D. $\frac{20}{3}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Diện tích hình (H) là :

$S = \int_{- 2}^{0} [f (x) - (x^{2} + 4 x)] d x$

$= \int_{- 2}^{0} f (x) d x - \int_{- 2}^{0} (x^{2} + 4 x) d x$

$= \frac{4}{3} - (\frac{x^{3}}{3} + 2 x^{2}) |\begin{array}{l} 0 \\ - 2 \end{array}$

$= \frac{4}{3} + \frac{{(- 2)}^{3}}{3} + 2 {(- 2)}^{2} = \frac{20}{3}$

Vậy diện tích hình (H) là $S = \frac{20}{3}$ .

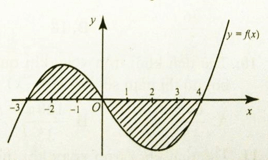
Câu 13. Cho hàm số $y = f (x)$ liên tục trên $[0; 8]$ và có đồ thị như hình vẽ.

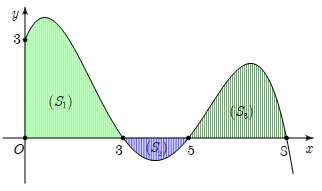
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 9)

Trong các giá trị sau, giá trị nào lớn nhất?

A. $\int_{0}^{3} f (x) d x$ .

B. $\int_{0}^{1} f (x) d x$ .

C. $\int_{0}^{8} f (x) d x$ .

D. $\int_{0}^{5} f (x) d x$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có:

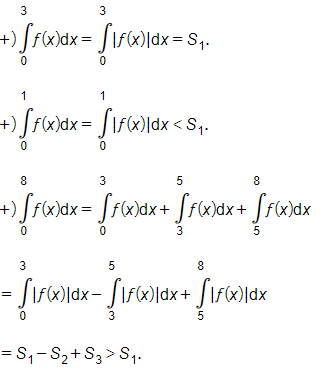
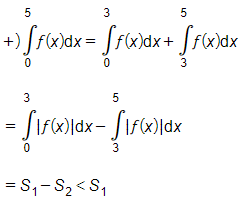
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 1)

Vậy $\int_{0}^{8} f (x) d x$ là giá trị lớn nhất.

Câu 14. Một ô tô đang chuyển động đều với vận tốc $15 m / s$ thì phía trước xuất hiện một vật nên người lái xe đạp phanh gấp. Kể từ điểm đó, ô tô chuyển động chậm dần đều với gia tốc $- a (m / s^{2})$ , $a > 0$ . Biết ô tô chuyển động được $20 m$ nữa thì dừng hẳn. Hỏi thuộc khoảng nào dưới đây ?

A. (6;7)

B. (4;5)

C. (5;6)

D. (3;4)

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $v (t) = 15 - a t$ .

Tại thời điểm ô tô dừng hẳn ta có $v (t) = 0 \Leftrightarrow 15 - a t = 0$

$\Leftrightarrow t = \frac{15}{a}$

Do ô tô đi được thêm 20m nên ta có:

$\int_{0}^{\frac{15}{a}} v (t) d t = \int_{0}^{\frac{15}{a}} (15 - a t) d t = 20$

$\Leftrightarrow {(15 t - \frac{1}{2} a t^{2})|}_{0}^{\frac{15}{a}} = 20$

$\Leftrightarrow 15. \frac{15}{a} - \frac{1}{2} a . \frac{15^{2}}{a^{2}} = 20$

$\Leftrightarrow \frac{225}{a} - \frac{225}{2 a} = 20$

$\Leftrightarrow a = 5, 625$

Suy ra $a \in (5; 6)$ .

Câu 15. Một chiếc ô tô đang chạy với vận tốc $15 m / s$ thì người lái xe hãm phanh. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với vận tốc $v (t) = - 3 t + 15 (m / s)$ , trong đó t ( giây). Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét?

A. 38m.

B. 37,2m.

C. 37,5m.

D. 37m.

Hiển thị đáp án

Đáp án: C

Giải thích:

Thời gian từ lúc ô tô hãm phanh đến lúc dừng hẳn là $- 3 t + 15 = 0 \Leftrightarrow t = 5.$

Quãng đường ô tô di chuyển được từ lúc hãm phanh đến khi dừng hẳn là

$S = \int_{0}^{5} v (t) d t$

$= \int_{0}^{5} (- 3 t + 15) d t$

$= 37, 5 (m)$

Câu 16. Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số $y = x^{2} - 4 x + 3$ và trục hoành quay quanh trục Ox là

A. $\frac{4 π}{3}$ .

B. $\frac{16}{15}$ .

C. $\frac{16 π}{15}$ .

D. $\frac{4}{3}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Hoành độ giao điểm của đồ thị hàm số $y = x^{2} - 4 x + 3$ và trục hoành là nghiệm phương trình $x^{2} - 4 x + 3 = 0$

$\Leftrightarrow [\begin{array}{l} x = 1 \\ x = 3 \end{array}$ .

Do đó, thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số $y = x^{2} - 4 x + 3$ và trục hoành quay quanh trục Ox là

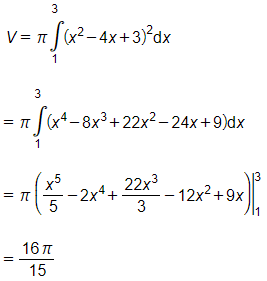
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 1)

Câu 17. Cho hàm số bậc hai $y = a x^{2} + b x + c$ có đồ thị là parabol (P) như hình bên. Gọi D là miền D giới hạn bởi parabol và trục hoành. Tính thể tích khối tròn xoay tạo bởi khi quay hình phẳng quanh trục Ox.

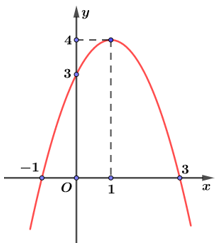
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 10)

A. $V = \frac{64 π}{3}$ .

B. $V = \frac{256 π}{15}$ .

C. $V = \frac{32 π}{3}$ .

D. $V = \frac{512 π}{15}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Dựa vào hình vẽ ta có: $A (- 1; 0), B (3; 0), C (1; 4)$ thuộc (P) nên ta có hệ phương trình:

$\{\begin{cases} a - b + c = 0 \\ 9 a + 3 b + c = 0 \\ a + b + c = 4 \end{cases}$

$\Leftrightarrow \{\begin{cases} a = - 1 \\ b = 2 \\ c = 3 \end{cases}$

$\Rightarrow y = - x^{2} + 2 x + 3$

Thể tích khối tròn xoay:

$V = π \int_{- 1}^{3} {(- x^{2} + 2 x + 3)}^{2} d x$

$= \frac{512 π}{15}$ .

Câu 18. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = \sqrt{x}$ ; tiếp tuyến với đồ thị tại $M (4; 2)$ và trục hoành là

A. $\frac{3}{8}$

B. $\frac{2}{3}$ .

C. $\frac{8}{3}$ .

D. $\frac{1}{3}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Xét hàm số $y = \sqrt{x}$ ta có $y' = \frac{1}{2 \sqrt{x}} \Rightarrow y' (4) = \frac{1}{4}$ .

Phương trình tiếp tuyến của đồ thị tại điểm $M (4; 2)$ là $y = \frac{1}{4} (x - 4) + 2$

$\Leftrightarrow y = \frac{1}{4} x + 1$ .

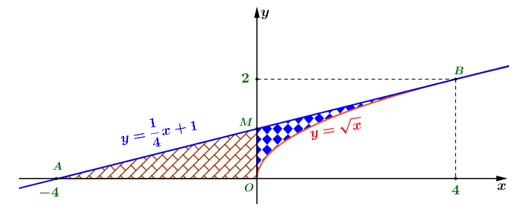
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 11)

Diện tích hình phẳng cần tìm là

$S = S_{O A M} + S_{O M B}$

$= \frac{1}{2} .4.1 + \int_{0}^{4} (\frac{1}{4} x + 1 - \sqrt{x}) d x$

$= \frac{8}{3}$

Câu 19. Một khuôn viên có dạng là một nửa hình tròn đường kính là $4 \sqrt{5} m$ . Trên đó người ta thiết kế một phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh là tâm đường tròn, hai đầu mút của parabol nằm trên đường tròn và cách nhau 4m. Phần còn lại của khuôn viên (không tô đậm) để trồng cỏ.Biết các kích thước cho như hình vẽ và chi phí trồng cỏ là 100.000 đồng $/ m^{2}$ . Số tiền để trồng cỏ là

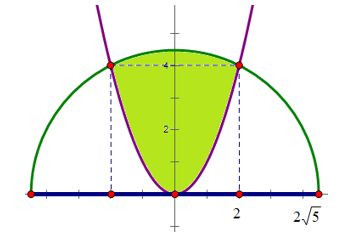
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 12)

A. $3.895.000$ .

B. $1.194.000$ .

C. $1.948.000$ .

D. $2.388.000$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Đồ thị nửa trên đường tròn $y = \sqrt{20 - x^{2}}$ .

Parabol qua gốc tọa độ, nhận trục tung làm trục đối xứng nên phương trình của parabol có dạng $y = a x^{2}$

Vì (P) đi qua $(2; 4)$ nên $(P) : y = x^{2}$ .

Diện tích phần tô đậm: $\int_{- 2}^{2} (\sqrt{20 - x^{2}} - x^{2}) d x$

Diện tích phần trồng cỏ:

$\frac{π {(2 \sqrt{5})}^{2}}{2} - \int_{- 2}^{2} (\sqrt{20 - x^{2}} - x^{2}) d x \approx 19, 48$

Từ đó suy ra chi phí trồng cỏ là:

$19, 48 \times 100.000 = 1.948.000$ đồng.

Câu 20. Người ta xây sân khấu với mặt sàn có dạng hợp của hai đường tròn giao nhau. Bán kính của hai hình tròn lần lượt là 20m và 15m. Khoảng cách giữa hai tâm của hai hình tròn là 30m. Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là nghìn đồng và chi phí làm mỗi mét vuông còn lại là 100 nghìn đồng. Hỏi số tiền làm mặt sàn sân khấu gần với số nào trong các số dưới đây?

A. 202 triệu đồng.

B. 208 triệu đồng.

C. 218 triệu đồng.

D. 200 triệu đồng.

Hiển thị đáp án

Đáp án: A

Giải thích:

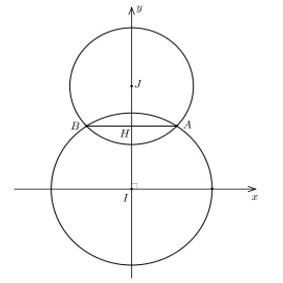
Gọi I,J lần lượt là tâm của hai đường tròn bán kính 20m, 15m.

Gọi A,B là giao của hai đường tròn.

Chọn hệ trục tọa độ Oxy sao cho Oy trùng IJ và Ox song song với AB và I là gốc tọa độ (như hình vẽ).

Khi đó đường tròn tâm I bán kính $R = 20 m$ có phương trình $x^{2} + y^{2} = 400$ .

Vì khoảng cách giữa hai tâm của hai hình tròn là 30m nên $J (0; 30)$ . Do đó đường tròn tâm $J (0; 30)$ bán kính $R = 15 m$ có phương trình $x^{2} + {(y - 30)}^{2} = 225$

Khi đó phần chung của hai đường tròn giới hạn bởi

Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 1)

Diện tích riêng của hai đường tròn là

Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 1)

Vậy số tiền làm mặt sàn sân là gần 202 triệu đồng.

Câu 21. Cho (H) là hình phẳng giới hạn bởi các đồ thị hàm số $y = x^{3} + 2 x^{2}$ và $y = x + 2$ . Thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox bằng bao nhiêu?

A. $V = \frac{162}{35}$ .

B. $V = \frac{648 π}{105}$ .

C. $V = \frac{442}{105}$ .

D. $V = \frac{776 π}{105}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

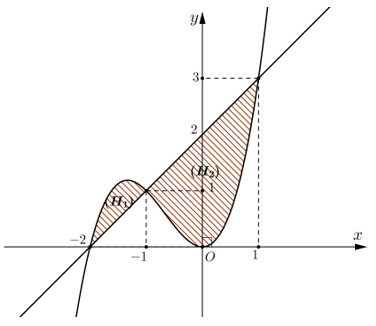
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số $y = x^{3} + 2 x^{2}$ và $y = x + 2$ :

$x^{3} + 2 x^{2} = x + 2$

$\Leftrightarrow x^{3} + 2 x^{2} - x - 2 = 0$

$\Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 1 \\ x = - 2 \end{array}$

Hình phẳng (H) giới hạn bởi hai đồ thị hàm số $y = x^{3} + 2 x^{2}$ và $y = x + 2$ là phần gạch chéo và được chia thành hai hình $(H_{1})$ và $(H_{2})$ (như hình vẽ).

Thể tích $V_{1}$ của khối tròn xoay tạo thành khi quay $(H_{1})$ quanh trục Ox là:

$V_{1} = π \int_{- 2}^{- 1} [{(x^{3} + 2 x^{2})}^{2} - {(x + 2)}^{2}] d x$

Thể tích $V_{2}$ của khối tròn xoay tạo thành khi quay $(H_{2})$ quanh trục Ox là:

$V_{2} = π \int_{- 1}^{1} [{(x + 2)}^{2} - {(x^{3} + 2 x^{2})}^{2}] d x$

Thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox là:

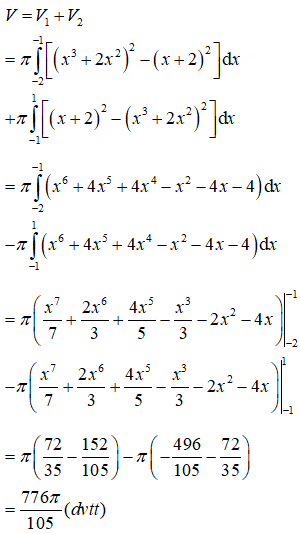
Trắc nghiệm Ứng dụng tích phân có đáp án - Toán lớp 12 (ảnh 1)

Câu 31. Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox.

A. $V = π \int_{a}^{b} f (x) dx$

B. $V = \int_{a}^{b} f^{2} (x) dx$

C. $V = π \int_{a}^{b} |f (x)| dx$

D. $V = π \int_{a}^{b} f^{2} (x) dx$

Hiển thị đáp án

Đáp án: A

Giải thích:

Công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox là

$V = π \int_{a}^{b} f^{2} (x) dx$

Câu 32. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x^{3} - x$ và đồ thị hàm số $y = x - x^{2}$

A. $\frac{9}{4}$

B. $\frac{37}{12}$

C. $\frac{81}{12}$

D. 13

Hiển thị đáp án

Đáp án: B

Giải thích:

$x^{3} - x = x - x^{2}$ $\Leftrightarrow x^{3} + x^{2} - 2 x = 0$ Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy diện tích của hình phẳng tính là

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án B.

Câu 33. Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người).

a) Có bao nhiêu trẻ được sinh trong khoảng thời gian này ( tức là trong 10 năm đầu tiên sau chiến tranh)?

A. 100 triệu B. 120 triệu C. 150 triệu D. 250 triệu.

b) Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.

A. 1 năm B. 2 năm C. 3 năm D. 4 năm.

Hiển thị đáp án

Đáp án: C,B

Giải thích:

a) Để tìm số trẻ mới sinh, chúng ta sẽ tính tích phân tỉ lệ sinh b(t) trên khoảng thời gian 10 năm đầu tiên sau chiến tranh

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy số trẻ được sinh cần tìm là 150 triệu.

Chọn đáp án C.

b) Số lượng trẻ mới sinh trong khoảng thời T bằng:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án B.

Câu 34. Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.

A. 1 năm

B. 2 năm

C. 3 năm

D. 4 năm

Hiển thị đáp án

Đáp án: B

Giải thích:

Số lượng trẻ mới sinh trong khoảng thời T bằng:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 35. Cho đồ thị hàm số y = f(x). Diện tích hình phẳng ( phần gạch sọc ) là:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 36. Diện tích hình phẳng giới hạn bởi $y = x^{2} - x + 3$ và $y = 2 x + 1$ là:

A. $\frac{3}{2}$

B. $- \frac{3}{2}$

C. $\frac{1}{6}$

D. $- \frac{1}{6}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Câu 37. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x + \frac{1}{x}$ , trục hoành, đường thẳng x = -1 và đường thẳng x = -2 là:

A. $\ln 2 + \frac{3}{2}$

B. $\ln 2 + \frac{11}{3}$

C. $\ln 2 + \frac{19}{3}$

D. $\ln 2 + \frac{5}{2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Diện tích giới hạn được tính bởi

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 38. Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y = \sqrt{x}$ và y = 6 - x và trục tung là

A. $\frac{22}{3}$

B. $\frac{11}{3}$

C. $\frac{19}{3}$

D. $\frac{25}{3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 39. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = \sqrt{x} - x$ và trục hoành.

A. 1

B. $\frac{1}{6}$

C. $\frac{5}{6}$

D. $\frac{1}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Xét phương trình

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Khi đó diện tích hình phẳng được tính bởi

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 40. Thể tích khối tròn xoay khi quay quanh trục tung một hình phẳng giới hạn bởi hình tròn tâm I(2;0) bán kính R = 1 là:

A. π²

B. 2π²

C. 4π²

D. 8π²

Hiển thị đáp án

Đáp án: C

Giải thích:

Phương trình đường tròn tâm I(2 ; 0), bán kính R = 1 là :

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Đường tròn cắt trục tung tại hai điểm (0; 1) và( 0; -1).

Vậy ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng có đáp án

Trắc nghiệm Số phức có đáp án

Trắc nghiệm Cộng, trừ và nhân số phức có đáp án

Trắc nghiệm Phép chia số phức có đáp án

Trắc nghiệm Phương trình bậc hai với hệ số thực có đáp án

1 2,062 22/12/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3