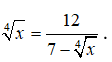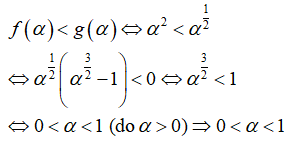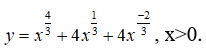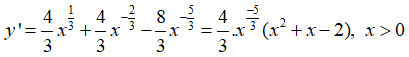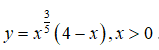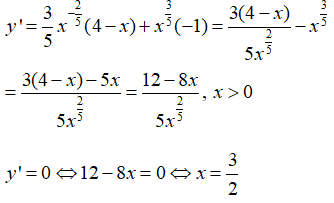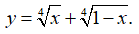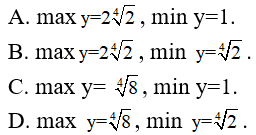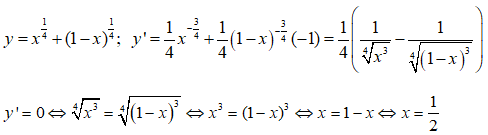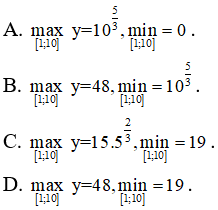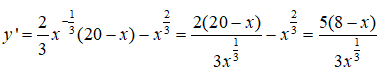TOP 40 câu Trắc nghiệm Hàm lũy thừa (có đáp án 2024) - Toán 12

Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 2: Hàm lũy thừa có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 2.

1 4,377 22/12/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 12 Bài 2: Hàm lũy thừa

Bài giảng Toán 12 Bài 2: Hàm lũy thừa

Câu 1. Tìm tập xác định D của hàm số $y = {(x^{3} - 27)}^{\frac{π}{2}}$ .

A. $D = ℝ \ \{2\}$ .

B. $D = ℝ$ .

C. $D = [3; + \infty)$ .

D. $D = (3; + \infty)$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Áp dụng lý thuyết "Lũy thừa với số mũ không nguyên thì cơ số phải dương".

Do đó hàm số $y = {(x^{3} - 27)}^{\frac{π}{2}}$ xác định khi $x^{3} - 27 > 0 \Leftrightarrow x > 3$ .

Câu 2. Hàm số nào dưới đây có tập xác định không phải là R?

A. $y = {(x^{2} + 1)}^{\frac{1}{2}}$

B. $y = \sqrt{x^{2}}$

C. $y = \frac{x}{x - 1}$

D. $y = \sqrt[3]{x}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Hàm số $y = {(x^{2} + 1)}^{\frac{1}{2}}$ có điều kiện xác định $x^{2} + 1 > 0$ (luôn đúng) nên TXĐ: D = R

Hàm số $y = \sqrt{x^{2}}$ có điều kiện xác định $x^{2} \geq 0$ (luôn đúng) nên TXĐ: D = R

Hàm số $y = \frac{x}{x - 1}$ có điều kiện xác định $x - 1 \neq 0 \Leftrightarrow x \neq 1$ nên TXĐ:

Hàm số $y = \sqrt[3]{x}$ xác định với mọi x nên TXĐ: D = R

Câu 3. (ĐỀ CHÍNH THỨC 2016 – 2017) Tìm tập xác định D của hàm số $y = {(x^{2} - x - 2)}^{- 3}$ .

A. $D = ℝ .$

B. $D = ℝ \ \{- 1; 2\} .$

C. $D = (- \infty; - 1) \cup (2; + \infty) .$

D. $D = (0; + \infty)$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Áp dụng lý thuyết "Lũy thừa với số mũ nguyên âm thì cơ số phải khác 0".

Do đó hàm số đã cho xác định khi $x^{2} - x - 2 \neq 0 \Leftrightarrow \{\begin{cases} x \neq - 1 \\ x \neq 2 \end{cases}$

Câu 4. Chọn khẳng định đúng:

A. Với $n \in N *$ thì $\sqrt[n]{x} = x^{\frac{1}{n}}$ nếu x > 0

B. Với $n \in N *$ thì $\sqrt[n]{x} = x^{\frac{1}{n}}$ nếu $x \geq 0$

C. Với $n \in N *$ thì $\sqrt[n]{x} = x^{\frac{1}{n}}$ nếu x < 0

D. Với $n \in N *$ thì $\sqrt[n]{x} = x^{\frac{1}{n}}$ nếu $x \neq 0$

Hiển thị đáp án

Đáp án: A

Giải thích:

Vì hàm số $y = x^{\frac{1}{n}}$ có số mũ không nguyên nên cơ số phải dương, hay x > 0

Câu 5. Công thức tính đạo hàm của hàm số $y = x^{α}$ là:

A. $y' = α x^{α - 1}$

B. $y' = (α - 1) x^{α - 1}$

C. $y' = α x^{α}$

D. $y' = α x^{α} - 1$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $(x^{α})' = α . x^{α - 1}$

Câu 6. Đẳng thức $(\sqrt[n]{x})' = (x^{\frac{1}{n}})'$ $= \frac{1}{n} x^{- \frac{n - 1}{n}} = \frac{1}{n \sqrt[n]{x^{n - 1}}}$ xảy ra khi:

A. $x < 0$

B. $x > 0$

C. $x \geq 0$

D. $x \in R$

Hiển thị đáp án

Đáp án: B

Giải thích:

Vì $\sqrt[n]{x} = x^{\frac{1}{n}}$ nếu x > 0 nên $(\sqrt[n]{x})' = (x^{\frac{1}{n}})'$ $= \frac{1}{n} x^{- \frac{n - 1}{n}} = \frac{1}{n \sqrt[n]{x^{n - 1}}}$ chỉ đúng nếu x > 0.

Câu 7. Tìm tập xác định D của hàm số $y = {(x^{4} - 3 x^{2} - 4)}^{\sqrt{2}}$ .

A. $D = (- \infty; - 1) \cup (4; + \infty) .$

B. $D = (- \infty; - 2) \cup (2; + \infty) .$

C. $D = (- \infty; - 2] \cup [2; + \infty) .$

D. $D = (- \infty; + \infty) .$

Hiển thị đáp án

Đáp án: B

Giải thích:

Áp dụng lý thuyết "Lũy thừa với số mũ không nguyên thì cơ số phải dương".

Do đó hàm số đã cho xác định khi $x^{4} - 3 x^{2} - 4 > 0$

$\Leftrightarrow (x^{2} - 4) (x^{2} + 1) > 0$

$\Leftrightarrow x^{2} - 4 > 0 \Leftrightarrow [\begin{array}{l} x > 2 \\ x < - 2 \end{array}$

Câu 8. Tìm tập xác định D của hàm số $y = {[x^{2} (x + 1)]}^{\sqrt{π}} .$

A. $D = (0; + \infty) .$

B. $D = (- 1; + \infty) \ \{0\} .$

C. $D = (- \infty; + \infty) .$

D. $D = (- 1; + \infty) .$

Hiển thị đáp án

Đáp án: B

Giải thích:

Hàm số xác định khi $x^{2} (x + 1) > 0 \Leftrightarrow \{\begin{cases} x > - 1 \\ x \neq 0 \end{cases}$

Câu 9. Xét hàm số $y = x^{α}$ trên $(0; + \infty)$ có đồ thị dưới đây, chọn kết luận đúng:

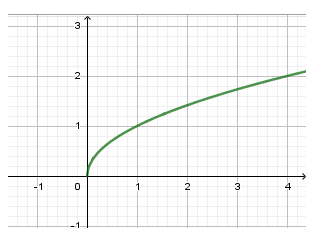
Trắc nghiệm Hàm lũy thừa có đáp án - Toán lớp 12 (ảnh 3)

A. $α = 0$

B. $α = 1$

C. $α > 1$

D. $0 < α < 1$

Hiển thị đáp án

Đáp án: D

Giải thích:

Sử dụng các dáng đồ thị hàm số $y = x^{α}$ ứng với các điều kiện khác nhau của $α$

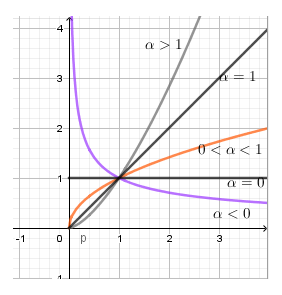
Trắc nghiệm Hàm lũy thừa có đáp án - Toán lớp 12 (ảnh 4)

Từ hình vẽ ta thấy $1 < 2^{α} < 2 \Rightarrow 0 < α < 1$

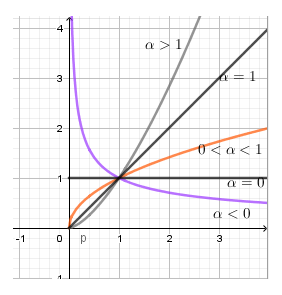
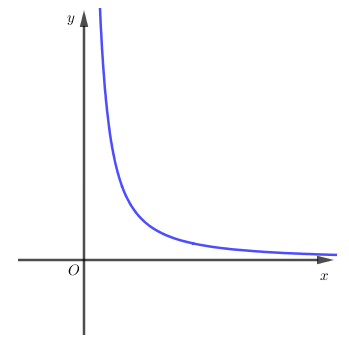
Câu 10. Cho hàm số $y = x^{α}$ có đồ thị như hình dưới. Điều kiện của $α$ là:

Trắc nghiệm Hàm lũy thừa có đáp án - Toán lớp 12 (ảnh 5)

A. $α > 0$

B. $α = 0$

C. $α < 0$

D. $α < 1$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có dáng đồ thị hàm số lũy thừa $y = x^{α}$

Quan sát hình vẽ các dáng đồ thị của hàm số lũy thừa ta thấy điều kiện của $α$ ứng với các đồ thị bài cho là: $α < 0$

Trắc nghiệm Hàm lũy thừa có đáp án - Toán lớp 12 (ảnh 6)

Câu 11. Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% một quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý số tiền lãi sẽ được nhập vào gốc để tính lãi cho quý tiếp theo. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được 1 năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây?

A. 210 triệu.

B. 220 triệu.

C. 212 triệu.

D. 216 triệu.

Hiển thị đáp án

Đáp án: C

Giải thích:

Số tiền nhận về sau 1 năm của 100 triệu gửi trước là $100 {(1 + 2 %)}^{4}$ triệu.

Số tiền nhận về sau 6 tháng của 100 triệu gửi sau là $100 {(1 + 2 %)}^{2}$ triệu.

Vậy tổng số tiền là $100 {(1 + 2 %)}^{4} + 100 {(1 + 2 %)}^{2}$

$= 212, 283216 (\approx 212, 283)$ triệu.

Câu 12. Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?

A. $y = x^{- 4}$

B. $y = x^{4}$

C. $y = x^{- \frac{3}{4}}$

D. $y = \sqrt[3]{x}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Hàm số $y = x^{- 4}$ có tập xác định là $R \ \{0\}$ và có $y' = - 4 x^{- 5}$ nên không đồng biến trên các khoảng xác định (đồng biến trên $(- \infty; 0)$ và nghịch biến trên $(0; + \infty)$ ) loại A

Hàm số $y = x^{- \frac{3}{4}}$ có tập xác định là $(0; + \infty)$ và có $y' = - \frac{3}{4} x^{- \frac{7}{4}} < 0, \forall x \in (0; + \infty)$ nên không đồng biến trên từng khoảng xác định, loại B

Hàm số $y = x^{4}$ có tập xác định là R và có $y' = 4 x^{3}$ nên không đồng biến trên các khoảng xác định, loại C

Hàm số $y = \sqrt[3]{x}$ có tập xác định là R và có $y' = \frac{1}{3 \sqrt[3]{x^{2}}} > 0$ nên hàm số đồng biến trên các khoảng xác định.

Câu 13. Tìm đạo hàm của hàm số $y = {(x^{2} + 1)}^{\frac{e}{2}}$ trên R.

A. $y' = 2 x {(x^{2} + 1)}^{\frac{e}{2} - 1}$

B. $y' = e x \sqrt{{(x^{2} + 1)}^{e - 2}}$

C. $y' = \frac{e}{2} {(x^{2} + 1)}^{\frac{e}{2} - 1}$

D. $y' = {(x^{2} + 1)}^{\frac{e}{2}} \ln (x^{2} + 1)$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $y' = {({(x^{2} + 1)}^{\frac{e}{2}})}^{'}$

$= \frac{e}{2} .2 x {(x^{2} + 1)}^{\frac{e}{2} - 1}$

$= e x {(x^{2} + 1)}^{\frac{e}{2} - 1}$

$= e x \sqrt{{(x^{2} + 1)}^{e - 2}}$

Câu 14. Một người gửi vào ngân hàng số tiền A đồng, lãi suất r mỗi tháng theo hình thức lãi kép. Gửi theo phương thức có kì hạn m tháng. Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau N kì hạn là:

A. $T = A {(1 + m r)}^{N}$

B. $T = A {(1 + r)}^{N}$

C. $T = A {(1 + r)}^{\frac{N}{m}}$

D. $T = N {(1 + m r)}^{A}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau N kì hạn là $T = A {(1 + m r)}^{N}$

Câu 15. Bác An đem gửi tổng số tiền 320 triệu đồng ở hai loại kỳ hạn khác nhau. Bác gửi 140 triệu đồng theo kỳ hạn ba tháng với lãi suất $2, 1 %$ một quý. Số tiền còn lại bác An gửi theo kỳ hạn một tháng với lãi suất $0, 73 %$ một tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi kỳ hạn số tiền lãi sẽ được nhập vào gốc để tính lãi cho kỳ hạn tiếp theo. Sau 15 tháng kể từ ngày gửi bác An đi rút tiền. Tính gần đúng đến hàng đơn vị tổng số tiền lãi thu được của bác An.

A. 36080251 đồng.

B. 36080254 đồng.

C. 36080255 đồng.

D. 36080253 đồng.

Hiển thị đáp án

Đáp án: D

Giải thích:

Số tiền nhận về sau 15 tháng của 140 triệu gửi trước là $140. {(1 + 2, 1 %)}^{5}$ triệu.

Số tiền nhận về sau 15 tháng của 180 triệu gửi sau là $180. {(1 + 0, 73 %)}^{15}$ triệu.

Suy ra tổng số tiền cả vốn lẫn lãi mà bác An thu được là

$140. {(1 + 2, 1 %)}^{5} + 180. {(1 + 0, 73 %)}^{15}$

$\approx 356, 080253$ triệu.

Suy ra số tiền lãi:

$356, 080253 - 320 = 360, 80253$

$= 36080253$ đồng.

Câu 16. Chọn kết luận đúng:

A. Hàm số $y = x^{α}$ có TXĐ D = R với mọi $a \in R$

B. Hàm số $y = x^{α}$ có TXĐ D = R với mọi $a \in Z$

C. Hàm số $y = x^{α}$ có TXĐ $D = R \ \{0\}$ với mọi $a \in Z$

D. Hàm số $y = x^{α}$ có TXĐ $D = (0; + \infty)$ với mọi $α$ không nguyên

Hiển thị đáp án

Đáp án: D

Giải thích:

Hàm số $y = x^{α}$ có TXĐ D = R với mọi $α$ nguyên dương nên A và B sai.

Hàm số $y = x^{α}$ có TXĐ $D = R \ \{0\}$ với mọi $α$ nguyên âm hoặc $α = 0$ nên C sai.

Hàm số $y = x^{α}$ có TXĐ $D = (0; + \infty)$ với mọi $α$ không nguyên nên D đúng

Câu 17. Cho các hàm số $f_{1} (x) = \sqrt{x}, f_{2} (x) = \sqrt[4]{x},$ $f_{3} (x) = x^{\frac{1}{3}}, f_{4} (x) = x^{\frac{1}{2}}$ . Trong các hàm số trên, hàm số nào có tập xác định là nửa khoảng $[0; + \infty)$

A. $f_{1} (x)$ và $f_{2} (x)$

B. $f_{1} (x)$ , $f_{2} (x)$ và $f_{3} (x)$

C. $f_{3} (x)$ và $f_{4} (x)$

D. Cả 4 hàm số trên

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $f_{1} (x)$ và $f_{2} (x)$ là hai hàm số căn bậc chẵn nên có tập xác định là $[0; + \infty)$

$f_{3} (x)$ và $f_{4} (x)$ là hai hàm số mũ với số mũ không nguyên nên có tập xác định là $(0; + \infty)$

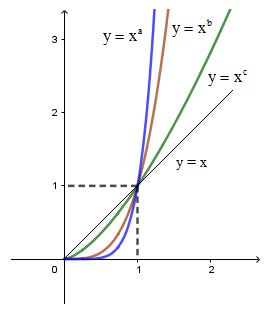
Câu 18. Cho $α, β$ là các số thực. Đồ thị các hàm số $y = x^{α}, y = x^{β}$ trên khoảng $(0; + \infty)$ được cho hình vẽ bên. Khẳng định nào sau đây là đúng?

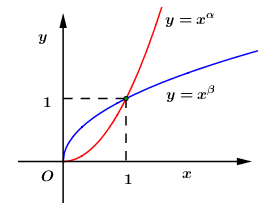
Trắc nghiệm Hàm lũy thừa có đáp án - Toán lớp 12 (ảnh 7)

A. $0 < β < 1 < α$

B. $α < 0 < 1 < β$

C. $0 < α < 1 < β$

D. $β < 0 < 1 < α$

Hiển thị đáp án

Đáp án: A

Giải thích:

Dựa vào đồ thị hàm số ta thấy hàm số $y = x^{α}$ là hàm số đồng biến trên $(0; + \infty) \Rightarrow α > 1$

Hàm số $y = x^{β}$ nghịch biến trên $(0; + \infty) \Rightarrow 0 < β < 1$

Vậy $0 < β < 1 < α$

Câu 19. Cho hàm số $y = {(x + 2)}^{- 2}$ . Hệ thức giữa y và y’’ không phụ thuộc vào x là:

A. $y'' + 2 y = 0$

B. $y'' - 6 y^{2} = 0$

C. $2 y'' - 3 y = 0$

D. ${(y'')}^{2} - 4 y = 0$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$y' = - 2 {(x + 2)}^{- 3} . (x + 2)'$

$= - 2 {(x + 2)}^{- 3}$

$y'' = - 2 (- 3) {(x + 2)}^{- 4} . (x + 2)'$

$= 6 {(x + 2)}^{- 4}$

$\Rightarrow y'' = 6 y^{2}$

$\Rightarrow y'' - 6 y^{2} = 0$

Câu 20. Trên đồ thị (C) của hàm số $y = x^{\frac{π}{2}}$ lấy điểm $M_{0}$ có hoành độ $x_{0} = 1$ . Tiếp tuyến của (C) tại điểm $M_{0}$ có phương trình là:

A. $y = \frac{π}{2} x + 1$

B. $y = \frac{π}{2} x - \frac{π}{2} + 1$

C. $y = π x - π + 1$

D. $y = - \frac{π}{2} x + \frac{π}{2} + 1$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $y' = \frac{π}{2} x^{\frac{π}{2} - 1}$

$\Rightarrow y' (1) = \frac{π}{2}$

Với $x_{0} = 1$ thì $y_{0} = 1^{\frac{π}{2}} = 1$

Vậy phương trình tiếp tuyến của đồ thị hàm số tại điểm $M_{0}$ là:

$y = \frac{π}{2} (x - 1) + 1$

$= \frac{π}{2} x - \frac{π}{2} + 1$

Câu 21. Tìm tập xác định D của hàm số $y = {(x^{3} - 6 x^{2} + 11 x - 6)}^{- 2}$

A. $D = R$

B. $D = R \ \{1; 2; 3\}$

C. $D = (1; 2) \cup (3; + \infty)$

D. $D = (- \infty; 1) \cup (2; 3)$

Hiển thị đáp án

Đáp án: B

Giải thích:

Đây là hàm số với số mũ nguyên âm nên điều kiện là

$x^{3} - 6 x^{2} + 11 x - 6 \neq 0$

$\Leftrightarrow x \in R \ {1; 2; 3}$

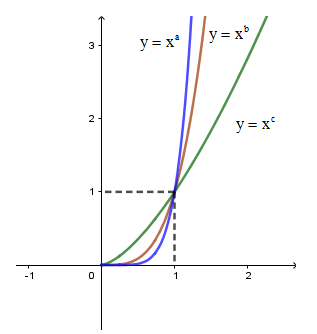
Câu 22. Cho đồ thị của ba hàm số $y = x^{a}; y = x^{b}; y = x^{c}$ trên khoảng $(0; + \infty)$ trên cùng một hệ trục toạ độ như hình vẽ bên. Mệnh đề nào sau đây đúng?

A. $c, b < a < 0$

B. $0, c < b < a < 1$

C. $1 < c < b < a$

D. $0 < a < b < c < 1$

Trắc nghiệm Hàm lũy thừa có đáp án - Toán lớp 12 (ảnh 8)

Hiển thị đáp án

Đáp án: C

Giải thích:

Trắc nghiệm Hàm lũy thừa có đáp án - Toán lớp 12 (ảnh 9)

Từ đồ thị hàm số ta thấy:

- Với $0 < x < 1$ thì $x^{a} < x^{b} < x^{c} < x^{1}$

$\Leftrightarrow a > b > c > 1$

- Với x > 1 thì $x < x^{c} < x^{b} < x^{a}$

$\Leftrightarrow a > b > c > 1$

Vậy $1 < c < b < a$

Câu 23. Cho hàm số $y = x^{α}$ . Nếu $α = 1$ thì đồ thị hàm số là:

A. Đường thẳng

B. Đường tròn

C. Đường elip

D. Đường cong

Hiển thị đáp án

Đáp án: A

Giải thích:

Với $α = 1$ thì $y = x^{1} = x$ nên đồ thị hàm số là đường thẳng

Câu 24. Cho hàm số $y = x^{π}$ . Tính $y'' (1)$

A. $y'' (1) = 0$

B. $y'' (1) = π \ln π$

C. $y'' (1) = π (π - 1)$

D. $y'' (1) = \ln^{2} π$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $y' = π x^{π - 1}$

$\Rightarrow y'' = π (π - 1) x^{π - 2}$ do đó $y'' (1) = π (π - 1)$

Câu 25. Biết thể tích khí $C O_{2}$ năm 1998 là $V (m^{3})$ . 10 năm tiếp theo, mỗi năm thể tích $C O_{2}$ tăng m%, 10 năm tiếp nữa, thể tích $C O_{2}$ mỗi năm tăng n%. Tính thể tích $C O_{2}$ năm 2018?

A. $V \frac{{(100 + m)}^{10} {(100 + n)}^{10}}{10^{40}}$

B. $V \frac{{(100 + m)}^{10} {(100 + n)}^{8}}{10^{36}}$

C. $V \frac{{(100 + m)}^{10} {(100 + n)}^{8}}{10^{20}}$

D. $V \frac{{(100 + m)}^{10} {(100 + n)}^{10}}{10^{36}}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Thể tích khí $C O_{2}$ năm 2008 là: $V_{2008} = V {(1 + \frac{m}{100})}^{10}$

Thể tích khí $C O_{2}$ năm 2018 là:

$V_{2008} = V_{2008} {(1 + \frac{n}{100})}^{10}$

$= V {(1 + \frac{m}{100})}^{10} {(1 + \frac{n}{100})}^{10}$

$= V \frac{{(100 + m)}^{10} {(100 + n)}^{10}}{10^{40}}$

Câu 26. Tính tổng các nghiệm của phương trình Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

A. 7.

B. 25.

C. 73.

D. 337.

Hiển thị đáp án

Đáp án: A

Giải thích:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Tổng hai nghiệm : 81 + 256 = 337

Câu 27: Cho 2 hàm số f(x) = x² và g(x) = x^1/2 . Biết rằng α > 0, f(α) < g(α). Khẳng định nào sau đây là đúng?

A. 0 < α < 1/2

B. 0 < α < 1

C. 1/2 < α < 2

D. α > 1

Hiển thị đáp án

Đáp án: A

Giải thích: Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 28: Tìm các điểm cực trị của hàm số

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

A. x=1.

B. x=2.

C. x=1 và x=-2

D. x=2 và x=-1.

Hiển thị đáp án

Đáp án: A

Giải thích: Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

y'= 0 <=> x² + x - 2 = 0 <=> x = -2 (loại) hoặc x = 1

y' đổi dấu khi đi qua điểm x = 1 nên hàm số có một điểm cực trị là x = 1

Câu 29. Tìm các điểm cực trị của hàm số

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

A. x = 2.

B. x= 3/2

C. x = 6.

D. x = 4.

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

y’ đổi dấu khi đi qua điểm x = 3/2 nên hàm số có một điểm cực trị là x = 3/2

Câu 30. Tìm các giá trị lớn nhất và nhỏ nhất của hàm số Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Hiển thị đáp án

Đáp án: C

Giải thích:

Tập xác định D = [0; 1]

Ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

y(0) = y(1) = 1; y(1/2) = ∜8. Từ đó max y = y(1/2) = ∜8, min y = y(0) = 1

Câu 31. Tìm các giá trị lớn nhất và nhỏ nhất của hàm số y = x^2/3(20 - x) trên đoạn [1; 10]

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Hiển thị đáp án

Đáp án: D

Giải thích: Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

y' = 0 <=> x = 8

Ta có: y(1) = 19, y(8) = 48, y(10) = 10^5/3 ≈ 46,6 > 19

Từ đó:

Câu 32. Hàm số nào dưới đây không là hàm số lũy thừa?

A. $y = \frac{1}{x^{4}}$

B. $y = x^{- \sqrt{2}}$

C. $y = e^{x}$

D. $y = x^{π}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Các hàm số ở mỗi đáp án A, B, D đều là hàm số lũy thừa.

Câu 33. Chọn kết luận đúng

A. Hàm số $y = x^{α}$ có TXĐ D = R với mọi $a \in R$

B. Hàm số $y = x^{α}$ có TXĐ D = R với mọi $a \in Z$

C. Hàm số $y = x^{α}$ có TXĐ $D = R \ \{0\}$ với mọi $a \in Z$

D. Hàm số $y = a^{α}$ có TXĐ $D = \{0; + \infty\}$ với mọi $α$ không nguyên

Hiển thị đáp án

Đáp án: D

Giải thích:

Hàm số $y = x^{α}$ có TXĐ D = R với mọi $α$ nguyên dương nên A và B sai.

Hàm số $y = x^{α}$ có TXĐ $D = R \ \{0\}$ với mọi $α$ nguyên âm hoặc $α = 0$ nên C sai.

Hàm số $y = x^{α}$ có TXĐ $D = \{0; + \infty\}$ với mọi $α$ không nguyên nên D đúng

Câu 34.

Hàm số nào dưới đây có tập xác định không phải là R?

A. $y = {(x^{2} + 1)}^{\frac{1}{2}}$

B. $y = \sqrt{x^{2}}$

C. $y = \frac{x}{x - 1}$

D. $y = \sqrt[3]{x}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Hàm số $y = {(x^{2} + 1)}^{\frac{1}{2}}$ có điều kiện xác định $x^{2} + 1 > 0$ (luôn đúng) nên TXĐ: D = R

Hàm số $y = \sqrt{x^{2}}$ có điều kiện xác định $x^{2} \geq 0$ (luôn đúng) nên TXĐ: D = R

Hàm số $y = \frac{x}{x - 1}$ có điều kiện xác định $x - 1 \neq 0 \Leftrightarrow x \neq 1$ nên TXĐ: $D = R \ \{1\}$

Hàm số $y = \sqrt[3]{x}$ xác định với mọi x nên TXĐ: D = R

Câu 35. Hàm số nào có tập xác định là D = R.

A. $y = x^{5}$

B. $y = x^{- 1}$

C. $y = x^{\sqrt{2}}$

D. $y = {(x^{\sqrt{2}})}^{2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Câu 36. Cho hàm số $y = x^{α}$ . Nếu $α = 1$ thì đồ thị hàm số là:

A. Đường thẳng

B. Đường tròn

C. Đường elip

D. Đường cong

Hiển thị đáp án

Đáp án: A

Giải thích:

Với $α = 1$ thì $y = x^{1} = x$ nên đồ thị hàm số là đường thẳng

Câu 37. Đồ thị hàm số $y = x^{α}$ là đường thẳng khi:

A. $α > 0$

B. $α = 1$

C. $α = - 1$

D. $α = 0 h o ặ c α = 1$

Hiển thị đáp án

Đáp án: D

Giải thích:

Khi $α = 0$ thì y = 1 nên đồ thị hàm số là đường thẳng.

Khi $α = 1$ thì y = x nên đồ thị hàm số là đường thẳng

Câu 38. Cho hàm số $y = x^{α}$ có đồ thị như hình dưới. Điều kiện của $α$ là

A. $α > 0$

B. $α = 0$

C. $α < 0$

D. $α < 1$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có dáng đồ thị hàm số lũy thừa $y = x^{α}$

Quan sát hình vẽ các dáng đồ thị của hàm số lũy thừa ta thấy điều kiện của $α$ ứng với các đồ thị bài cho là $α < 0$

Câu 39. Một người gửi tiết kiệm vào ngân hàng số tiền A đồng, lãi suất mỗi tháng là r, gửi theo hình thức lãi kép không kì hạn. Công thức tính số tiền cả vốn lẫn lãi mà người đó nhận được sau N kì hạn là:

A. $T = A {(1 + r)}^{N}$

B. $T = r {(1 + A)}^{N}$

C. $T = A {(1 + N)}^{r}$

D. $T = N {(1 + A)}^{r}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Công thức tính số tiền cả vốn lẫn lãi mà người đó nhận được sau N kì hạn là: $T = A {(1 + r)}^{N}$

Câu 40. Chọn kết luận đúng

A. Hàm số $y = x^{α}, (a \neq 0)$ đồng biến trên $(0; + \infty)$ nếu $α < 0$

B. Hàm số $y = x^{α}, (a \neq 0)$ nghịch biến trên $(0; + \infty)$ nếu $α < 0$

C. Hàm số $y = x^{α}, (a \neq 0)$ đồng biến trên $(0; + \infty)$ nếu $α \neq 0$

D. Hàm số $y = x^{α}, (a \neq 0)$ nghịch biến trên $(0; + \infty)$ nếu $0 < α < 1$

Hiển thị đáp án

Đáp án: B

Hàm số $y = x^{α}, (a \neq 0)$ đồng biến trên $(0; + \infty)$ nếu $α > 0$ nên A và C sai.

Hàm số $y = x^{α}, (a \neq 0)$ nghịch biến trên $(0; + \infty)$ nếu $α < 0$ nên B đúng, D sai.

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Logarit có đáp án

Trắc nghiệm Hàm số mũ. Hàm số Logarit có đáp án

Trắc nghiệm Phương trình mũ và phương trình Logarit có đáp án

Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án

Trắc nghiệm Ôn tập Chương 2 có đáp án

1 4,377 22/12/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3